动画: 快速排序 | 如何求第 K 大元素？

Posted 2021-05-02 小鹿动画学编程

点击蓝色 “小鹿动画学编程” 关注我哦!

加个 “星标” ，每天一篇动画喂饱你！

作者 |  小鹿

来源 |  小鹿动画学编程

写在前边

我们有这么一个需求，老板和我们说，要求我们做这么一个员工系统，公司员工的相关信息和为公司的贡献值都会在这个系统进行记录，每到月底评功轮赏的时候，根据员工这一个月的表现进行奖罚。你可能会说，这还不好做吗？增删改查，然后直接按照贡献值从大到小排序就好了。

别着急，还有一个需求就是公司每个月都会进行抽奖福利，抽奖的方式是，老板随机抽取贡献值为第 K 大的贡献值的员工送出福利一份，共选取 n 位，而不是评功论赏了，如果让你实现一个系统，你该如何实现呢？

如果你学完今天的快速排序，就很轻松的解决老板给你分配的任务啦。

思维导图

1

什么是快速排序？

顾名思义，快速排序，那肯定快呀，那到底有多快呢？快不过三秒？

假如我们已经接过老板在数据库给我们取出的本月每个员工的信息，我们单独筛选出贡献值，如下数据。

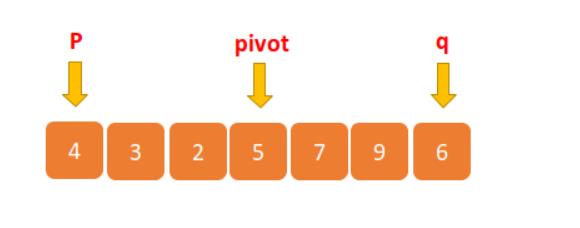
为了能够更加清晰的讲解，我们对一些用到的特殊数据进行标识一下。

如上数据，我们从 p 到 q 随机找一个元素作为区分点（pivot），什么是区分点？稍后我们解释。我们就选择最后一个数据 5 吧，然后我们以 5 为区分点，然后从 p 开始遍历元素，如果当前遍历的元素小于 5，我们就放在 5 的前边，如果当前遍历的元素大于 5，我们就放在 5 的后边，最后的结果如下：

看了上边的一顿操作，我们也明白了为什么 5 是区分点了。上边的数据也没有从小到大呀？别着急，重点来了。

我们是整体数据按照 5 为区分点进行重新排列数据的，如果我们使用同样的方式分别对 5 左边和 5 右边的数据分别进行这种方式的划分，直到划分到区间为 1 为止，是不是数据就会变的有序了？没错，这就是我们所说的快速排序。

有小伙伴会问到，这多麻烦，也快不过三秒呀？我们后边会有性能分析的，到时候就知道快排比我们之前讲的冒泡、插入有多快了。

2

动画实现

3

快速排序的原理

虽然我们上边笼统的分析了快速排序的基本过程，但是其中有两个中要的知识点，快速排序的过程用到了递归和分治思想，我们分开进行分开讲解。

1、

递归

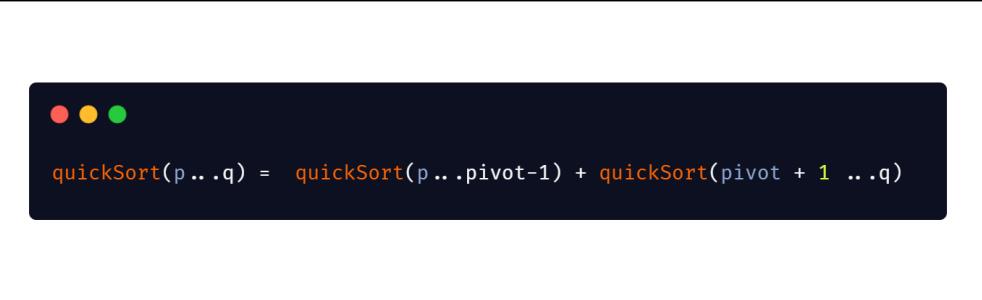
首先看一下快速排序的递推公式，我们不断的将大区间分割成小区间，然后对小区间再次进行分割。

我们可以总结出以上的递推公式。

因为我们不断的将大区间分成小区间，然后一直分下去，不对，一直分总有一个尽头的，所以这也是递归的终止条件。当满足这个条件时，就不再继续往下进行递归，那么快速排序的递归条件是什么呢？上边也说到了，当区间只剩一个数据的时候，我们不再进行划分，所以递归条件为：

p >= q

递归的代码实现：

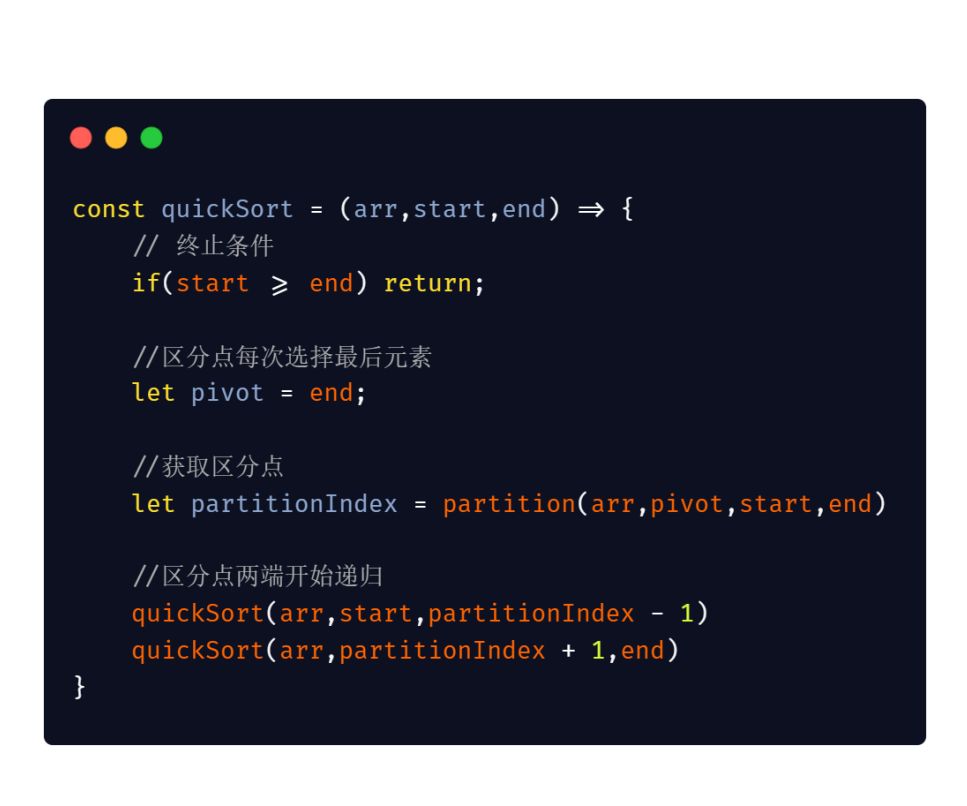
2、

分治思想

我们之所以将大问题不断的分成小问题，就是用到的分治思想，分而治之，将分解的小问题解决了，大问题自然而然就会得到解决。

最关键的是快速排序中有一个分区函数 partition，分区函数的作用就是随机找到一个区分点 pivot，然后对数据进行分区，该函数会返回分区后 pivot 的下标。

我们好奇的是如何进行分区的？我们需要用到一个分区函数 partition，我们想到最简单的方法可能就是小于 pivot 的元素放到数组 a 中，大于 pivot 的元素放到数组 b 中，然后合并 a 和 b，完成分区。

如果我们不考虑空间上的消耗的话，这样写没毛病的。但是，为了考虑到空间上的消耗，也就是我们希望空间复杂度是 O(1)，不得不让分区函数占用少的内存空间，我们需要在原数组中完成分区，而不是另外开辟新的空间。

这个过程我们单纯的想是很难想出来的，而且非常有技巧性，所以我们一起来看一下。我们还是以上边的数据为例，从 p 开始遍历元素，分别和 pivot 区分点元素进行比较，如果小于区分点元素，我们就进行交换，如果大于区分点元素，我们就不进行交换，我们具体来看一下动画的实现。

4

快速排序的性能

我们知道快速排序的整个实现过程了，下面我们来分析一下快速排序的性能如何，不是你说很快嘛？能快过三秒吗？

时间复杂度

我们先来看时间复杂度，快速排序时间复杂度的计算是分区操作的时间加上合并的时间，快速的时间复杂度为 O(nlogn)。这是理想情况下，为什么呢？因为我们随机选择区分点不可能每次都能将数据一分为二。

还有一种极端的情况就是，如果原数据是一组有序数据，如果每次都要选择最后一个元素为区分点，大约需要进行 n 次操作，每次遍历 n/2 个元素，所以时间复杂度就会推化成 O(n²)。

虽然存在这种情况，但是这种情况的概率是极低的，而且我们有方法可以将这种方法降到最低，在基础环节，我们不多啰嗦。快速排序大部分情况下的平均时间复杂度为 O(nlogn)。

空间复杂度

我们上边也特别强调了，我们分区函数只需在原数组中进行分区操作就可以完成，不需要开辟额外的内存空间，所以空间复杂度为 O(1)。

快速排序无论是时间效率还是空间效率，足以比我们之前讲的冒泡排序和插入排序要效率高的多，在一些排序函数的框架源码中，我们也会使用到快速排序，所以快排的应用还是非常广泛的，所谓快不过三秒“真男人”。

5

代码实现

JavaScript 版本

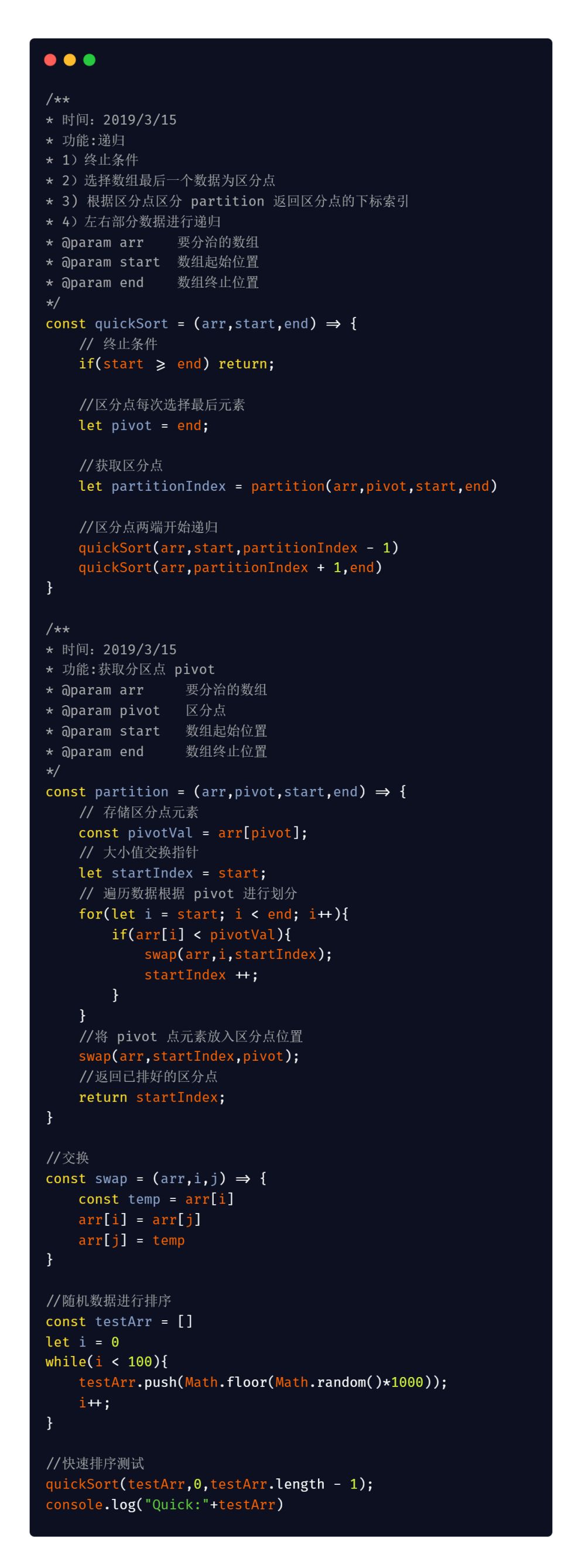
Java 版本

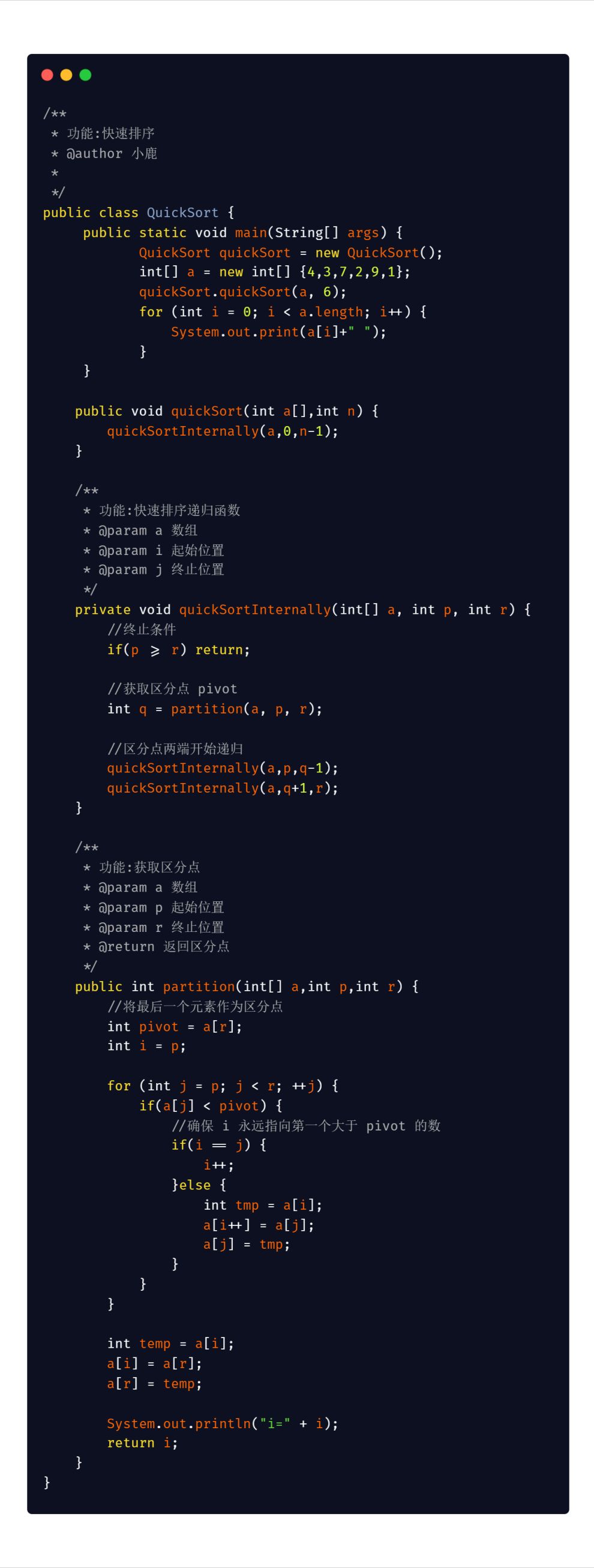
6

小结

我们回到文章开头的问题上，我们有一组员工的贡献值数据，我们要随机选取第 K 大的贡献值的员工发放奖品，如何实现呢？

你可能会问，今天讲的快速排序和这个问题有什么直接的挂钩呢？表面看起来并没有什么挂钩，而这个问题的解决是对快速排序代码的一个变体，稍微改动一下，就可以轻松解决上述问题。

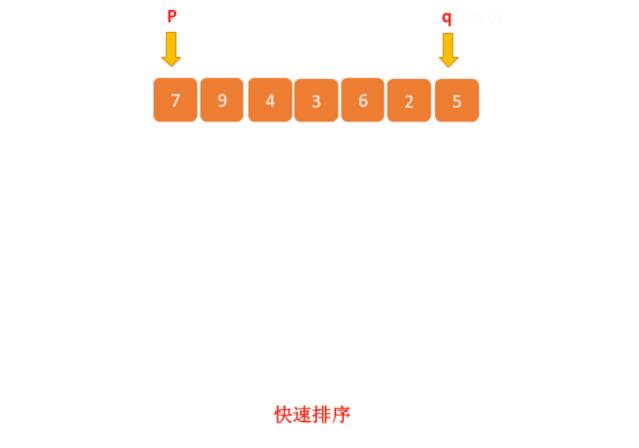
比如几位员工的贡献值如下：7、9、4、3、6、2、5 。第 4 大元素就是 5，那就恭喜贡献值为 5 的员工获得奖金一份，虽然实际情况下不太可能用这种方式发奖品，这里我们只是拿这个例子来讲。

我们将上边的数据像快速排序一样分为三部分，分别为 [0,p-1] p [p,q]，这是已经完成分区函数的数据，因为我们从 0 开始的，然后判断当前的 p + 1 是否等于 K？如果等于 K ，那么数组中下标为 p 的元素就是第 K 大数据。

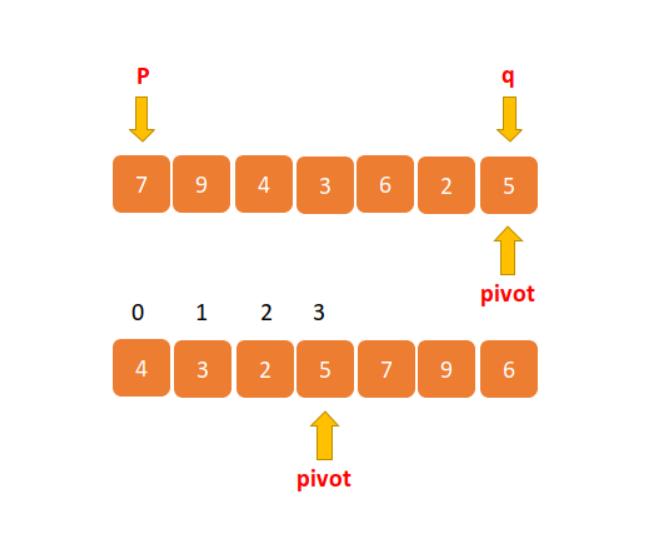
如上图的 5 就是第四大数据，但是它在数组中的下标为 3，所以需要加 1。

推荐阅读：

1、

2、

3、

「小鹿动画学编程」用动画的形式和你分享技术！

在看和转发

都会带来更多好运