面试官，不要再问我快速排序了！

Posted 2021-05-02 Leron爱解码

前言

面试的时候让手写快排算法，作为学习小能手早就把书上的代码背的熟透了，咔咔一顿写，完事了觉得这次稳了。没想到！！！面试官突施冷箭，这种写法有问题吗，还能优化吗？我心里一万个黑人问号，书上的代码还能有问题，快排还能优化。一首凉凉送给自己，回家等通知了。

面试时越简单的问题，一般就是隐藏着比较大的坑，一般都是需要将问题扩展的。书上的代码肯定是没有问题的，但是没有真正理解快速排序的精髓，没有清楚快排的优缺点和扩展优化，距离面试要求还是有点距离的。

正文

快速排序使用分治法将序列分成两个较大和较小的子序列，然后递归的排序两个子序列。

1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot），

2. 分割：所有比基准值小的元素放在基准值的左边，所有比基准值大的元素放在基准值的右边，分割成两个子序列

3. 递归排序子序列：递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。

分治的思想

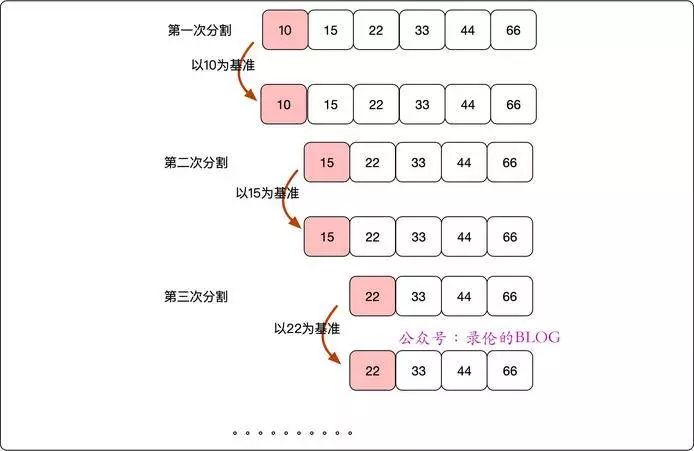
如图所示，在分治的思想下，选择最左元素为基准点，序列每次都被拆分成两个子序列，直到不可拆分为止。每次分割都会产生2的指数个序列，大约需要logN次分割就可以分割所有的节点。所以时间复杂度O(NlogN)

基本算法设计

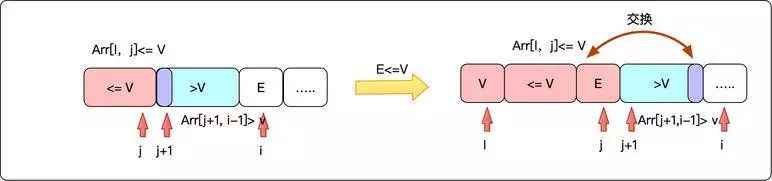
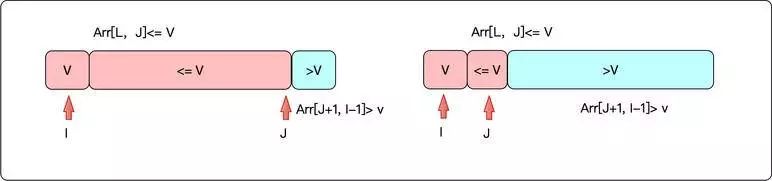
以最左元素Arr[l]=V为基准点，序列分为<=V的[l,j]区间和>V的[l+1,i-1]区间。如果第i个元素小于V，则将Arr[j+1]和Arr[i]交换.

快排基本算法

    public void sort(int[] args) {
        if (args == null || args.length <= 0) {
            return;
        }
        sort(args, 0, args.length - 1);
    }

    private void sort(int[] args, int l, int r) {
        if (l >= r) {
            return;
        }
        int m = partition(args, l, r);
        sort(args, l, m - 1);
        sort(args, m + 1, r);
    }

    private int partition(int[] args, int l, int r) {
        //返回p,使得arr[l...p-1]<arr[p]; arr[p+1...r]>arr[p]
        int j = l;
        int target = args[l];
        for (int i = l + 1; i <= r; i++) {
            // 交换后保证 arr[l, j] <= target
            if (args[i] <= target) {
                swap(args, j + 1, i);
                j++;
            }
        }
        swap(args, j, l);
        return j;
    }

基准元素的选择

基本有序的序列对于快速排序是最坏的场景，也是上文中面试官提到的其中一个优化点。因为每次只分割出一个基准点，需要N次分割，时间复杂度为O（N^2）.

快排最坏的情况

改进为：随机选择一个元素作为基准点，而不是选择最左的元素. 对于基本有序的序列，因为随机选择，每次选中最小的元素作为基准元素的概率为1/N，出现最坏的情况概率已经很小了：1/(N*N)，几乎不会发生。

    private int partition(int[] args, int l, int r) {
        Random random = new Random();
        swap(args, l, l + random.nextInt(r - l));
        int target = args[l]; //设定最左边的元素为pivot值
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (args[i] <= target) {
                swap(args, i, j + 1);
                j++;
            }
        }
        swap(args, l, j);
        return j;
    }

重复元素导致的最坏情况

细心的同学可能看到上述的算法把重复的情况归类到小于V的序列中。当序列中有很多重复数据的时候，一次分割为两个极不平衡的序列，导致算法复杂度退化到O(n^2).

重复的情况

二路快排

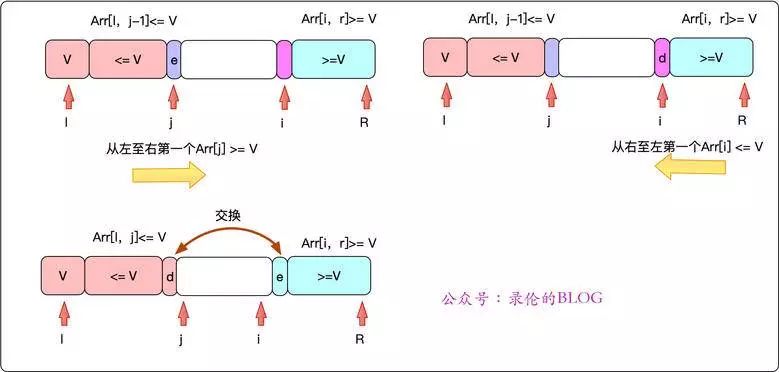
通过左右两个指针i，j将整个序列均衡的分为>=V和<=V两个部分.从左至右找到第一个大于基准值的j，从右至左找到第一个小于基准值的i，交换i和j的值，然后i--，j++。

二路快排

    private int partition(int[] args, int l, int r) {
        //返回p,使得arr[l...p-1]<=arr[p]; arr[p+1...r]>=arr[p]
        int j = l + 1, i = r;
        Random random = new Random();
        swap(args, l, l + random.nextInt(r - l));
        int target = args[l];
        while (true) {
            while (j <= r && args[j] < target) {
                j++;
            }
            while (i >= l + 1 && args[i] > target) {
                i--;
            }
            if (j > i) {
                break;
            }
            swap(args, i, j);
            j++;
            i--;
        }
        swap(args, i, l);
        return i;
    }

三路快排

当序列中有大量的重复元素，二路排序虽然会均衡的分配到两个序列中，但是重复元素仍然参与到分割序列中，带来无谓的性能损耗。所以三路快排将整个序列分为大于V和小于V，等于V三个部分：Arr[l，lt]小于V；Arr[lt+1，i-1]==V；Arr[gt，r]大于V。我们只关心小于V和大于V的子序列，递归的分割这些子序列。

三路快排

三路快排

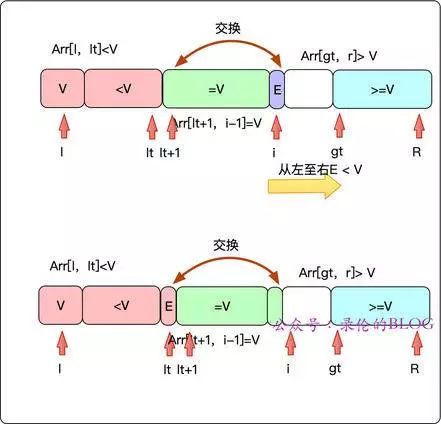
    public void sort(int[] args, int l, int r) {
        if (l >= r) {
            return;
        }

        int target = args[l];
        int lt = l, gt = r + 1, i = l + 1;
        while (i < gt) {
            if (args[i] < target) {
                swap(args, i, lt + 1);
                lt++;
                i++;
            } else if (args[i] > target) {
                swap(args, i, gt - 1);
                gt--;
            } else {
                i++;
            }
        }
        swap(args, l, lt);

        sort(args, l, lt - 1);
        sort(args, gt, r);
    }

总结

快排算法是经典的排序算法，面试中经常要求手写出来，真正理解算法的精髓，写出来是很简单的。算法的优缺点要明确，改进的原因和策略也要掌握。在面试中才不会手足无措，泰然处之。

更多原创好文，请关注「录伦的BLOG」