时间序列基本概念
Posted 私募工场
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了时间序列基本概念相关的知识，希望对你有一定的参考价值。
关键词：专业配置 领航私募 精雕细琢 匠心服务 私募FOF 独立客观
私募工场：私募证券投资领域最权威、最独立、最专业化自媒体
果果微信：guo5_guoguo
投顾净值：506743560@qq.com
本文转自SAS知识 （ID: SASAdvisor），摘自《深入解析SAS — 数据处理、分析优化与商业应用 》
将讨论如何建立、识别、拟合和检验时间序列模型，并结合SAS软件中的TIMESERIES过程、ARIMA过程、FORECAST过程、AUTOREG过程及ESM过程介绍如何对平稳时间序列和非平稳时间序列进行建模和预测。
在经济学、工程学、自然科学（特别是地球物理学和气象学）和社会科学等领域，被研究的对象在其发展过程中，由于受到各种偶然因素的影响，往往表现出某种随机性，它们常常被记录成一系列随时间而变化的数据序列。我们把按时间顺序生成的、等时间间隔的这种数据序列称为时间序列。
很多数据都是以时间序列的形式出现的，比如：某种产品的月度需求量、公路事故的周度数量、某化工过程每小时的产出量，等等。时间序列的一个本质特征就是相邻观测值之间具有相互依赖性，这种依赖特征具有很大的实用价值。时间序列分析就是对这种依赖性进行分析的技术。
后面我们会在系列文章中将讨论如何建立、识别、拟合和检验时间序列模型，并结合SAS软件中的TIMESERIES过程、ARIMA过程、FORECAST过程、AUTOREG过程及ESM过程介绍如何对平稳时间序列和非平稳时间序列进行建模和预测。
为了便于后面具体时间序列分析方法的介绍，本节中先介绍基本概念。
了解时间序列
如果一个时间序列中的时间是连续的，那么该时间序列就是连续的。如果时间是离散的，那么该时间序列就是离散的。因此，一个离散时间序列在时刻
得到的观测值就可以记为
。在本章中，仅仅考虑离散的时间序列。请注意，时间序列中的观测值是按照固定的时间间隔取得的，时间间隔可以是秒、分钟、小时、天等。
如果一个时间序列的取值取决于某些数学函数，如
，则称该时间序列是确定性的。如果一个时间序列的未来值只能用概率分布的形式来描述，则表示该时间序列不具有确定性，称为统计时间序列。时间序列图，也称为时序图，就是一个二维坐标图，私募工场ID：Funds-Works，老板娘微信guo5_guoguo，横坐标表示时间，纵坐标表示序列取值。时序图可以直观地帮助我们了解时间序列的一些基本分布特征。比如，图17.1就是一个时序图，该图展示了从1990年1月到2013年12月美国国内航线旅客数量（源数据可以从http://www.transtats.bts.gov网站上下载得到），每个圆圈代表着一个观测值。尽管在这个序列中有明确的上下波动形状，但是要想准确地预测下一个时段的值仍然是不可能的。这就是本章所关注的统计时间序列。
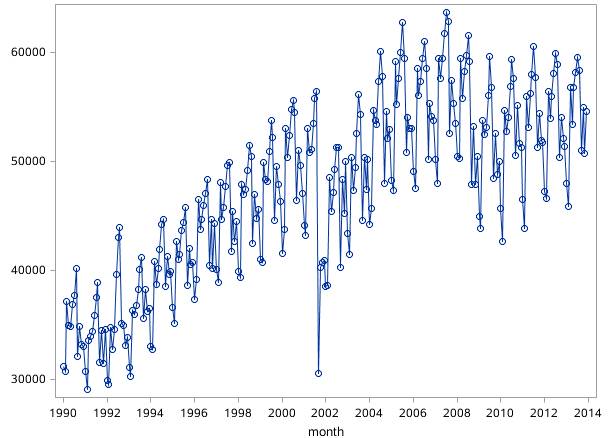
图17.1从1990年1月至2013年12月美国国内航线旅客数量
如果要考察美国国内航线的旅客数量，很明显是要考虑时间t的，所以可以把旅客数量表示为Y(t)。对每一个确定的时间Y(t0)，都是一个随机变量。理论上t的取值范围是(-∞, +∞)为无穷多个依赖于时间t的随机变量，我们称之为随机过程。
对随机过程Y(t)的值进行一次观测和记录，就可以得到在本章开始时所提到的一系列随时间而变化的数据序列，实际上该序列已经是一个确定（而非随机的）常规意义的函数Y(t)，我们称之为随机过程的Y(t)一个现实。当随机过程Y(t)的现实的时间参数为离散的，并且时间取值的间隔相等时，那么该现实就是一个时间序列在美国国内航线旅客数量的示例中，如果我们仅仅关心时间t为月份的情况，我们所记录到Y(t)的在1990年1月到2013年12月的一系列值，就是一个表示美国国内航线每个月份旅客数量的时间序列。
时间序列分析的目的是选择恰当的技术和方法，建立合适的随机过程模型，由时间序列的当前值和过去值对未来值进行预测，并解释和描述外部因素和异常干扰对于时间序列的影响，进而通过设计有效的控制方法对时间序列进行控制。
时间序列的数字特征
时间序列分析方法是根据时间序列观测间的依赖性特点，来建立模型，所以对该依赖性特征的识别很重要。用图形的方法可以在一定程度上识别时间序列的特征，且很直观。来看几组时序图，如图17.2至图17.4所示。
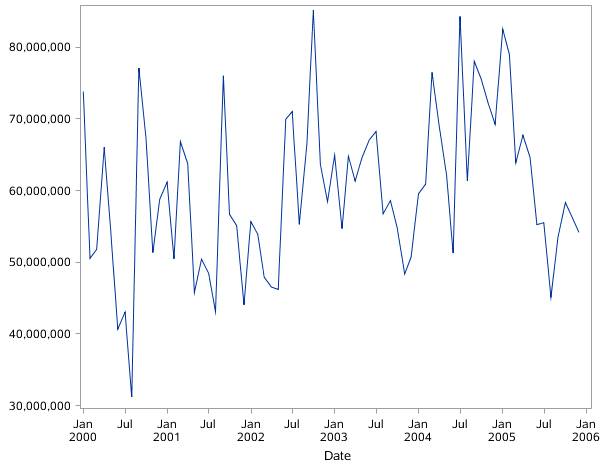
图17.2时间序列1-因特尔公司股票月度成交量
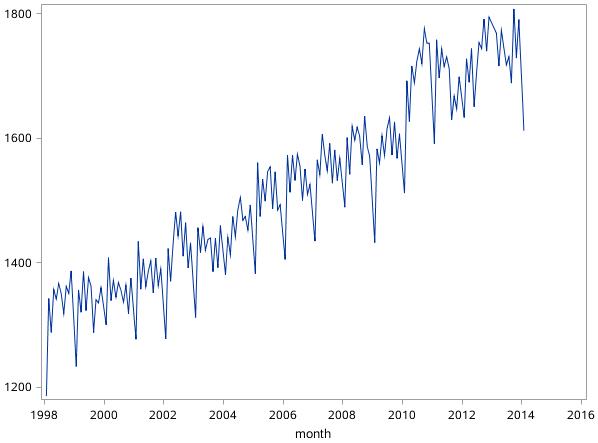
图17.3时间序列2-国内天然原油月度产量
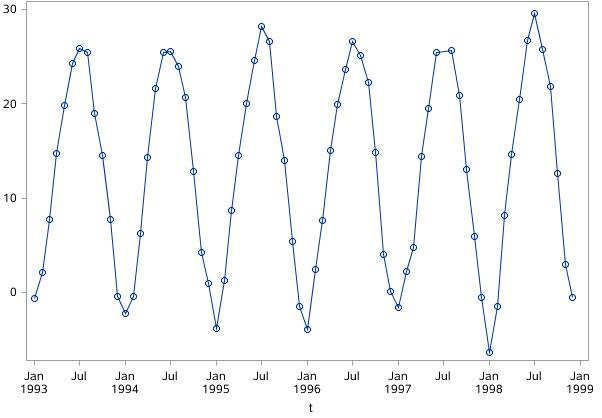
图17.4时间序列3-北京月度平均气温
在这些图形中：
时间序列1：该时间序列变化平稳，无明显的周期特征，无明显的趋势；
时间序列2：该时间序列有明显的增长趋势；
时间序列3：该时间序列变化平稳，但有明显的周期特征。
但是图形识别不是量化的标准，所以往往不够准确。
时间序列的数字特征是时间序列的重要统计特征，也是量化识别时间序列的重要依据。
也就是说，具有不同分布的时间序列可以有相同的均值函数、自协方差函数和自相关函数。但对于大量的实际应用而言，通过以上数字特征来掌握时间序列的统计特性已经足够了。时间序列分析正是通过分析时间序列的数字特征来分析时间序列的行为和特点的。
满足以下条件的时间序列称为平稳时间序列
换句话说，平稳时间序列的均值是常数，方差也是常数，序列没有明显的变化趋势，观测值始终围绕在同一个水平线上下波动。图17.2符合平稳时间序列的特征，图17.3是非平稳时间序列。
满足以下条件的时间序列称为白噪声序列，也称为纯随机序列：
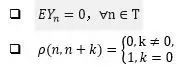
从定义来看，白噪声序列是平稳时间序列中的特例。由于白噪声序列不同时刻的取值相互独立（从自相关函数判断），因此从已知的观测值不能对未来进行推断和预测，所以白噪声序列不能用来建立模型。图17.5是一个白噪声序列的时序图。
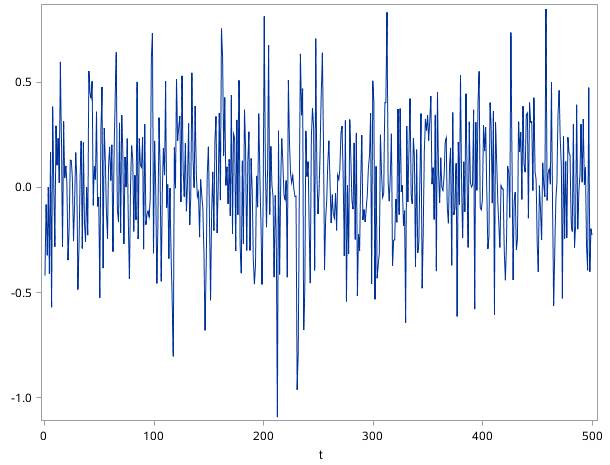
图17.5白噪声序列
平稳时间序列和白噪声序列在后面的讨论中将经常出现。
在实际应用中，由于信息的缺乏，我们往往不可能知道时间序列理论均值和自相关函数，但是通过样本，是可以计算样本的均值和样本的自相关函数的。
样本自相关函数可以作为时间序列自相关函数的一个估计。
常见平稳和非平稳模型
前面说过，时间序列是随机过程的一个现实。我们对时间序列进行分析，就是希望根据时间序列的特征，找到可以刻画这个时间序列的随机过程。
接下来，将介绍描述时间序列的一类重要随机模型：平稳模型。平稳模型会假设随机过程保持概率特征上的统计均衡，其均值和方差不随时间而改变，即变化都是在一个固定的均值水平上，具有固定的方差。这类模型非常适合用来对平稳时间序列进行刻画。
1. 算子
为了便于对平稳模型和非平稳模型进行介绍，
2. 自回归模型
在描述某类实际中出现的时间序列时，一种特别有用的随机模型是自回归模型。在该模型中，随机过程的当前值被表达为由有限的过程先前值的线性组合和一个干扰（白噪声）
构成，其形式如下：
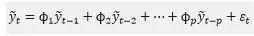
该等式表示的随机过程称为p阶自回归过程，简称AR（p）过程，其中，
，为时间序列的均值。称其为自回归是因为这是从线性回归中发展而来的，但是，这里不再是用x预测y，而是用y自身的历史值来预测y，也称AR模型。如果引入后移算子B，那么由上面的等式可以很容易地推导出p阶自回归算子
，
从而，p阶AR模型就可以简记为
需要特别说明的是，1阶AR模型，记为AR（1），也可以表示为
考虑简单的1阶AR模型，经过m次替换后，即令，在右边可以得到
（1）自相关函数
由特征方程
根的性质，可知一个平稳的自回归过程的自相关函数的变化趋势是由指数衰减和正弦波振荡衰减构成的。这是我们根据自相关函数判断序列平稳性的理论基础。
（2）自回归参数的表示
（3）偏自相关函数
在分析一个时间序列时，最初我们可能不知道适合于观测序列的AR过程的具体阶数，即p的取值，要采用类似于在多元回归中的方法去确定自变量的个数。其实，这时可以参考偏自相关函数。
偏自相关函数是基于以下事实的一种描述手段：只要一个AR（p）过程具有无限延生的自相关函数，那么，就可有自相关函数的p个非零函数来描述自身的特性。若用
表示k阶差分方程回归表达式中的第j个系数，
就是最后一个系数。由此可得到Yule-Walker方程，记为
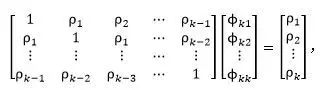
对k=1，2，3，…，依次求解方程，可以得到
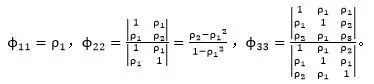
对于任何平稳过程，都可以由上述Yule-Walker方程定义偏自相关函数
，当然也都是作为过程自相关函数pk的函数。并且，对于AR（p）过程，对于所有的k>p，有=0，该特征均适合于描述p阶AR过程。
因此，在求偏自相关函数的估计时，可以顺次拟合阶数为1，2，3，…的自回归方程，在每阶段的拟合中挑出最后一个系数，得到估计
…。
Quenouille证明了：在p阶AR过程的假设之下，阶数大于或者等于p+1的偏自相关估计值近似服从均值为零、方差为1/n的独立正态分布，其中n为观测个数。这一论断可以作为判断AR模型阶数p的取值依据之一。
3. 移动平均模型
（1）自相关函数
可以看到，对于MA（q）的过程，当延迟阶数超过q时，过程的自相关函数为0。换言之，移动平均过程的自相关函数具有超出q步延迟的截尾性。
（2）移动平均参数的表示
由上述自相关函数的推导结果可知，若
为已知，则由q个方程就可以解出参数
，然而，与自回归过程线性的Yule-Wallker方程不同，这里的q个方程为非线性方程。除了q=1的简单情形，其余情形只能用迭代法求解。
（3）偏自相关函数
对于高阶的MA过程，偏自相关函数的严格表达式是很复杂的，但是可以证明偏自相关函数被衰减指数和（或）衰减正弦波控制。
（4）自回归过程和移动平均过程的对偶性
平稳的AR过程具有在某阶之后全为零的偏自相关函数，但是它的自相关函数是无限延伸的，且由衰减指数或衰减正弦波混合生成；相反的，有限的MA过程具有在某阶之后全为零的自相关函数，但由于它等价于一个无限的AR过程，因此其偏自相关函数将无限延伸，且被衰减指数和（或）衰减正弦波控制。
4. 自回归移动平均模型
为了在实际拟合时间序列时有更大的灵活性，有时会将自回归项和移动平均项一起纳入模型，这就引出了自回归移动平均模型（ARMA）：
际中，为了描述一个实际发生的平稳时间序列，往往能够得到自回归、移动平均，或者二者混合的模型，其中p和q的值不大于2，或者常常是小于2的。
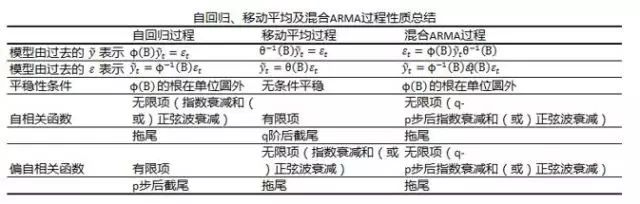
表17.1是针对自回归、移动平均及混合ARMA过程性质的总结。
表17.1 自回归、移动平均及混合ARMA过程性质总结
5. 非平稳模型
在工商业中，常会遇到许多序列（如股票价格）都表现出了非平稳的特性，比如说不围绕一个固定的均值变化。然而这样的序列可能会表现出某种相同的特征，具体来说，虽然这些波动的总体水平在不同时间里其表现是不同的，但是在允许水平有差异的前提下，这些序列的其他广义特征可能是相似的。有些情况下，某种序列在经过一阶或者多阶向后差分后可以转换为平稳时间序列。
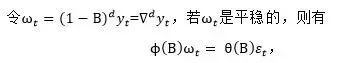
也就是说，描述具有该种同质非平稳特征的模型可以表示为
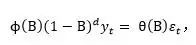
在实际应用中，d通常是0或1，或者最多是2。当d=0时与平稳特征相一致。
对于高阶d也可以定义同样的计算。因此，一般的自回归求和移动平均过程（ARIMA）就是对平稳过程作d次求和而生成的。后面将描述如何使用上述模型的一个具体形式来表达非平稳时间序列。
SAS时间序列分析软件简介
在SAS系统中，有四大模块可以用来进行时间序列分析：
BASE SAS：利用第一篇中介绍的基本编程语言和时间序列的理论知识进行建模和预测。
SAS/STAT：运用最小二乘法对历史数据或者残差进行回归。
SAS/ETS：是SAS系统中专门进行时间序列预测的模块，提供了多种PROC步，对带有时间标识的序列进行处理、建模和预测。本章主要介绍运用该模块中的PROC步进行建模。
SAS Forecast Server：是一种具有可扩展性的大型自动化预测解决方案，具有友好的图形用户界面（如图17.6所示），在较少人工干预的情况下，可快速自动生成大量高质量的统计模型，能自动选择最合适的统计模型，并生成预测。
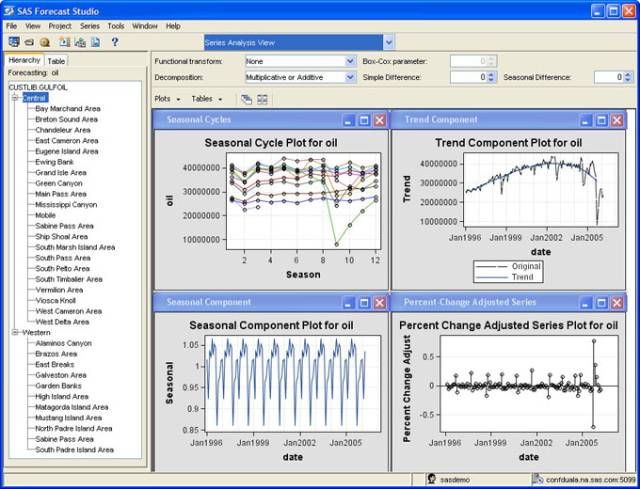
图17.6 SAS Forecast Server的用户界面
平稳时间序列是时间序列中一类重要的时间序列，对于该时间序列，有一套非常成熟的平稳序列建模方法，这也是本节中将重点介绍的部分。
平稳时间序列分析介绍
平稳时间序列是时间序列中一类重要的时间序列，对于该时间序列，有一套非常成熟的平稳序列建模方法，这也是本节中将重点介绍的部分。对于非平稳序列，可以通过差分、提取确定性成分等方法，将转化成平稳序列，再运用平稳序列建模方法进行建模。
在实际操作中，由于样本数据的匮乏，要根据样本数据要找到生成样本的真实随机过程基本是不太可能的。理论研究表明，任意平稳时间序列都可以由ARMA过程（包括AR过程、MA过程和混合过程）近似表示，并且通过ARMA模型可以对序列作出比较精确的预测。
Box-Jenkins建模方法是关于如何分析平稳时间序列、建立ARMA模型以及进行预测的方法，它也是目前比较流行的一种建模方法，建模过程基本可以分为三步，如下：
模型识别：考察时间序列特征，进行模型识别，辨识出有价值且参数简约的模型子类，如AR（3）、ARMA（2,2）等。
参数估计和诊断检验：对已辨识出的模型子类进行数据拟合和参数估计，在恰当的条件下，有效地运用样本数据对模型参数进行推断和估计，并对模型进行诊断检验，通过检验拟合模型与数据的关系来揭示模型的不当之处，从而对模型进行改进。模型识别、参数估计和诊断检验是不断循环和改进的过程，通过该过程来找到合适的模型表达式。
预测：利用拟合好的时间序列模型来推断序列其他的统计性质或预测序列将来的发展。
通常要求，用来建模的观测值的个数至少有50个，最好是100个或更多。当无法获得50个或者更多的历史观测时，例如进行某种新产品的需求预测时，可以使用经验或者类似产品的历史需求信息得到一个初始模型；当获得更多的数据时，这个模型可以随时被更新。
在进行建模时，应使用包含尽可能少的参数的模型，以获得数学上的充分表达。这就是参数使用的简约性原则，该原则在实际应用中是非常重要的。如果模型不恰当，私募工场ID：Funds-Works，老板娘微信guo5_guoguo，或参数使用冗余，将会使预测出现严重问题。因此，在模型选择时，谨慎和反复试探是非常必要的，这也是一个不断改进、修正错误和试验的过程。
广义的Box-Jenkins建模方法也可以建立带趋势和季节因素的时间序列，并且可以根据需要在模型中添加其他输入变量。
数据准备
在实际应用中，我们得到的数据往往是一些交易数据，没有固定的时间间隔，这些数据很多情况下不能直接用来进行时间序列分析，需要先对数据进行预处理，例如将交易数据转化成固定间隔的时间序列，进行数据转换，补全缺失数据，检查是否有异常值等。
数据的预处理是时间序列分析的重要组成部分，会直接影响预测的准确度。因此，在进行股票每天交易量预测的时候，首先需要将股票交易数据转化成按天交易的数据；在对汽车的月度需求进行预测时，需要将汽车按天的销售量累积到按月计算的销售量，等等，这些处理都是为了保证预测足够准确。
TIMESERIES过程和EXPAND过程主要用来整理时间序列数据资料，比如说将短时间间隔数据（每天的交易数量）汇总成长时间间隔数据（月度交易数量），或者将长时间间隔数据（季度销售总量）拆分成短时间间隔数据（月度销售总量），或者自定义时间间隔生成新的时间序列。
运用TIMESERIES过程将短时间间隔数据转换成长时间间隔数据的基本语法如下：
其中：
ID语句指定时间变量，时间变量是指包含时间数据的变量。在使用TIMESERIES过程之前，数据集必须按照分类变量和时间变量排序。
选项INTERVAL=指定输出数据集的时间间隔，取值可以为DAY、WEEK、MONTH、QUARTER、YEAR等SAS日期间隔取值或者SAS时间间隔取值。
选项ACCUMULATE=指定了累积方法，取值有TOTAL、AVERAGE、MEDIAN、FIRST、LAST等。
选项SETMISSING=指定缺失值处理方法，取值有MISSING、0、AVERAGE、MEDIAN、FIRST、LAST等，SETMISSING=的默认值是MISSING。
选项START=和选项END=指定时间变量的起始时间和终止时间，过程步只处理和输出落在这一时间段的观测。
通过TIMESERIES过程得到的输出数据集，是固定时间间隔的序列，可以被用来进行时间序列分析和建模。
例17.1： 数据集ex.stockdaily中包含了某上市公司从1995年9月到2011年7月之间每天股票的价格和交易量信息，具体如下：
Date: 交易日期
Open：开盘价
High：最高价
Low：最低价
Close：收盘价
Volume：交易量
LogVolome：交易量的Log形式， LogVolume=Log（Volume）
Year：交易年份
Month：交易月份
部分数据如图17.7所示。
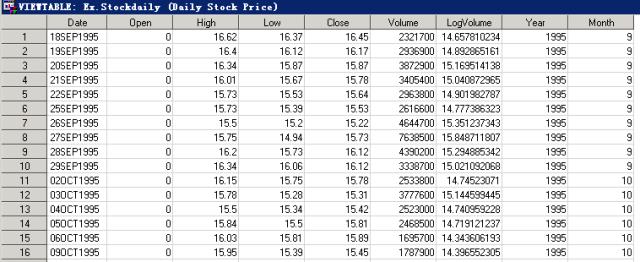
图17.7 数据集ex.stockdaily部分内容
该数据是按天统计的股票信息数据，现在要用TIMESERIES过程，将1995年10月1日到2011年2月28日之间按天统计的数据转换成月度数据。代码如下：
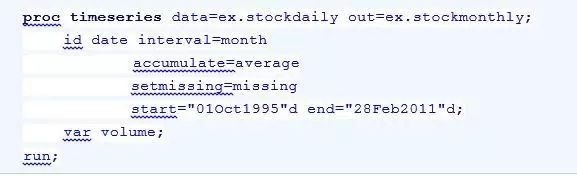
在上述程序中，需要汇总的变量是volume，INTERVAL=MONTH指定输出数据集中数据的时间间隔为月，每天交易量的平均值将作为汇总后的数据存储在变量volume中；在原始数据集ex.stockdaily中，如果在1995年10月1日到2011年2月28日间，缺少某个月份的数据，那么在输出数据集中，将自动生成一条该月份的数据，并且volume的取值为缺失（取值由选项SETMISSING=MISSING指定）。
转换后的数据如图17.8所示。
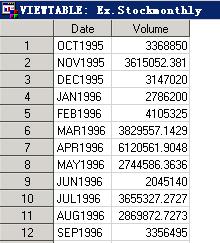
图17.8 数据集ex.stockmonthly部分内容
在数据准备的过程中，另一个重要的过程步是EXPAND过程。EXPAND过程用来把时间序列从一种采样间隔或频率转换为另外一种，并且补插这一时间序列中的缺失值。使用EXPAND过程可以把高频率间隔的时间序列数据转换为较低频率间隔，反之亦然。私募工场ID：Funds-Works，老板娘微信guo5_guoguo，例如，可以把以季度为频率间隔的时间序列处理（譬如汇总、取均值或期末值等）为以年度为频率间隔的时间序列，也可以在一个以年度为频率间隔的序列中补插季度估计，得到以季度为频率间隔的时间序列。EXPAND过程的基本语法为：
其中：
和TIMESERIES过程一样，在使用EXPAND过程时，输入数据集必须已经按照分类变量和时间变量排过序。
在PROC EXPAND语句中，选项FROM=指定输入数据集时间间隔，选项TO=指定输出数据集时间间隔，默认情况下，选项TO=的取值为输入数据集的时间间隔。当选项FROM=DAY，TO=DAY时，如果输入数据集中，缺少某一天的数据，那么在输出数据集中，将自动生成一条新的数据，并且在日志中，会生成一条警告信息。
选项METHOD=可以指定插值方法，取值有SPLINE、JOIN、STEP、AGGREGATE和NONE，当取值为NONE时，表示不进行插值。PROC EXPAND语句和CONVERT语句中都可以使用选项METHOD，但是CONVERT语句中选项METHOD的优先级更高。
例17.2： ex.stockdaily数据集中的股票数据是按天收集的，但是因为一些原因，使得该数据集中并没有包含所有交易日的数据，也就是说，某些交易日的数据被遗漏掉了。要使得分析的序列是固定时间间隔的，可以运用EXPAND过程对该序列进行预处理。
示例代码如下：
部分日志信息如图17.9所示。
图17.9 例17.2日志中警告信息
该日志显示在输入数据集中，1995年11月22日和11月24日之间缺少一条数据，在输出数据集中，将自动生成一条新的观测，Date的取值为1995年11月23日。由于选项METHOD=NONE，因此，新观测的Volume和Logvolume的取值为缺失（如图17.10所示）。
图17.10 例17.2日志信息
原始数据集ex.stockdaily中包含4000条数据，经过EXPAND过程处理后，增加了部分数据，变为了4130条数据。
EXPAND过程的用法非常灵活，还可以将某种固定间隔的时间序列转换成其他任意指定时间间隔的数据（查看SAS帮助文档中选项FACTOR的用法），并且可通过指定的方法补插时间序列中的缺失值。
平稳性和白噪声检验
1. 平稳性的图检验
拿到一个时间序列之后，首先是判断它的平稳性。判断一个序列是否平稳有两种检验方法，一种是图检验方法，即根据时序图和自相关系数图显示的特征做出判断，一种是单位根检验法，即构造检验统计量进行假设检验的方法。
图检验方法是一种操作简便、运用广泛的平稳性判别方法，但是判别结论容易带有一定的主观性，所以最好能辅以统计检验方法进行判断。
根据平稳时间序列均值和方差为常数的性质可知，平稳时间序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的范围有明显的相似性特点。如果时序图显示出该序列有明显的趋势性或者周期性，那么它通常不是平稳序列。根据这个性质，很多非平稳序列通过查看时序图就可以被识别出来。
我们知道，自相关函数是用来描述时间序列中不同观测之间的线性相关程度的，可以证明平稳时间序列通常都具有短期相关性，具体描述就是随着延迟期数k的增加，平稳序列的自相关系数
会很快衰减向零。反之，非平稳序列的自相关系数衰减向零的速度通常比较慢。这就是我们利用自相关图进行平稳性判断的标准。自相关图，也称ACF图，全称为Autocorrelation Function Plot，横坐标表示延迟期数（也称滞后期数），纵坐标表示自相关系数的取值，图中每一个柱子都代表了某延迟期数对应的自相关系数的取值。观察以下两组序列的时序图和ACF图（如图17.11和图17.12所示），可以明显看出，图17.11中的序列随着时间的变化有明显的上升趋势，是非平稳的，因此自相关系数衰减的速度很慢，而图17.12中平稳序列的自相关系数则衰减很快。
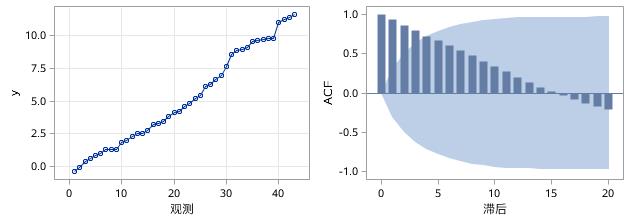
图17.11 非平稳时间序列序列图和ACF图
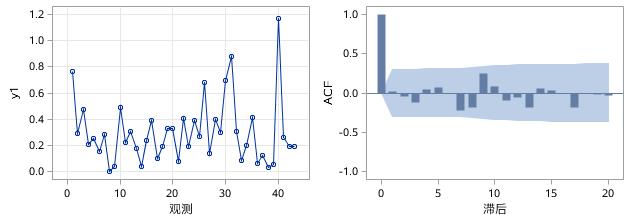
图17.12平稳时间序列序列图和ACF图
另一种常见的平稳性检验方法是单位根检验（Unit Root Test），在后面介绍趋势时间序列时将重点讲解。
2. 白噪声检验
并不是所有的平稳序列都值得建立模型，只有那些序列值之间具有相互依赖性，历史数据对未来的发展有一定影响的序列，才值得建模，建模是为了预测序列未来的发展。如果序列值彼此之间没有任何相关性，譬如白噪声序列，过去的行为对将来的发展没有丝毫影响，从统计分析的角度而言，是没有任何分析建模的价值的。
为了判断某个序列是否值得继续分析建模，需要对其进行白噪声检验。由白噪声序列的定义知，对于任意k期延迟，都有自相关系数=0，k>0。需要指出的是，这是理想的状况，实际上，由于样本序列的有限性，会导致白噪声序列的样本自相关系数不会绝对为零。
随机产生一个服从标准正态分布的白噪声序列，然后观察它的时序图和自相关系数图，如图17.13和图17.14所示。
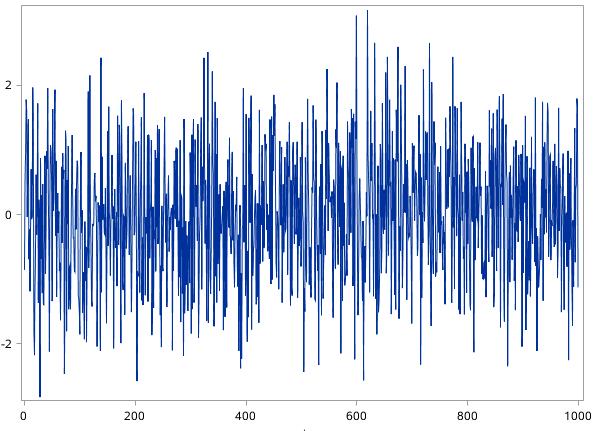
图17.13 随机产生的服从标准正态分布的白噪声序列的时序图
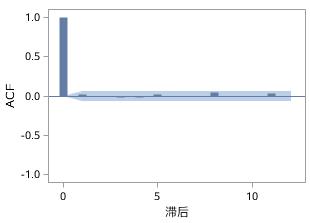
图17.14 白噪声序列的自相关系数图
在图17.14中可以看到，这个白噪声序列的大部分样本自相关系数都不等于零，但是这些自相关系数都非常小，都在零值附近以一个很小的幅度做着随机波动。
Barlett证明，如果一个时间序列是白噪声序列，样本长度为n，那么该序列的非0期延迟期数的样本自相关系数将近似服从均值为零、方差为样本长度倒数的正态分布，即
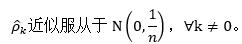
既然样本自相关系数的分布具有这样的性质，那么就可以构造统计量从统计意义上来检验时间序列是否为白噪声序列了。
这里，我们不去单独地考虑每一个，而是将前m个自相关系数作为一个整体来考虑，通过它们构造一项指标来判断序列是否是白噪声序列。由于序列取值之间的变异性是必然的，而相关性是偶然的，因此一定要有足够的证据才能证明序列之间存在相关性。若进行白噪声检验的原假设和备择假设分别为：
如果序列是白噪声序列，根据正态分布和卡方分布的关系，可以证明LB统计量近似服从自由度为m的卡方分布；反之，如果序列不是白噪声序列，则LB的取值会陡增。若给定显著性水平a，可以计算出卡方分布在1-a处的分位数
，如果由样本序列计算出来的LB统计量大于，则说明有充足的理由拒绝原假设，也就是说使得，即该时间序列不是白噪声序列。
白噪声检验不仅可以用在对原始时间序列的检验中，也可以用在对残差序列的检验中。如果模型已经从序列中提取出了所有的有用信息，那么残差序列应该就是一个白噪声序列，否则的话，说明序列中某种规律性的信息没有被模型表示出来，也就是说，模型是拟合不足的。
（1）ARIMA过程
SAS中的ARIMA过程是根据Box-Jenkins建模方法开发的一个过程步，专门用来建立ARIMA模型（包含AR模型、MA模型、混合ARMA模型和ARIMA模型等），基本语法如下：
其中：
IDENTIFY语句：用来指定需要分析的时间序列，并计算和输出多种统计量及相关关系图供用户进行序列分析，识别合适的模型。
ESTIMATE语句：用来建立模型，为前面IDENTIFY语句中指定的响应变量拟合ARMA模型或转移函数模型，计算其参数的估计值；并输出诊断信息，从而判断模型是否不足。
OUTLIER语句：用来检测ESTIMATE语句中建立的模型没有能够处理的异常值，在使用该语句前，必须先使用ESTIMATE语句。
FORECAST语句：根据ESTIMATE语句中计算的参数估计，生成时间序列的预测值。
ARIMA过程实现步骤和前面介绍的Box-Jenkins建模方法的步骤非常类似，同样是由模型识别、估计、诊断到预测。在ARIMA过程中有诸多的选项可实现不同的分析要求，接下来结合例子进行介绍。
例17.3：在例17.2中，已经运用EXPAND过程将原序列转换成了等间隔的时间序列，接下来，运用ARIMA过程考察ex.stockdaily中的股票交易量序列（仅考察从2010年1月1日开始的数据），并对序列进行平稳性检验和白噪声检验。
示例代码如下：
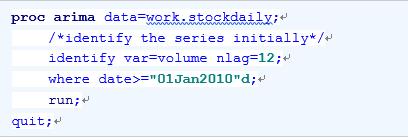
在上述代码中，IDENTIFY语句使用了选项NLAG=，该选项指定一个数字告诉系统在计算样本自相关函数、样本偏自相关函数和样本逆自相关函数时所需考虑的最大延迟期数。为获得一个ARIMA(p, d, q)模型的初步估计，NLAG=的取值最小必须为p+d+q。数据集中观测的个数必须大于等于NLAG=的取值。NLAG=的默认值为24和观测个数的四分之一这两个数字中较小的一个。
图17.15中展示的表是ARIMA过程输出的第一部分：序列的基本统计量和白噪声检验结果。
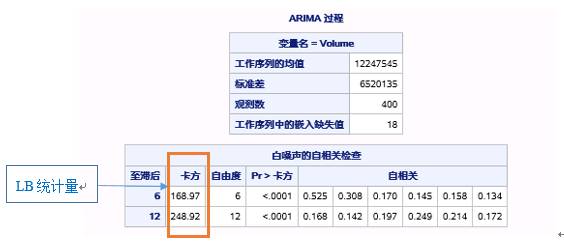
图17.15 例17.3序列基本信息和白噪声检验
由于程序中指定了NLAG=12，故白噪声检验的最大延迟期数也为12。白噪声的自相关检查报表输出了m=6和m=12的检验结果（回归“白噪声检验”中的m的取值），需要指出的一点是，m的取值为6的倍数。
思考一下，本例中，在进行白噪声的自相关性检验时，只检验了至多延迟12期的LB统计量是否合适？是否需要进行全部400期的延迟检验（从2010年1月1日开始总共有400个观测点）？
事实上，因为平稳序列通常具有短期相关性，如果观测值之间存在显著的相关关系，通常只存在于延迟期数比较短的观测值之间。所以，如果一个平稳序列短期延迟的观测值之间都不存在显著的相关关系，通常长期延迟之间就更不会存在显著的相关关系了。另一方面，如果一个平稳序列显示出显著的短期相关性，那么该序列就一定不是白噪声序列。因此，这里只检验至多延迟12期的LB统计量已经足够。
ARIMA过程的第二部分输出为时序图、样本自相关系数图（ACF）、样本偏自相关系数图（PACF）和样本逆自相关系数图（IACF）（如图17.16所示）。PACF图和IACF图是相应的以延迟期数为横坐标、样本偏自相关系数和样本逆自相关系数为纵坐标的柱状图。
ACF图、PACF图和IACF图在模型识别和参数估计中具有重要作用，这在下一节中将详细介绍。
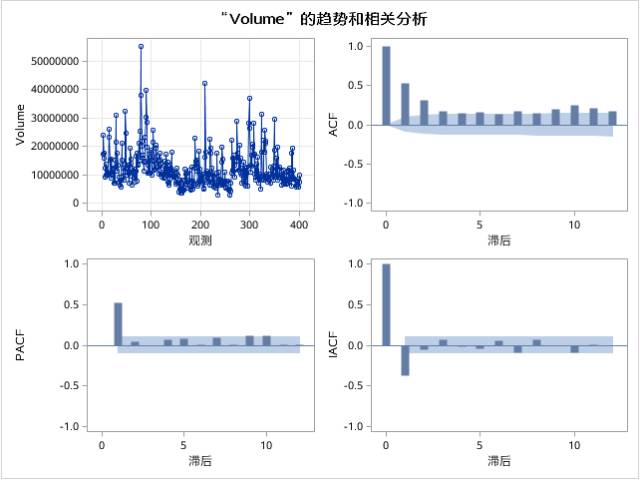
图17.16 例17.3中序列的趋势和相关分析
根据时序图和ACF图，即可进行大致的平稳性检验，从时序图中，基本可以判断观测值通常是以固定的波动幅度围绕在一个固定水平波动的；根据ACF图的判断准则，样本自相关系数在2阶延迟之后很快衰减向0（虽然在10阶延迟附近出现振荡），基本可以判断该序列是一个平稳时间序列。
综合前面的白噪声检验结果，说明该序列不仅可以视为平稳序列，而且还蕴含着值得提取的相关信息。
运用自相关函数和偏自相关函数的性质识别
先来回忆一下在前面章节中曾讨论过的内容：有关移动平均、自回归和混合过程的理论，以及自相关和偏自相关函数的特征行为。
简要地说：
p阶自回归过程的自相关函数是拖尾的，而它的偏自相关函数在p阶延迟之后是截尾的。
q阶移动平均过程的自相关函数在延迟q阶之后是截尾的，而它的偏自相关函数是拖尾的。
若自相关函数和偏自相关函数均拖尾，则表明是混合过程。进一步，对于一个包含p阶自回归和q阶移动平均的混合过程来说，其自相关函数在q-p阶延迟之后是混合的指数和正弦波衰减。与此相应的，混合过程的偏自相关函数在q-p阶延迟之后被混合的指数和正弦波衰减所控制。
但在实践中，依据这些性质为模型定阶是有一定困难的。因为由于样本的随机性，样本的相关系数不会呈现出理论上的完美截尾情况，比如，本应截尾的样本自相关系数或偏自相关系数仍然会呈现出小值振荡的情况。这种现象导致我们必须判断，什么情况下该看作相关系数是截尾的，什么情况下该看作相关系数是在延迟若干阶之后正常衰减到零值附近做拖尾波动的呢？
对于较大的延迟，假设在q阶移动平均过程下，我们用样本估计值代替理论自相关系数，可以根据Bartlett公式计算出样本自相关系数的标准差：
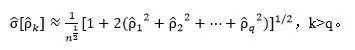
对于偏自相关函数，和前面讨论的一样，在过程为p阶自回归的假设中，p+1阶或更高阶偏自相关系数的估计值的标准差是
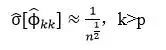
对于适当大小的n，假设理论自相关系数
为零，它的估计值
服从近似正态分布，对于偏自相关系数有类似的结论。
这些事实可以提供一种非正式的标准，用来指示当延迟超出某特定值后理论自相关函数和偏自相关函数是否实质上为零。
根据正态分布的性质：
如果样本自相关系数或偏自相关系数在最初的k阶的取值明显大于2倍标准差范围，而在k阶之后几乎95%的样本相关系数都落在2倍标准差的范围以内，形成了小值波动；而且样本自相关系数由较大值衰减到2倍标准差范围内的过程非常突然，这时，通常视为相关系数截尾，阶数为k。
如果样本自相关系数或偏自相关系数在最初的k阶的取值明显大于2倍标准差范围，而k阶之后有超出5%的样本相关系数落入2倍标准差范围之外；或者是由显著非零的相关系数衰减为小值波动的过程比较缓慢或者非常连续，这时，通常视为相关系数不截尾。
注意：由于自相关函数的估计之间可能高度相关，因此，不可能指望自相关函数的估计值与理论值十分贴近。特别是，当理论自相关函数已经衰减了，而自相关函数的估计还可能出现相当大的、明显的波动和趋势，这种相悖的现象在理论中是没有依据的。在运用自相关函数的估计作为识别依据时，通常能对大致的特征有相当的把握，至于那些更精细的特征，它们可能未必代表真实的结果，因此，可能需要引入两个或更多的模型，以便在建模的估计和检验诊断阶段作进一步的研究。
除了样本自相关系数和样本偏自相关系数之外，样本逆自相关系数也可以用来帮助模型定阶。样本逆自相关系数和样本偏自相关系数的估计值符号相反，当样本偏自相关系数的截尾或者拖尾性质难以判断时，可以参考样本逆自相关系数的截尾或者拖尾性质来作出判断。
一阶、二阶AR过程和MA过程以及简单的混合ARMA过程都是特别重要的，接下来通过例子具体查看这类过程的相关系数的特征。
例17.4：通过例子分析一阶、二阶AR过程和MA过程以及混合ARMA过程的时序图、ACF图、PACF图和IACF图特征。
示例代码如下：
上述程序生成了8个时间序列Y1，Y2，…，Y8。Y1是AR（1）过程生成的时间序列；Y2和Y3分别是由不同的AR（2）过程生成的时间序列；Y4是MA（1）过程生成的时间序列；Y5和Y6分别是由不同的MA（2）过程生成的时间序列；Y7是ARMA（1,1）过程生成的时间序列；Y8是白噪声序列。接下来运用ARIMA过程输出各个时间序列的时序图、ACF图、PACF图和IACF图。代码如下：
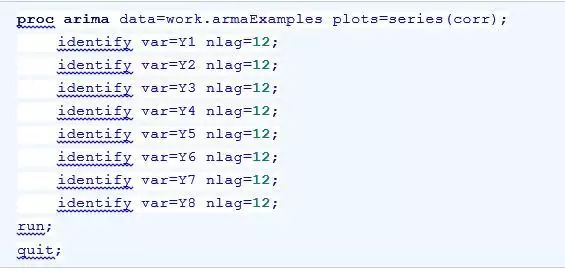
输出内容如图17.17至图17.24所示（其中省略了序列的基本信息和白噪声检验结果）。
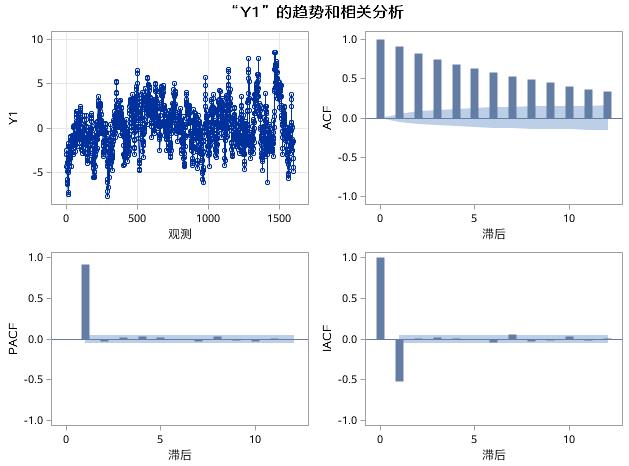
图17.17 例17.4中序列Y1的趋势和相关分析
在图17.17中，Y1是AR（1）过程生成的时间序列，样本自相关系数是指数衰减的，
，从生成Y1的代码中可以看出
=0.9。在PACF和IACF图中，1阶延迟后，偏自相关系数和逆自相关系数都迅速衰减为小值波动，且落在了2倍标准差范围内，符合截尾特征。
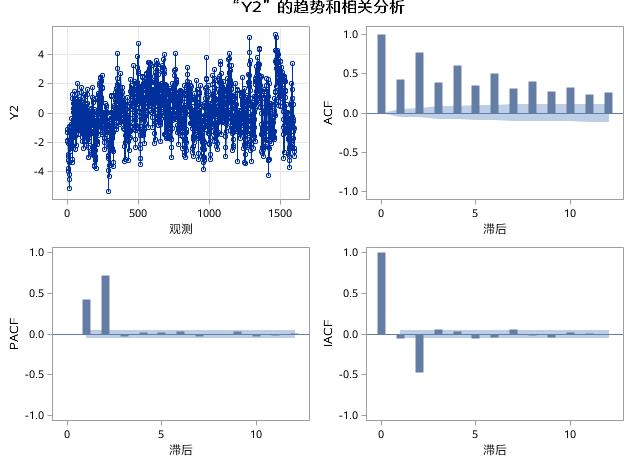
图17.18 例17.4中序列Y2的趋势和相关分析
如图17.18所示，在Y2的ACF图中，自相关系数呈现出类似指数衰减的特征，在PACF和IACF图中，2阶延迟后，偏自相关系数和逆自相关系数都迅速衰减成小值波动，具有截尾特征，符合AR（2）过程的相关系数的特征。
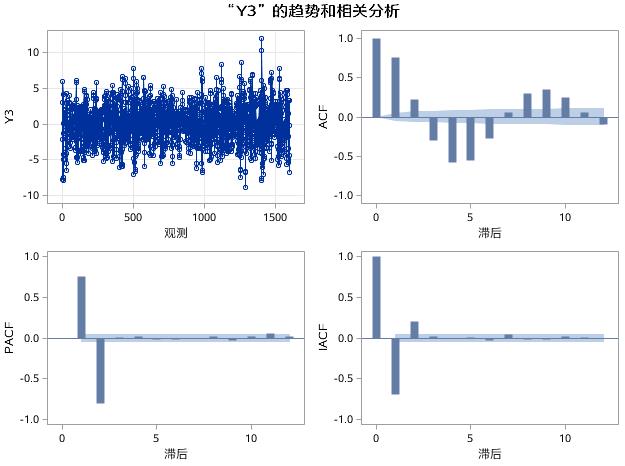
图17.19 例17.4中序列Y3的趋势和相关分析
如图17.19所示，Y3的PACF图和IACF图的形状和特征与Y2的非常类似，也都是延迟2阶之后截尾；不同的是，在Y3的ACF图中，自相关函数呈现出正弦波振荡衰减的特征，符合AR（2）的相关系数特征。
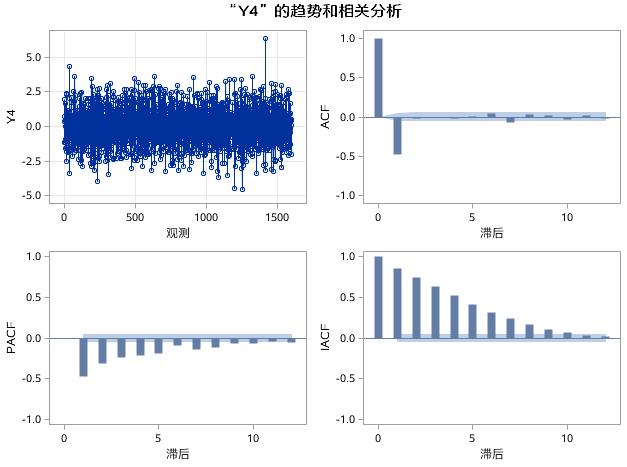
图17.20 例17.4中序列Y4的趋势和相关分析
在图17.20中，Y4是MA（1）过程生成的时间序列，ACF图呈现出明显的截尾特征，在1阶延迟之后，自相关函数迅速衰减成小值波动，在PACF和IACF图中，偏自相关函数和逆自相关函数都呈指数衰减，具有拖尾的特征。
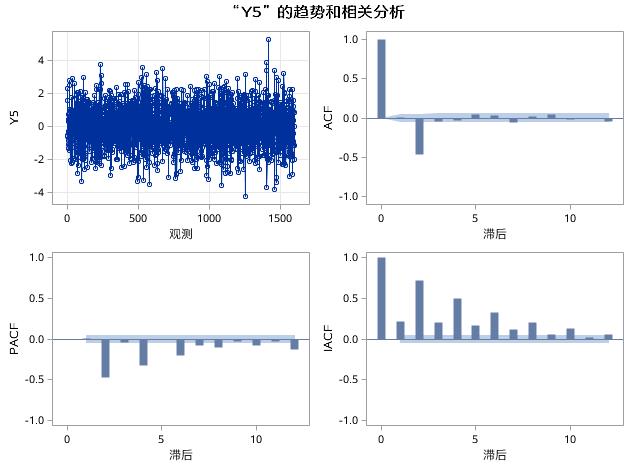
图17.21 例17.4中序列Y5的趋势和相关分析
在图17.21中，Y5是MA（2）过程生成的时间序列，ACF图中，自相关函数在2阶延迟之后，迅速衰减到小值波动，具有截尾特征；PACF图和IACF图都具有明显的拖尾特征。
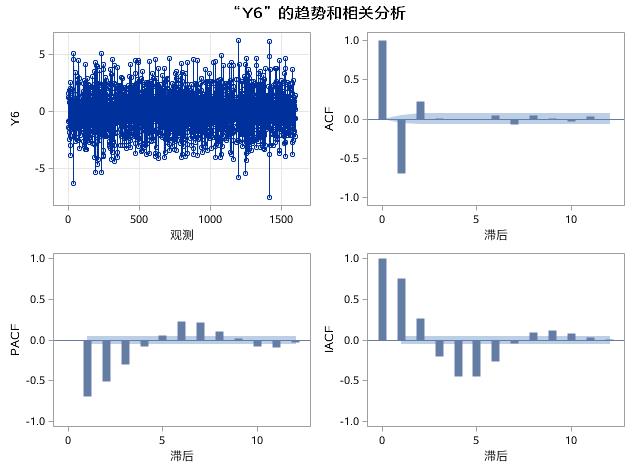
图17.22 例17.4中序列Y6的趋势和相关分析
在图17.22中，Y6是另一种MA（2）过程生成的时间序列，ACF图中，自相关函数在2阶延迟之后，迅速衰减成小值波动，具有截尾特征；PACF和IACF图中，偏自相关函数和逆自相关函数呈现正弦波振荡衰减的特征。
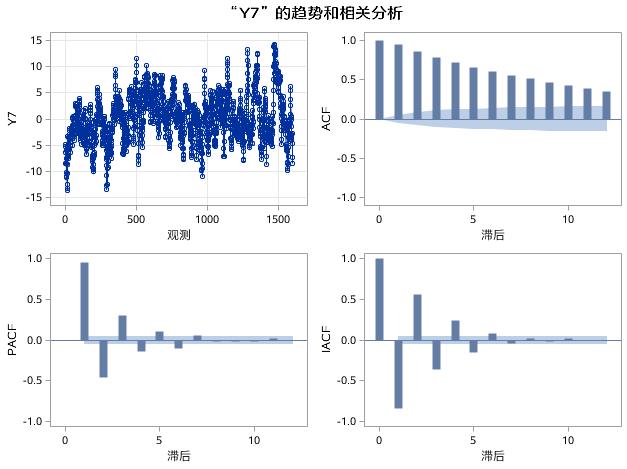
图17.23 例17.4中序列Y7的趋势和相关分析
在图17.23中，Y7的ACF图、PACF图和IACF图都呈现出拖尾的特征，符合混合模型的相关系数特征，但是仅通过相关系数很难判断混合模型的阶数。
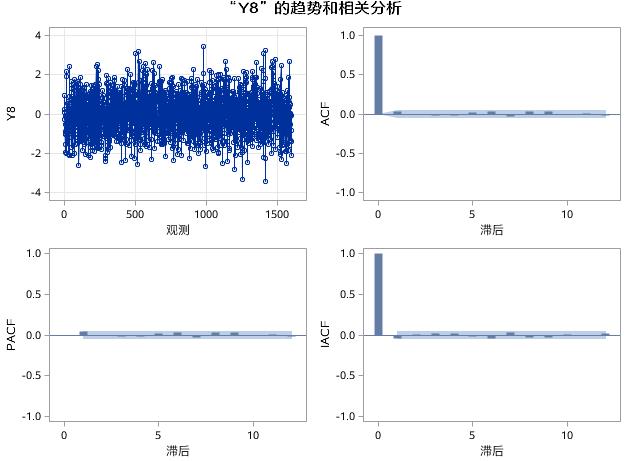
图17.24 例17.4中序列Y8的趋势和相关分析
在图17.24中，Y8是白噪声序列，任意阶延迟的自相关函数、偏自相关函数和逆自相关函数都近似为0。
前面讨论了如何用TIMESERIES过程进行数据的预处理，实际上除了对数据进行预处理以外，TIMESERIES过程也可以用来生成序列的ACF图、PACF图和IACF图，语法如下：
TIMESERIES过程默认不输出任何图形或报表，因此在PROC TIMESERIES语句中，需要使用选项PRINT=和PLOT=来输出指定的报表或图形。当同时指定多个图形或报表时，需要将它们用括号括起来。可以输出的图形包括SERIES、RESIDULE、HISTOGRAM、CORR、ACF、PACF、IACF、WN（白噪声概率）、TCC（trend-cycle component）、SC（seasonal component）等；可以输出的报表包括DECOMP、SEASONS、DESCSTATS、SUMMARY、TRENDS等。
例17.5：利用TIMESERIES过程作出数据集work.armaExamples中序列Y1的相关系数图。
示例代码如下：
输出内容如图17.25和图17.26所示（省略了数据集的基本信息输出和序列的基本信息输出）。
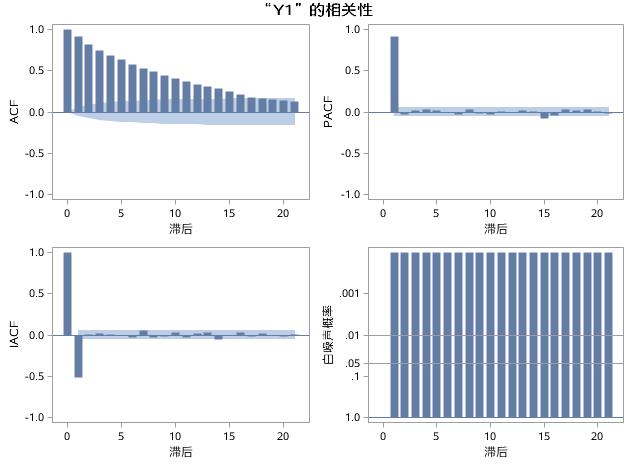
图17.25 例17.5中序列Y1的相关性分析
从图17.25可见，在相关性分析面板里同时输出了Y1的ACF图、PACF图和IACF图，以及白噪声检验图。前三者和ARIMA过程输出的结果一样，这里不再解释。
白噪声检验图以延迟期数为横坐标，以Pr>|延迟期数对应的统计量LB的取值|的概率为纵坐标，每个柱子代表每个延迟期数对应的概率，概率越小柱子越高，图中，任意延迟期数对应的概率都小于0.001，代表着应拒绝白噪声检验的原假设，即Y1不是白噪声序列。
接下来，TIMESERIES过程还将分别输出Y1的ACF图及标准化ACF图、PACF图及标准化PACF图、IACF图及标准化IACF图。下面仅展示ACF图和标准化ACF图作为示例。标准化的ACF图仍然以延迟期数作为横坐标，以标准化之后的ACF作为纵坐标，它标出了2倍标准差范围和1倍标准差范围。
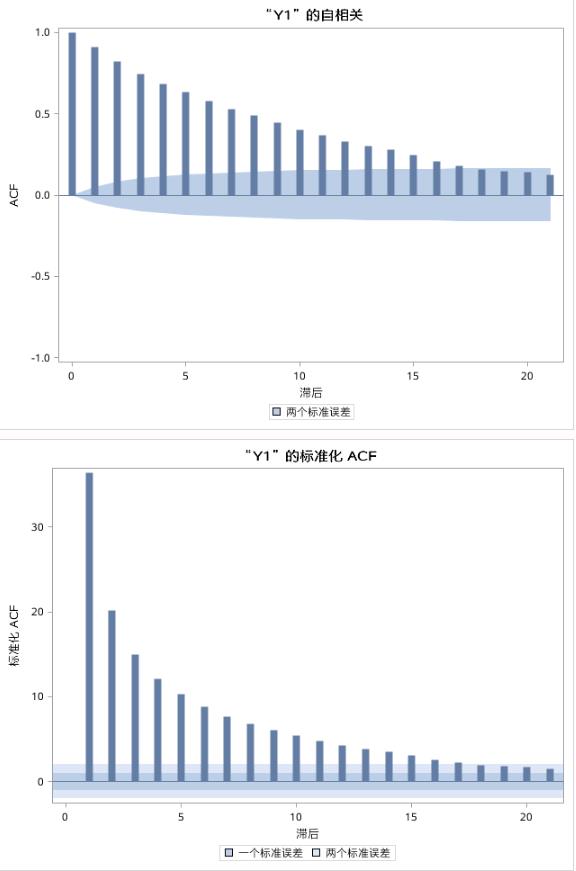
图17.26 例17.5中序列Y1的自相关图和标准化自相关图
自动识别
对于某些序列，通过观察自相关函数、偏自相关函数和逆自相关函数图，可以判断出AR模型或MA模型的阶数。但是，有的时候，ARMA混合模型可能可以生成更加准确的预测，并且一个合适的ARMA（p，q）模型所含参数的个数（p+q+2）通常要小于纯粹的AR（p'）或者MA（q'）所含参数的个数。但是，从例17.4中的时间序列Y7可知，ARMA混合模型的阶数通过观察相关系数图是很难判断的。
为了更有效和更简便地辨识ARMA模型的阶数，一些其他的模式辨识方法被提出并应用，例如ESACF（延伸自相关系数法）、SCAN（最小典型相关法）和MINIC 方法（最小信息准则法）。在ARIMA过程中，IDENTIFY语句中的选项ESACF、MINIC和SCAN就是分别对应的这三种模式辨识方法的。其使用语法为：
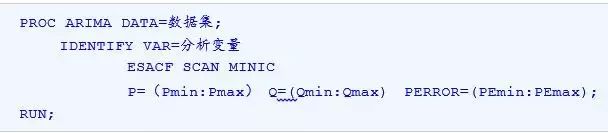
其中，选项P=指定了AR阶数范围，选项Q=指定了MA阶数范围；选项PERROR=指定了用来拟合残差序列的AR模型的阶数范围，默认情况下，PEmin设定为Pmax，PEmax设定为Pmax和Qmax之和。选项ESACF、SCAN和MINIC可以分开使用。
例17.6： 分别用选项ESACF、MINIC、SCAN为work.armaExamples中的序列Y7进行模型识别。
示例代码如下：
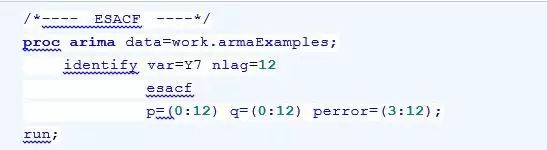
输出的报表中包含了ESCAF方法的广义自相关系数矩阵和P值矩阵，根据这两个矩阵的结果，SAS接着输出了ESACF方法识别出的待选模型，如图17.27所示，待选模型包括ARMA（1,1），ARMA（9，8）和ARMA（10，8）。
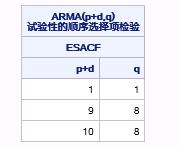
图17.27 例17.6中ESACF方法识别出的待选模型
这里需要解释一下p+d的意思，例如，当p+d=2时，p和d的取值有三种情况：
p=2，d=0
p=1，d=1
p=0，d=2
在前面介绍自回归求和移动平均过程（ARIMA）时曾讲到，如果序列是非平稳的，可先通过差分将非平稳序列转化成平稳序列，d则表示差分的阶数。当d>0时，ARMA模型表示非平稳模型，所以上面ESACF方法也提供了一些待选的非平稳模型。
这里SAS直接输出了根据广义自相关系数矩阵和P值矩阵识别出的待选模型，如果读者感兴趣如何从这些矩阵中分析识别待选模型，可以查看相关参考文献，如Tsay and Tiao (1984)，及Pena，Tiao，and Tsay(2001)。
下面这段程序的输出了SCAN方法的典型相关估计矩阵和卡方统计量的P值矩阵。
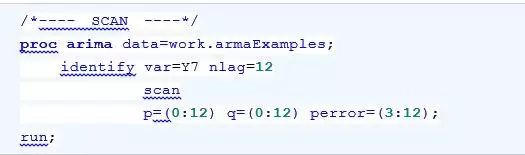
基于对这两个矩阵的分析，SAS接着输出了SCAN方法识别出的模型，如图17.28所示，待选模型包括ARMA（1,1）、AR（8）和一些非平稳模型。注意，ARMA（1,1）同样是ESACF方法推荐的待选模型。
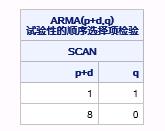
图17.28 例17.6中SCAN方法识别出的待选模型
下面这段程序输出了MINIC方法的信息准则矩阵。
该信息准则矩阵如图17.29所示，并且它基于最小信息准则，给出了推荐的模型ARMA（1,4）。
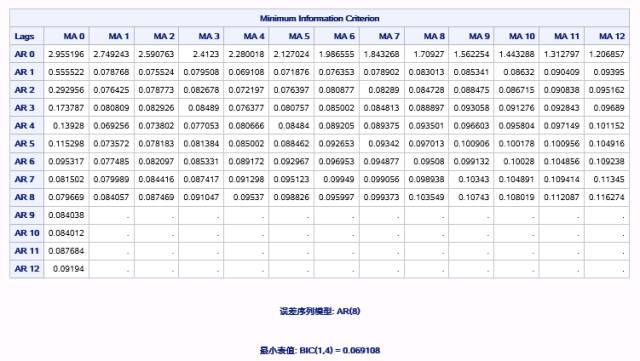
图17.29 例17.6中MINIC方法的信息准则矩阵
那么，通过这三种方法识别的待选模型有ARMA（1,1）、ARMA（9,8）、ARMA（10,8）、AR（8）、ARMA（1,4），并且ESACF方法和SCAN方法都推荐了ARMA（1,1）。
参数估计
前面已经介绍了任何一个平稳模型都可以用ARMA模型来进行逼近，不失一般性，我们把ARMA模型表示成如下形式：
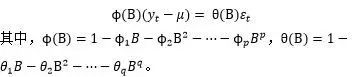
通过上一节的学习，已经知道如何辨识阶数p和q了，接下来，就要根据实际数据来拟合模型中的p+q+2个未知参数
参数是序列均值，通常采用矩估计方法，用样本均值估计总体均值即可得到它的估计值：
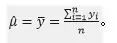
这样一来，原来p+q+2个待估参数就减少为p+q+1个了。对p+q+1个未知参数的估计方法有三种：矩估计、极大似然估计和最小二乘估计。
（1）矩估计
运用p+q个样本自相关系数估计总体自相关系数
在低阶ARMA模型场合下，矩估计方法具有计算量小，估计思想简单直观，且不需要假设总体分布等特点。但是这种估计方法中只用到了p+q个样本自相关系数，样本序列中的其他信息都被忽略了，这导致它的估计精度较差，可见，矩估计方法是一种比较粗糙的估计方法，因此它的值常被用作极大似然估计和最小二乘估计迭代计算的初始值。
（2）极大似然估计
在极大似然的准则下，认为样本来自使得该样本出现概率最大的总体。因此，未知参数的极大似然估计就是使得似然函数
达到最大的参数值，似然函数为：
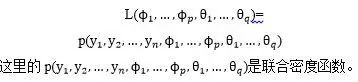
使用极大似然估计必须已知总体的分布函数，而在时间序列分析中，序列总体的分布往往是未知的，为了便于计算和分析，通常假设序列服从多元正态分布。
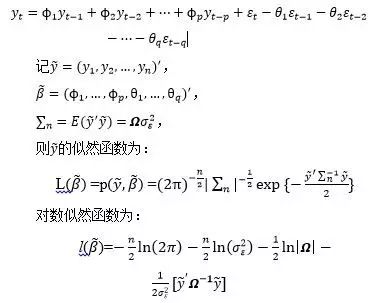
对对数似然函数中的未知参数
求偏导数，就可以得到似然方程组。理论上，求解似然方程组即得到未知参数的极大似然估计值。但是，由于
都不是参数的显式表达式，因而似然方程组实际上是由p+q+1个超越方程构成的，通常需要经过复杂的迭代算法才能求出未知参数的极大似然估计值。
极大似然估计法充分应用了每一个观测值所提供的信息，因而它的估计精度较高，同时还具有估计的一致性、渐进有效性等优良的统计性质。
（3）最小二乘估计
在ARMA（p,q）模型中，记
未知参数的最小二乘估计值通常也得借助迭代法求出，并且由于充分了序列观测值的信息，因而最小二乘估计的精度也很高。
在实际运用中，最常用的是条件最小二乘估计法，它指定过去未观测到的序列值等于样本序列的均值。
虽然极大似然估计的计算量要大于最小二乘估计，但是，研究表明，极大似然估计要优于最小二乘估计，特别是对样本长度比较小的时间序列。
ARIMA过程中，考虑到计算量等因素，默认的参数估计方法是条件最小二乘估计；但是，通过长期的实践，SAS和很多使用SAS进行预测的专家都推荐使用极大似然估计做为参数估计的方法。
使用ARIMA过程进行参数估计的语法为：
其中，ESTIMATE语句是ARIMA过程中进行参数估计的语句，选项P指定了进行自回归的阶数，选项Q指定了移动平均的阶数，选项ML指定了使用极大似然估计作为参数估计的方法，也可以用METHOD=ML来指定使用极大似然估计法，默认METHOD=CLS，表示使用条件最小二乘估计法。
例17.7： 在例17.6中已经识别出了一组待选模型，下面根据参数使用简约性原则，对待选模型ARMA（1,1）进行参数估计。
示例代码如下：
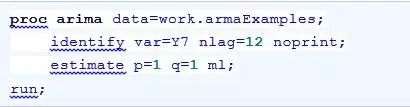
输出内容如图17.30和图17.31所示。
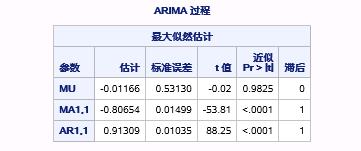
图17.30 例17.7中ARMA（1,1）模型参数估计报表
在图17.30中，显示的是极大似然估计（也称为最大似然估计）的参数估计和显著性报表。在ARMA（1,1）模型中，均值项记为MU，其估计值为-0.01166，对应着“MA1,1”，对应着“AR1,1”，很明显，参数“MA1,1”和“AR1,1”都是显著不为零的。
图17.31 例17.7中ARMA（1,1）模型信息
当有多组待选模型时，可以在同一ARIMA过程中多次使用ESTIMATE语句进行参数估计。
诊断检验
模型诊断检验过程将通过计算多个诊断统计量来衡量模型的拟合优度和准确度，并对模型的残差序列进行相关性检验和正态性检验。
衡量模型拟合优度的准则一般有两个：
AIC准则：即Akaike’s Information Criterion，是衡量统计模型拟合优良性的一种标准，它是由日本统计学家赤池弘次创立和发展的，又称赤池信息量准则，它建立在熵的概念基础之上，可以权衡所估计模型的复杂度和该模型拟合数据的优良性。AIC准则鼓励数据拟合的优良性，但是也表示应尽量避免出现过度拟合(Overfitting)的情况。
SBC准则：即Schwarz’s Bayesian Information Criterion，和AIC准则类似，但在计算公式上面略有差别。
当有多个待选模型时，应优先考虑AIC值或者SBC值小的模型。这两个准则在很多进行模型拟合的过程步中都会用到。
衡量模型准确度的统计量有：
当序列值有可能为零时，推荐使用SMAPE。MAPE在商业预测和分析中应用得比较多。当有多个待选模型时，可以通过计算MAPE和RMSE等统计量来衡量模型的准确性。
在例17.7中，在参数估计报表后面输出了ARMA（1,1）模型的拟合优度报表，如图17.32所示。
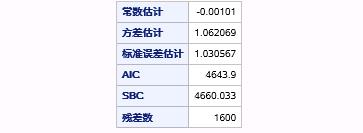
图17.32 例17.7中ARMA（1,1）模型拟合优度报表
接着，又输出了残差序列的诊断检验结果，如图17.33和图17.34所示。残差序列的ACF图、PACF图、IACF图和白噪声序列Y8的对应相关系数图非常类似，并且白噪声概率都大于0.05，表示残差序列值之间不存在依赖关系。残差序列的直方图和Q-Q图也表示残差序列服从正态分布。
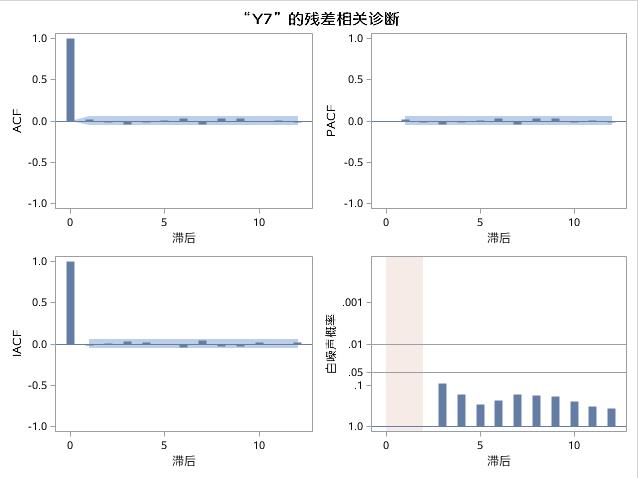
图17.33 例17.7中ARMA（1,1）模型残差诊断
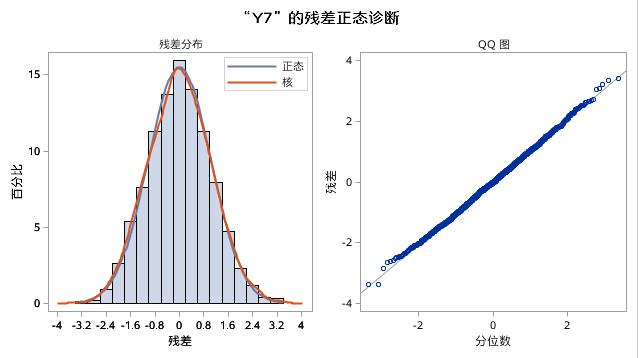
图17.34例17.7中ARMA（1,1）模型残差正态诊断
白噪声检验不仅可以用在对原始时间序列的检验中，也可以用在对残差序列的检验中。如果模型已经从序列中提取出了所有的有用信息，那么残差序列应该是一个白噪声序列，否则，说明序列中某种规律性的信息没有被模型表示出来，也就是说，模型是拟合不足的。
预测语句FORECAST
在参数估计和诊断检验完成后，就可以利用拟合出的模型进行预测了。ARIMA过程进行预测的语句为FORECAST语句，使用方法如下：
其中，FORECAST语句会根据ESTIMATE语句中使用的模型及估计出的参数，生成时间序列的预测值。因此，在ARIMA过程中，使用FORECAST语句前，一定要先使用ESTIMATE语句。选项LEAD指定需要向后预测多少个时间点，选项ID和INTERVAL分别指定时间变量和时间间隔，选项OUT指定输出数据集。
平稳序列分析全过程
接下来，通过一个完整的示例来介绍对一个平稳序列进行分析的全过程。
例17.8：数据集ex.weeklysales中包含了一家汽车零部件店里三种零件从2010年1月开始到2012年10月份每周的销售量，数据集中包含四个变量，具体如下：
OrderDate：每周的第一天，代表一周
Part1：零部件1每周的销量
Part2：零部件2每周的销量
Part3：零部件3每周的销量
现在希望预测这三种零件未来每周的销量。
因为数据已经准备完毕，那么，根据时间序列分析的流程，我们可以跳过第一步，直接来查看序列是否平稳，以及序列中是否包含值得提取的信息，并进行模型识别。示例代码如下：
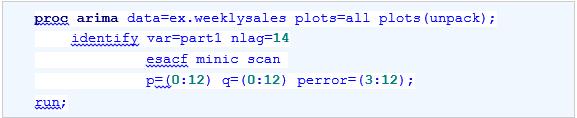
选项UNPACK指定系统输出较大的时序图、ACF图、PACF图和IACF图。
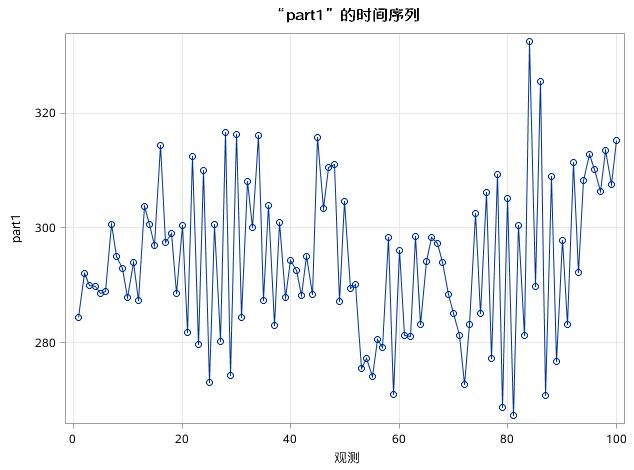
图17.35 例17.8中序列PART1的时序图
从时序图来看（如图17.35所示），part1没有明显的趋势或者季节性因素。
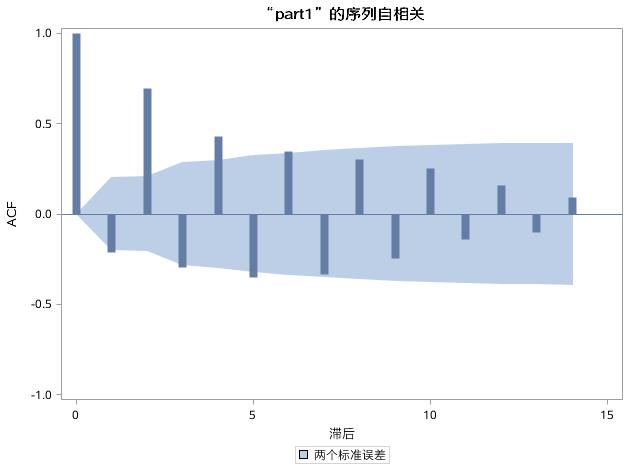
图17.36 例17.8中序列PART1的自相关图
ACF图中，自相关系数在4阶延迟期后即衰弱成小值振荡，与MA（4）的特征相符（如图17.36所示）。
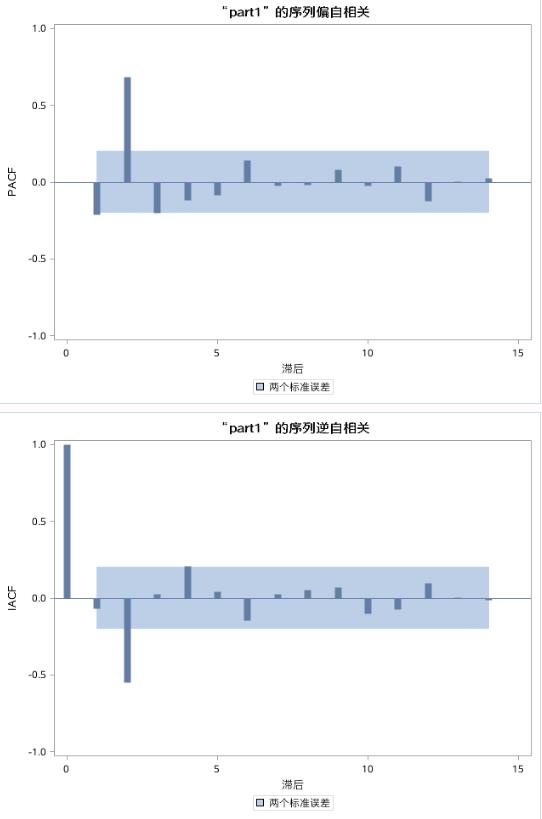
图17.37 例17.8中序列PART1的偏自相关图和逆自相关图
PACF图和IACF图具有一定的截尾特征（如图17.37所示），在2阶延迟处显著不为0，和AR（2）的特征相符。结合ACF图的特征，或许也可以尝试ARMA混合模型。
IDENTIFY语句也同时对part1的序列进行了白噪声检验，输出内容如图17.38所示。
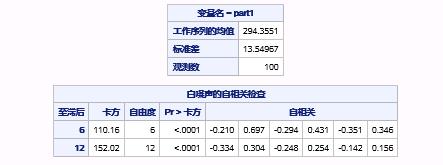
图17.38 例17.8中序列PART1的白噪声检验
这说明序列的观测之间存在显著的依赖关系，可以建模。
接着，由于使用选项ESACF、SCAN和MINIC进行了自动模型识别，系统输出了广义自相关系数矩阵及相应的P值矩阵、典型相关估计矩阵和卡方统计量的P值矩阵，以及MINIC方法的信息准则矩阵，并基于对这些矩阵的分析，提供了待选模型组，如图17.39所示。
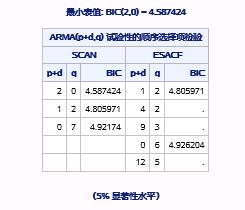
图17.39 例17.8中序列PART1自动识别出的待选模型
MINIC方法推荐的待选模型是AR（2）。假定序列是平稳的，SCAN方法推荐的待选模型为AR（2）和ARMA（1,2），ESACF方法推荐的待选模型有ARMA（1,2）、ARMA（4,2）等。当d>0时，也可以得出一些待选的非平稳模型。结合相关系数图，我们可以先将AR（2）作为part1序列合适的待选模型。
用同样的方法可以分析part2序列和part3序列，代码如下：
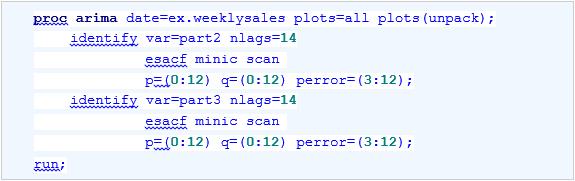
AR（1）和MA（3）分别是适合part2和part3序列的待选模型。
接下来，进行参数估计和诊断检验，查看用这些模型是否足够拟合这些序列。代码如下：
序列part1的参数估计和诊断结果如图17.40和图17.41所示。
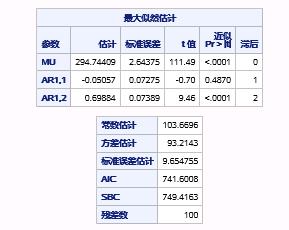
图17.40 例17.8中序列PART1的AR（2）模型参数估计和拟合优度报表
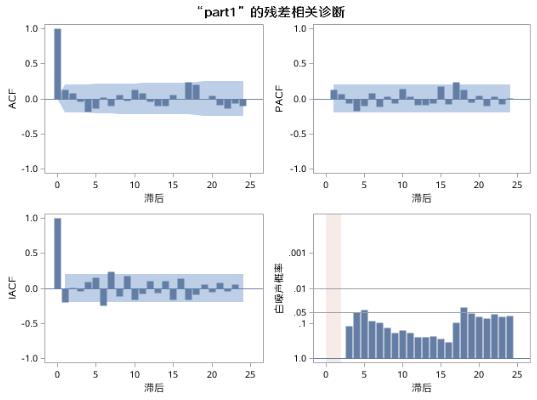
图17.41 例17.8中序列PART1的AR（2）模型残差诊断
从图中展示的结果可以看到，参数AR1,1的p值为0.4870，说明该参数不是显著非0；并且残差序列在5阶延迟时，p值小于0.05，说明残差序列不能通过白噪声检验，残差序列中仍然有信息没有被充分提取。因此，AR（2）模型对于序列part1是不合适的。我们可以尝试使用AR（3）。代码如下：
参数估计和诊断检验的结果如图17.42和图17.43所示。
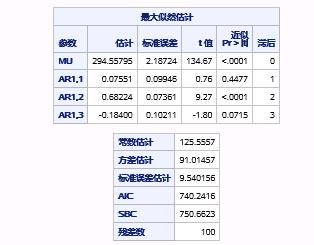
图17.42 例17.8中序列PART1的AR（3）模型I参数估计和拟合优度报表
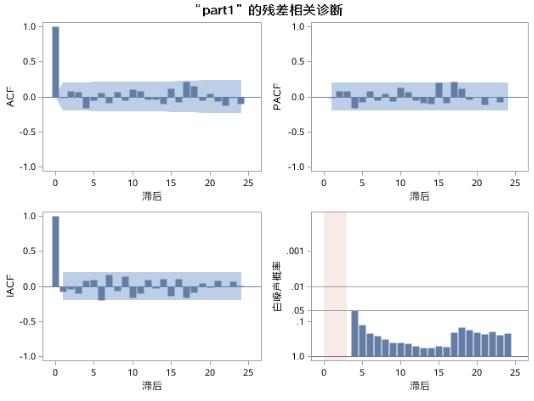
图17.43 例17.8中序列PART1的AR（3）模型I残差诊断
此时，残差序列基本可以通过白噪声检验，但是参数AR1,1仍然是不显著的。因此，可以考虑剔除AR1,1，重新拟合模型。代码如下：
选项p=(2 3)表示只使用2阶和3阶自回归项。参数估计如图17.44所示。
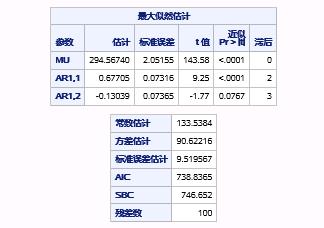
图17.44 例17.8中序列PART1的AR（3）模型II参数估计和拟合优度报表
这里，参数AR1,1表示2阶自回归项的参数，AR1,2表示3阶自回归项的参数，并且这些参数都是显著不为0的。
诊断检验的输出内容如图17.45和图17.46所示。
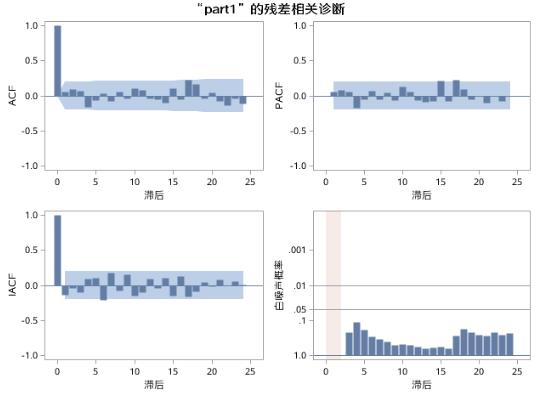
图17.45 例17.8中序列PART1的AR（3）模型II残差诊断
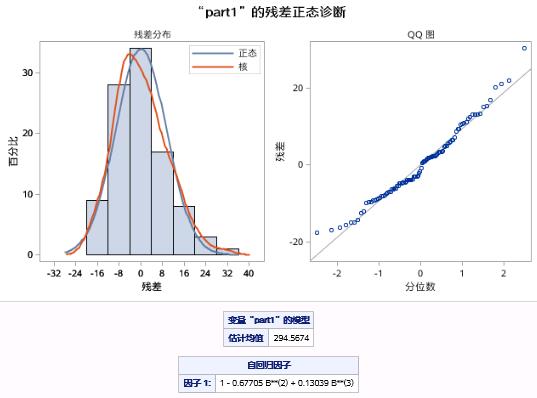
图17.46 例17.8中序列PART1的AR（3）模型II残差正态诊断
这说明使用只包含2阶自回归项和3阶自回归项的模型来拟合序列part1是合适的。
同样的方法，可以用来拟合序列part2和part3，得出适合part2和part3的模型分别为AR（1）和MA（4）。
接下来，就可以用拟合好的模型进行预测了。代码如下：
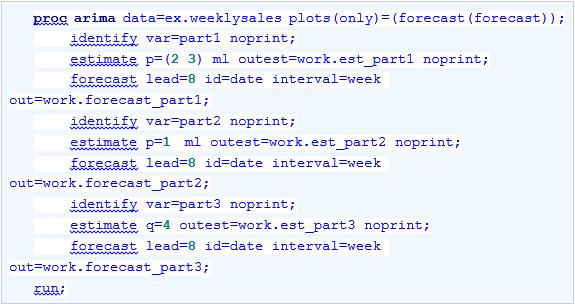
选项OUT=指定输出的预测结果分别被保存在数据集work.est_part1、work.est_part2和work.est_part3中。输出数据集work.forecast_part1中依次保存了ID变量（Date）、实际序列观测值（part1）、序列预测值（“part1”预测）、预测标准误差、95%置信下限、95%置信上限及残差，如图17.47所示。
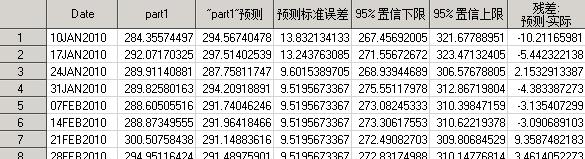
图17.47 数据集work.est_part1部分内容
系统输出如图17.48至图17.50所示的预测效果图。
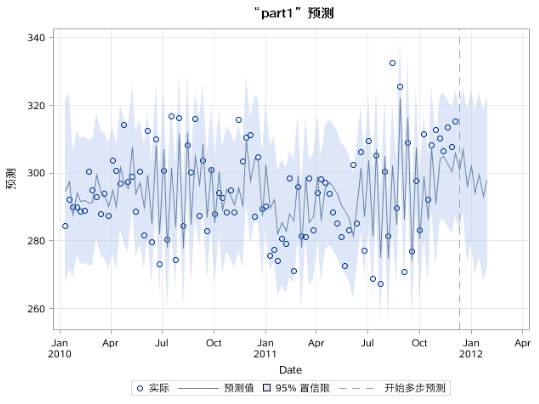
图17.48 序列PART1的AR（3）模型II预测效果图
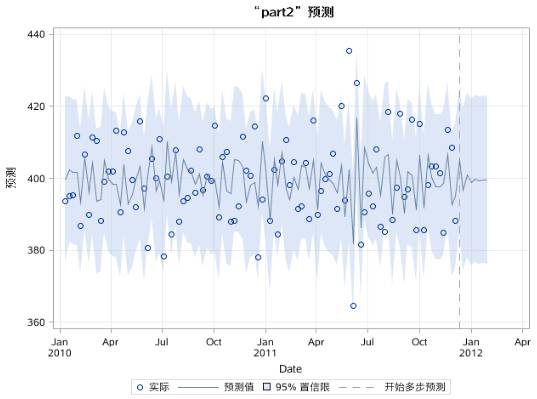
图17.49 序列PART2的AR（1）模型预测效果图
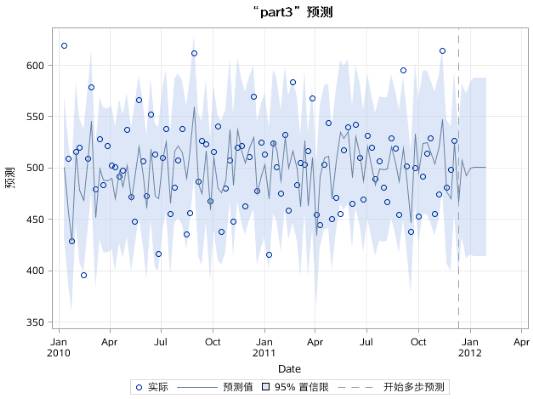
图17.50 序列PART3的MA（4）模型预测效果图
可以看到，part2和part3的预测在两周之后收敛到均值。
平稳时间序列是时间序列中一类重要的序列，可以说，平稳时间序列分析是时间序列分析的基础。在本节中，针对平稳时间序列进行了介绍，并结合实例介绍了Box-Jenkins时间序列分析的基本步骤：数据准备→平稳性和白噪声检验→模型识别→参数估计和诊断检验→预测。需要指出的是，在实际操作中，很多序列都不是平稳序列，它们有的是带有趋势的，有的是带有季节性因素的，那么遇到这种类型的序列时，我们该如何进行分析呢？
大量的经验证据表明，经济分析中涉及的大多数时间序列是非平稳的，特别是宏观经济时间序列，往往呈现出随时间而变化的趋势。非平稳序列的时间趋势主要有两种，一种是确定性时间趋势，一种是随机性时间趋势。
确定性时间趋势
所谓确定性时间趋势，从直观意义上讲，是指序列的趋势不是变化莫测的，可以用趋势线来加以刻画，用统计学的语言来描述，就是指序列的趋势是时间t的函数。
对确定性趋势的时间序列进行建模的方法为趋势拟合法，就是把时间作为自变量，相应的序列观察值作为因变量，建立序列值随时间变化的回归模型的方法。常见的趋势拟合函数有：
l线性函数
如果长期趋势呈现出线性特征，那么可以用线性模型来拟合它，模型可以具体写为：
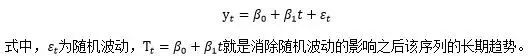
二次函数
如果长期趋势呈现出二次函数的特征，那么可以用二次函数来拟合它，模型可以表示成：
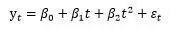
对数函数
如果长期趋势呈现出对数函数的特征，模型可以表示成：
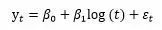
指数函数
如果长期趋势呈现出对数函数的特征，模型可以表示成：
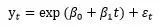
在ARIMA过程中，可以将趋势变量作为输入变量引入模型，进行确定性趋势拟合，基本语法为：
其中，在IDENTIFY语句中，选项CROSSCORR=在括号中指定和分析变量相关的输入变量，CROSSCORR可以简写为CROSS。如果在输入变量的后面指定了差分阶数，则系统将分析差分后的输入变量，如果同时在ESTIMATE语句用选项INPUT=指定了该输入变量，系统将使用差分后的输入变量进行模型拟合和估计。
例17.9：运用ARIMA过程进行确定性趋势拟合。
首先，用如下程序生成一组趋势时间序列。
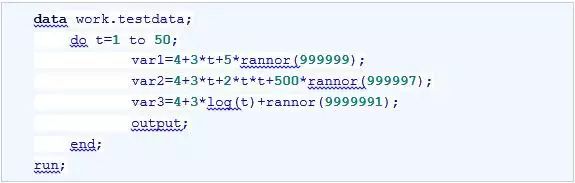
由于需要使用ARIMA过程进行确定性趋势拟合，因此，需要在输入数据集work.testdata添加趋势变量。代码如下：
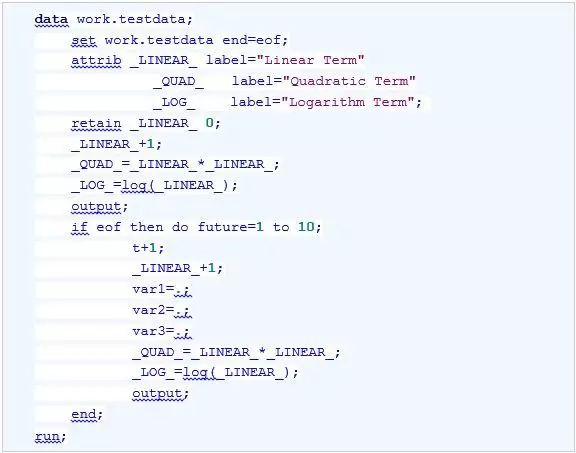
这里，新生成了变量_LINEAR_、_QUAD_和_LOG_，这些变量将进入ARIMA过程中对序列进行拟合。我们也注意到，在输入数据集的尾部，增加了10条新的观测，这10条新观测中，趋势变量都是非缺失值，序列VAR1、VAR2和VAR3都为缺失，等待ARIMA过程根据趋势变量进行拟合和预测。进行拟合和预测的代码如下：
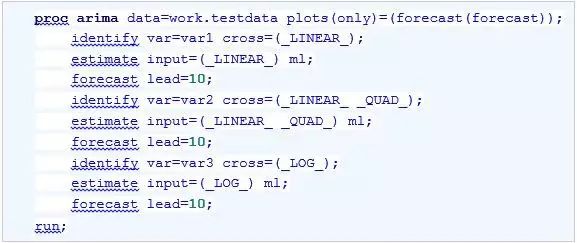
通常上面的代码，将得到拟合效果，如图17.51至图17.53所示。
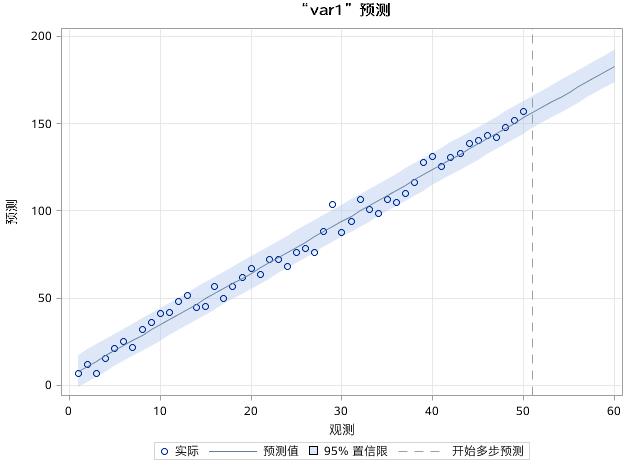
图17.51 例17.9中序列VAR1的预测效果图
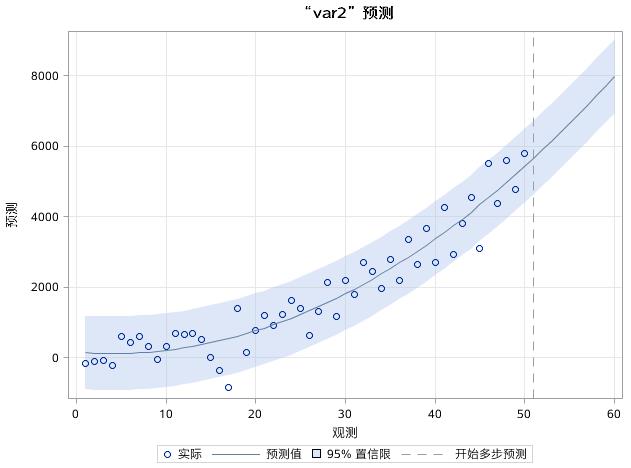
图17.52 例17.9中序列VAR2的预测效果图
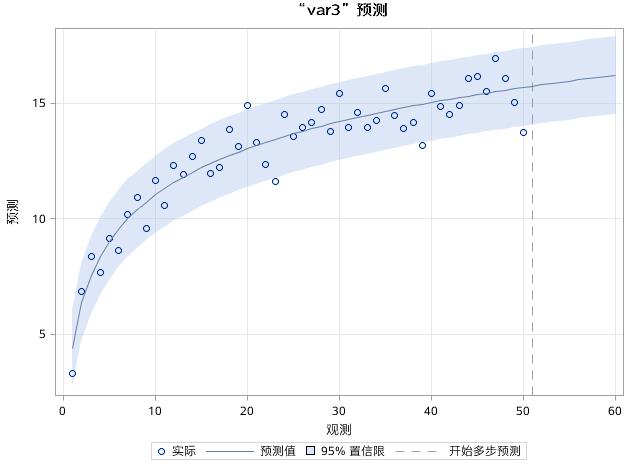
图17.53 例17.9中序列VAR3的预测效果图
运用趋势拟合法，可以将时间序列中的确定性时间趋势提取出来。如果时间序列在去除确定性时间趋势后，变成平稳时间序列，那么这种时间序列也叫做趋势平稳序列。对于趋势平稳序列，我们可以在提取出确定性趋势之后，运用Box-Jenkins方法进一步提取观测之间的依赖性关系。
风险提示：私募工场ID：Funds-Works所载信息和资料均来源于公开渠道，对其真实性、准确性、充足性、完整性及其使用的适当性等不作任何担保。在任何情况下，私募工场ID：Funds-Works所推送文章的信息、观点等均不构成对任何人的投资建议，也不作为任何法律文件。一切与产品条款有关的信息均以产品合同为准。私募工场ID：Funds-Works不对任何人因使用私募工场ID：Funds-Works所推送文章/报告中的任何内容所引致的任何损失负任何责任。
·END·
私募工场 ID：Funds-Works
以上是关于时间序列基本概念的主要内容，如果未能解决你的问题，请参考以下文章