时间序列 × 交叉检验

Posted 2021-05-02 统计译文

似乎我们已经很习惯于用交叉检验来进行模型优选了，但时间序列就因为其潜在的自相关性与非平稳性，让我们在交叉检验中做时序预测时顾虑重重。今天统计译文将整合来自两位时间序列专家Rob J Hyndman和Zach Mayer有关时间序列交叉检验的多篇研究，并分享给各位。

每个统计学者都知道，模型拟合优度(如R suqare)会随着模型的自由度的提升而膨胀；当用某个因为有很多参数导致拟合优度满分的模型（例如多项式回归）放到新的数据集上进行有预测，结果还一样表现优异吗？难说一种衡量预测效果的方法就是交叉检验：把原始数据拆开两份，一份称为训练集，用于拟合各种模型；再用另一份称为测试集的数据来衡量模型的预测准确性。

似乎我们已经很习惯于用上述的方式来进行模型优选了，但时间序列会存在潜在的自相关性与非平稳性，因此当我们把交叉检验的思路运用到时序预测时，就需要做一些分类讨论了：自回归模型和时间序列模型。

自回归模型

---

虽然传统的交叉检验在处理时序预测时并不稳健，但要是把经典的k-fold交叉检验套在自回归模型上，却在理论上可行^[1]。这对于经常用机器学习处理时间序列预测的朋友而言是一大福音。

自回归模型，顾名思义就是用该变量以前的观测值 (即滞后项，lagged terms)，来预测该变量本期的表现情况：

Y_t= Φ₀ + Φ₁y_t-1 + Φ₂y_t-2+ ··· + Φ_py_t-p + e_t

其中Φ₀是常数项，Φ1,...,Φp是模型参数， et是均值为0，方差为σ的白噪音；yt-1,...,yt-p是Yt的p个滞后项。

有关自回归模型的更为详细介绍，可以阅读过往文章：

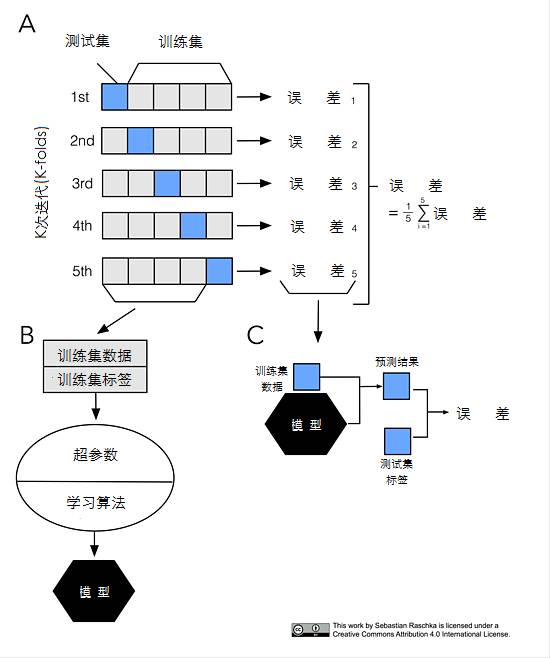
k-folds交叉检验示意图

按照自回归的思路在生成滞后项后，即可在k-folds交叉检验下使用各种回归算法完成模型优选工作。R语言中的某些包已经能协助我们完成上述自回归模型交叉检验任务，如forecast包中的tsCV()，caret中的createDataPartition()。

时间序列

---

用于时间序列预测工作的一些典型方法，如arima，ets，在做交叉检验时就要考虑到时间序列潜在的自相关性，即不能满足观察值的独立同分布，更不说时间序列建模还要考虑时间序列统计特性是否严平稳的问题。因此处理时序预测的交叉检验时，需要特别的交叉检验方法。

在说明这种特别的交叉检验方法前，需要先谈谈一种叫“弃一法”(leave-one-out cross-validation, LOOCV)的交叉检验；因为这两者相似度较高：

1. n个样本的数据集，抽取第i个样本(i = 1,...,n)作为测试集，剩下n-1个样本作为训练集；通过训练集所得模型匹配测试集计算预测误差.

    

2. 重复上述步骤n次，直至样本中的每一个样本都被放入过测试集.

    

3. 计算衡量总体误差的指标.

   
   

有批评指出“弃一法”交叉检验的结果可能有多个^[2]，就是说如果有一个“真”的模型，“弃一法”并非每次都能找到。但Rob J Hyndman倒不觉得这是“弃一法”的致命弱点，毕竟世界上有什么是永恒不变的呢？

介绍完“弃一法”交叉检验后，就来介绍处理时间序列建模的交叉检验——Moving Block Cross Validation，有人称之为“滑窗法”。“滑窗法”的概念很简单：

1. 从长度为m的时间序列中，抽取第1至第n个观察值作为训练集，第n+1个观察值作为测试集，通过训练集所得模型匹配测试集计算预测误差.

    

2. 完成上述步骤后，训练集与测试集均往前挺进1个观察值，再重复上述步骤，直至时间序列的第m个观察值也被测试集所取值后，该循环结束.

    

3. 计算衡量总体误差的指标.

一图蔽之即如下：

“滑窗法”交叉检验示意图

“滑窗法”的变体跟上述介绍大同小异：例如测试集的长度，即每次训练集向前挺进的步长h，可以不仅仅是1。再例如测试集是要固定的长度呢，还是会通过吞并测试集来增加长度？这两者就是Rolling / Non-Rolling的区别了。“滑窗法”的概念可以追溯至上世纪八九十年代的一系列讨论^[3]，考究党可以查阅他们的工作。

提供时序预测交叉检验的R包有如cv.ts包，forecastHybrid等；boot包中的tsboot()则提供Moving Block Bootstarp实现函数，类似的包还有meboot，timesboot，BootPR；在python中有TimeSeriesSplit可以完成类似任务。

实际上除了时间序列外，还有一些类型的数据是常常无法满足独立同分布假设的，例如经管社科领域常见的存在嵌套层级的数据（如学生水平嵌套于班级水平，班级水平嵌套于学校水平），空间统计学里常处理的数据（如某区域经济水平容易受到临近区域的影响）等等。因此在使用各种方法前，还需考虑该方法的适用条件。

参考

---

[1]. Bergmeir C, Hyndman R J, Koo B. A Note on the Validity of Cross-Validation for Evaluating Time Series Prediction[J]. Monash Econometrics & Business Statistics Working Papers, 2015.

[2]. Jun Shao. Linear model selection by cross-validation. Journal of the American Statistical Association, 88(422):486-494, 1993.

[3]. Hans R. Kunsch. The Jackknife and the Bootstrap for General Stationary Observations. The Annals of Statistics Vol. 17, No. 3 (Sep., 1989), pp. 1217-1241

---