算法 | 时间序列,无法绕过的平稳模型ARMA
Posted 擎创夏洛克AIOps
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法 | 时间序列,无法绕过的平稳模型ARMA相关的知识,希望对你有一定的参考价值。
对于夏洛克ITOA来说,进行异常检测、容量预测等处理分析,都绕不开时间序列
而时间序列的算法,则绕不过平稳模型
时间序列第一篇请戳 :
本文将介绍第一类非常重要的模型:自回归滑动平均模型(ARMA)。在真实案例中,ARMA模型也被高频的使用到,更是后面模型的基础,反正,时间序列是绕不过去ARMA模型的。
2.1 一般线性过程
ARMA模型属于一大类过程(模型),即一般线性过程。一听到线性过程,是不是就觉得不难了? 事实也是如此,别怕,干!
那什么叫线性过程呢?对一时间序列 { Yt } ,比如就是2017年06月 27日的上证指数。则其可表示成现在与过去白噪声的加权线性组合:
其中 { et } 代表白噪声序列,为一实数列(可认为 ψ0为1) 。考虑到收敛问题,需加一个限制条件:
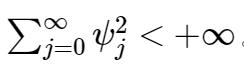
2.2 滑动平均过程
2.2.1 一阶滑动平均过程
在介绍ARMA模型前,先介绍一些它的简化版本,这样循序渐进,慢慢深入,痛苦也会少一点,快乐也就多一点。
最先介绍的当然是滑动平均(Moving Average, MA),而且是滑动平均的最简版:一阶滑动平均。
对于一阶滑动平均{
通常称{X~t~} 为 MA(1) 序列。
接下来要探讨统计特征啦(以后,再学习一些模型时,都会经历这一步。其实这才是重点啊,因为这些特征告诉我们模型的特性,那也就暗示了模型的应用场景啊!当然,==从应用的层面,也不需要你知道怎么推导,故只需关注每个公式最后的等号就可以了==,当然如果想加深理解、记忆,每个公式仔细看是有必要的)
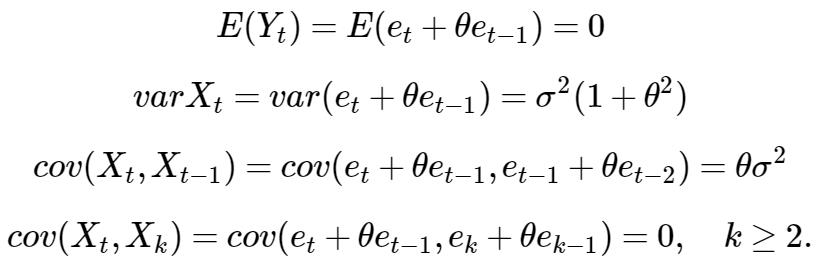
因此,对于MA(1),自协方差函数γk和自相关系娄ρk
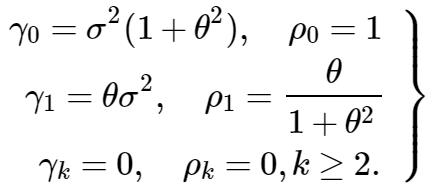
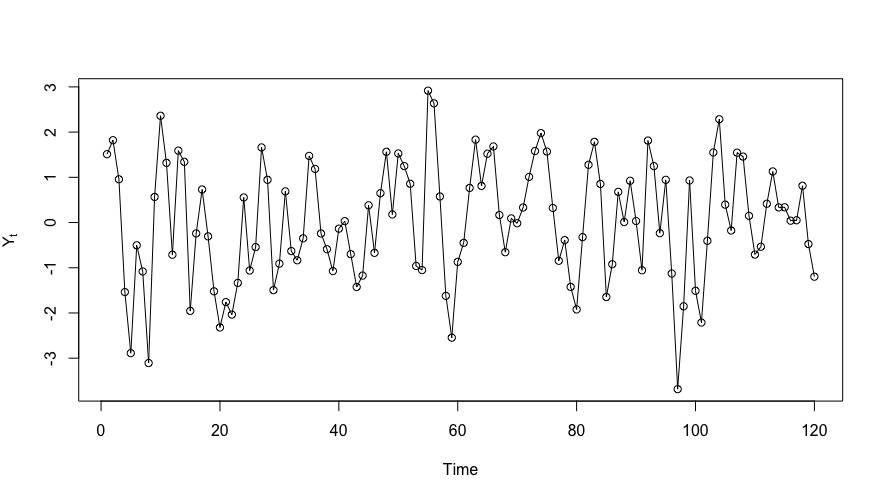
2.2.2 q阶滑动平均— MA(q)序列
任给定q个实数θ1,θ2,...,θq (θq≠0),则MA(q) 序列{
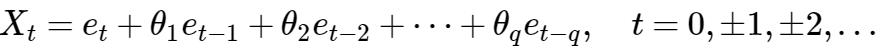
可见,MA(q)与MA(1)是非常类似的,只不过有变得繁琐而已(注意,是‘繁’不是‘难’)。
比如处协方差函数
γk
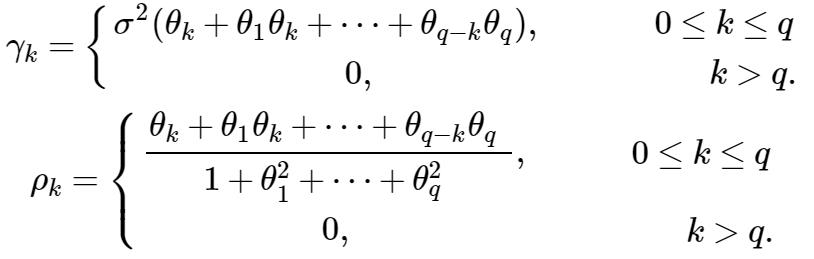
为使上面的等式可识别(‘可识别’ 可简单的理解为参数可估)需加一些限制,比如:
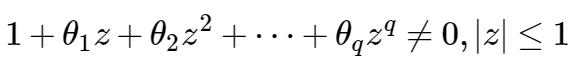
当然,这个条件对等式成立本身没有影响,只是为了参数可识别而已,对于应用来说,其实可忽略,因为实际应用时,默认参数可识别,如果最终结果不符,我们就会换到其他模型了(尴尬~)。这也是学院派与经验派(或务实派)的一个区别吧。
2.3 平稳自回归过程
另一个ARMA的简化版即为自回归(Auto Regression,AR)过程。如MA我们先介绍一阶自回归(AR(1))开始。
2.3.1 一阶自回归过程
对于一阶自回归序列 { Xt} (AR(1)):
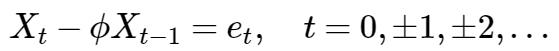
其中白噪声{
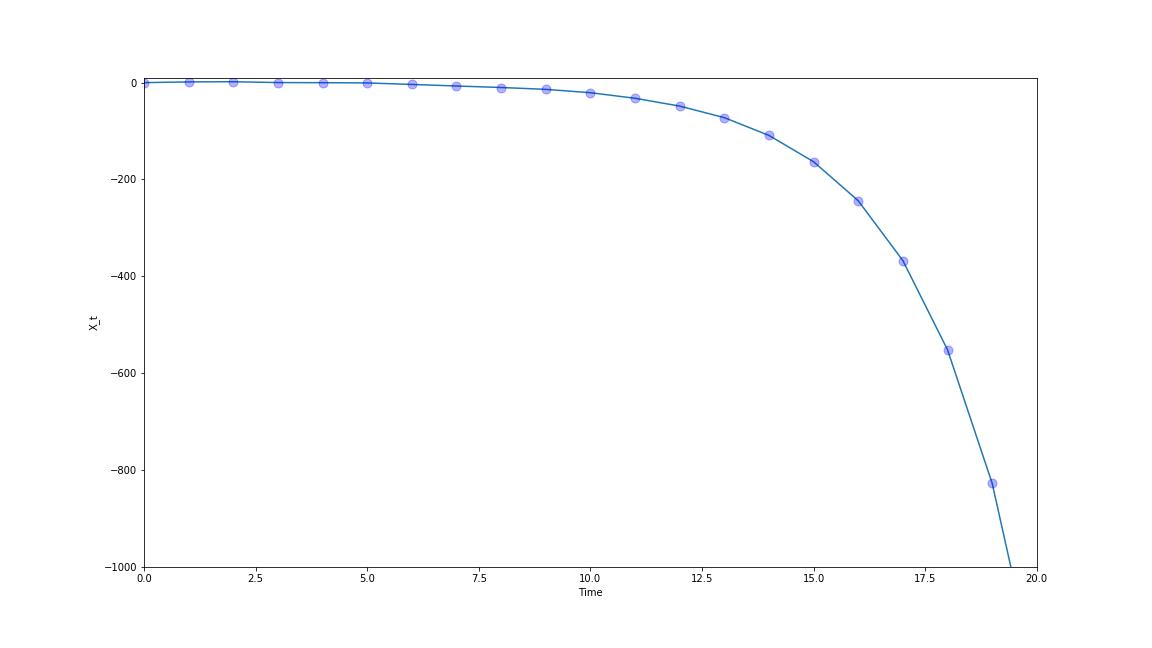
上图可以看到,t 还没到20, X~t~ 已经达到-1000了。
正如刚刚提到,AR序列类似等比数列:
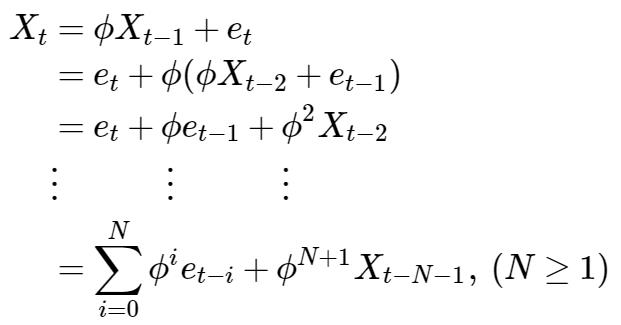
注意,这里还是要求
于是:
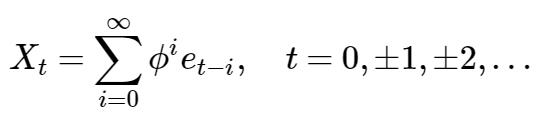
故,{
对(9)式可写成:
Xt = ϕXt-1 + et
对两边求方差即可得到:
γ0=
对γ0 求解:
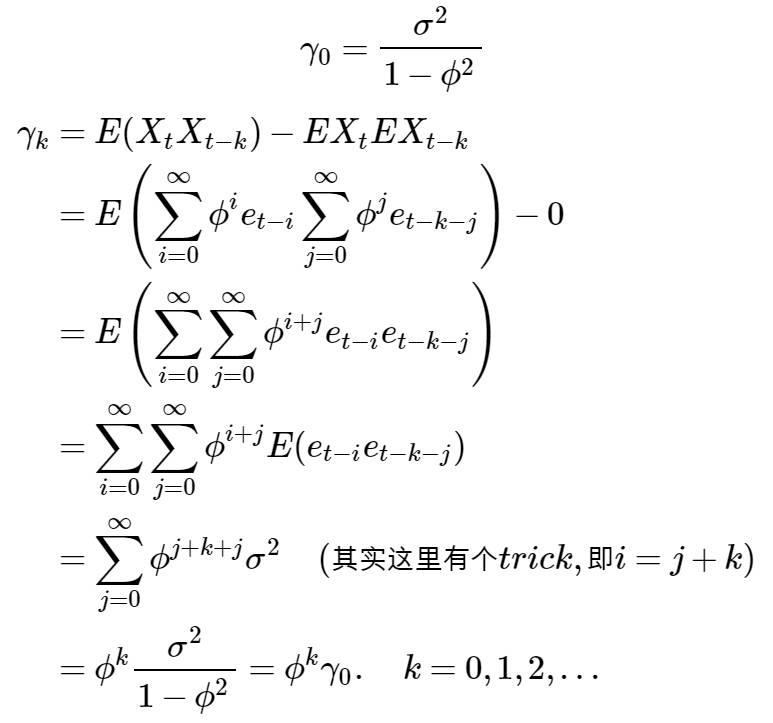
再强调一遍,如果只是想了解下时间序列,只是想应用,那就只关注等式的最后一个等号就可以了。
上式为自协方差函数,根据γk,可求得:
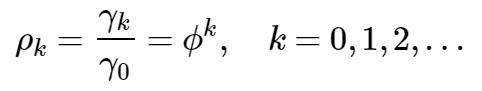
2.3.2 p阶平稳自回归序列
怎么样,公式有点多,醉没醉?可以休息下再看,什么再来一壶,OK!AR(p)继续!
AR(p)序列
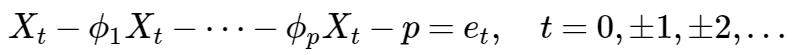
其中
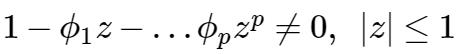
对于线性表示,经过‘不太复杂’的推导,可得:
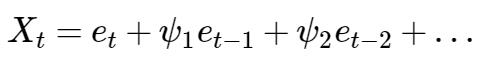
其中系数 { φj:j=1,2,…} 由下式确定:
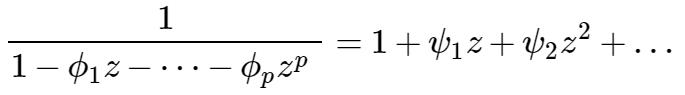
利用{ Xt}的线性表式(16)式,可得一个重要等式:
E(Xt-ket)=0, k=1,2,...
下面来求解AR(p)序列的自相关系数 ρk:
在(15)式两边同乘 Xt-k,(K≥1)

两边同求数学期望:
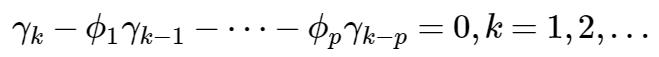
同除 γ0,
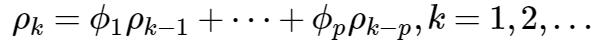
分别令
k=1,2,…,p
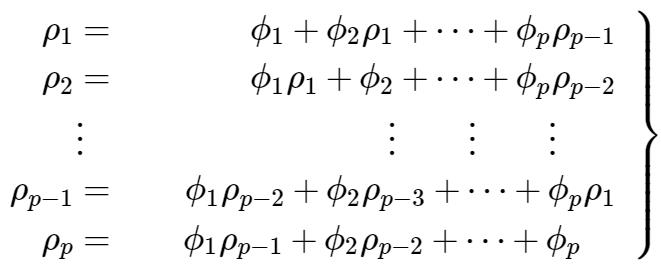
这就是著名的Yule-Walker方程。
上式写成矩阵形式更方便记忆:

全是公式?!怎么搞?!举了例子呗:
例:设AR(2)序列{X~T~}:
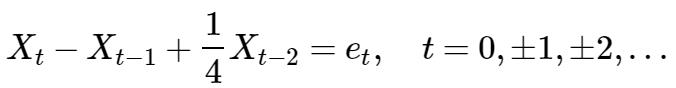
其中{et} ~W N(0,1)。试求 {Xt}的自相关系数
解:
可知:Φ1=1,Φ2=-1/4
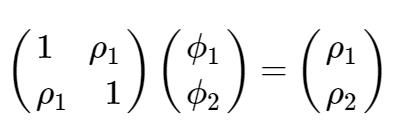
解得:
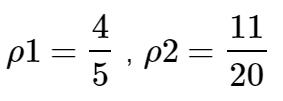
对时间序列建模,我们一般是要求回归参数
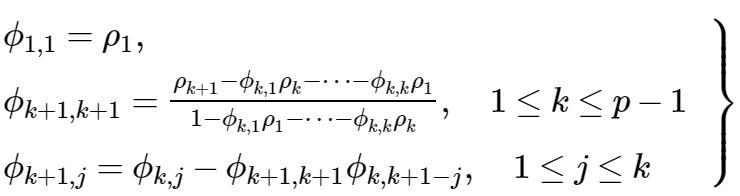
2.4 平稳自回归滑动平均序列
Finaly, 终于到了自回归滑动平均(Auto Regression Moving Average,ARMA(p,q))序列{ Xt},当然上面也都是ARMA序列,只不过是简化版本而已。
ARMA(p,q)序列是满足下面差分方程的序列(参数意义同上):
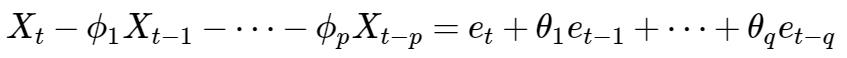
为了可识别,需有些限制条件:

2.5 总结
这回探讨了ARMA(p,q)模型,这个模型其实还是基础模型,但我与大家同感,尽管是基础模型,可还是很复杂,没办法,时间序列这一数据类型决定了其相关的模型是不平凡的。
不过,也不用担心,虽然公式多了点(是在我尽力规避不必要公式后,还有这么多),你只需要知道每个公式最后的等号就好了(这是第三遍了,足见其重要!)。
模型逻辑还是清晰的,AR,MA,弄懂,ARMA可简单理解成二者的合并(虽然推导方式不一样了),这样便于理解。模型阶数实际中一般不会很大,所以也不用担公式复杂,不易应用。
最后一句: Hold住,也许下一个改世界的人就是你。
夏洛克 ITOA
为企业量身定制的IT运维专家
人工智能 | 机器学习 | IT运维
以上是关于算法 | 时间序列,无法绕过的平稳模型ARMA的主要内容,如果未能解决你的问题,请参考以下文章