时间序列

Posted 2021-05-02 万鱼同跃

以时间为横轴，选取某个指标，一个人都可以看成一条曲线，画出来的部分已经不可改变，还没画出来的部分又充满了不确定性。

 

这么一条曲线其实是连续变化的，数学上可以看做一个（随机）过程，但是连续的东西不方便研究，于是先离散化，每隔一段取一个点，得到一连串的数据点组成的数列，就是（随机）序列，（离散化了就叫“序列”），又因为以时间为下标，所以叫时间序列。比如，取我的体重为指标，从我出生开始每隔一年取一个数据，由此得到的有顺序关系的22个数据组成的数列就是一个时间序列。还有比如中国1962~2016年的GDP，北京2000~2015年每个月的PM2.5等等都是时间序列。

 

通过时间序列，人们往往想研究一个指标随时间变化的规律，最好能表示成时间的确定性函数的形式，比如一辆匀速行驶的小汽车t时刻离起点的距离X_t就是关于时间的简单的线性函数X_t=vt,其中v是速度。但是一个醉汉走了第t步时离起点的距离X_t就不能表示成时间的确定性函数了，他每一步迈出的步长有长有短，也有可能是往后走的，即是随机的，但第t步时离起点的距离X_t还能通过前一步的距离X_t-1来表示， 即X_t= X_t-1+e,这里e是随机的，不确定的。其实匀速小汽车的例子也可以表示成这种形式：X_t=X_t-1+ v[t-(t-1)].这里多出来的那一项不是随机的，是确定的。

 

如果学过概率论，应该记得一个最有名的分布叫正态分布，我们假设e服从标准正态分布N(0,1)，根据X_t=X_t-1+e，醉汉前500步走出来的距离可能是这样的：

图1

也可能是这样的：

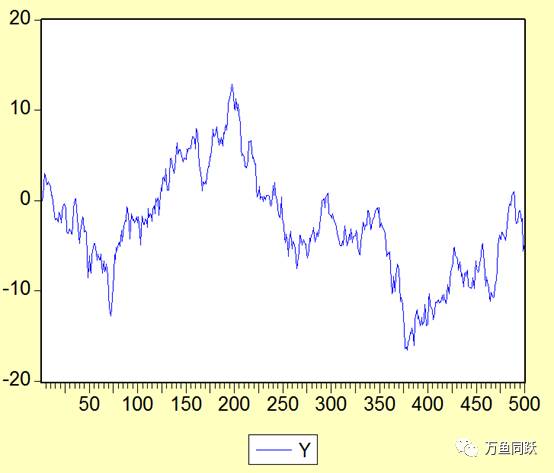
图2

可以看到，这两个不同的醉汉最远都没有超过20,500步之后还在起点附近。

 

假如这个醉汉醉的没有这么厉害，每一步至少往前走了一点点（比如0.1），然后再随机，X_t= X_t-1+0.1+e，刚才的两幅图就变成了：

图3

图4

可以看到，图3中的这个人前200步还看不出什么变化，200步到500步的时候开始一直上升了，图4中的这个100步到200步有一个上升，200步到400步上下震荡，400步到500步有有了一个上升。

 

其实这和每天持续行动很像，没有坚持每天做一点的人，就和前两个醉汉一样，时好时坏的，过了500天大概一年又4个月的时间吧，和最开始没什么区别。

但是每天坚持的人，可能那个质变的时间有早有晚，或者后来又遇到了瓶颈什么的，但是到了500天都达到了一个不错的高度。

 

当然啦，实际情况可能不是这样的模型，参数也不一样，以至于我最后的结论也有可能是错的，但是，让我先坚持到500天再说吧。