时间序列第二弹广义自回归条件异方差模型GARCH

Posted 2021-05-02 研模时光

第一部分：背景介绍

前面两期，我们推送了自回归滑动平均（ARMA）模型的理论和一个实例，ARMA模型可以对资产收益率序列本身进行建模，因此称之为“均值模型”。那么，对收益率的方差或者标准差序列能不能进行建模呢？答案是可以的。这就是时间序列模型里面经常出现的广义自回归条件异方差模型（GARCH），在金融中也称之为“波动率模型”。关于GARCH类模型的文献综述起源于Engle（1982）关于金融资产收益率序列的条件异方差性（Conditional Heteroskedasticity）的研究，提出了自回归条件异方差模型（AutoRegressive Conditional Heteroskedasticity，ARCH）。条件异方差性是指在以前信息集下，一个时间序列服从某一连续分布（如正态分布、学生t-分布等），该分布的均值为零，方差是一个随时间变化的量(非常数，即为条件异方差)。Bollerslev和Taylor（1986）将Engle的ARCH模型扩展到GARCH模型，即最常用的广义自回归条件异方差模型（Generalized AutoRegressive Conditional Heteroskedasticity，GARCH）。

和以前一样，我们还是先来介绍一下提出这个模型的学术大师们。Engle(1982)在Econometrica杂志的论文：Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation中，首次提出ARCH模型可以说是GARCH类模型的开拓者。2003年他因为提出这个模型而获得了诺贝尔经济学奖。下图的左边就是Engle，右边就是Bollerslev：

---

第二部分：资产波动率的特征

GARCH类模型用来刻画金融资产的“波动性”，一个金融资产的波动率（即收益率的标准差）不能通过市场进行直接观测到，但是它有以下几个特征很容易看到：（1）存在波动率聚集现象（Volatility Cluster），就是说波动率在一段时间内高，而在另一段时间内低；（2）波动率往往是平稳的，波动率不发散到无穷，它是在固定的范围内变化；（3）波动率是连续的，即随着时间的变化，波动率很少有跳跃的现象；（4）存在杠杆效应（Leverage Effect），即波动率对价格大幅上升和价格大幅下跌的反应不同。GARCH类模型就很好地刻画了波动率的这些特性。

---

第三部分：GARCH模型表达式

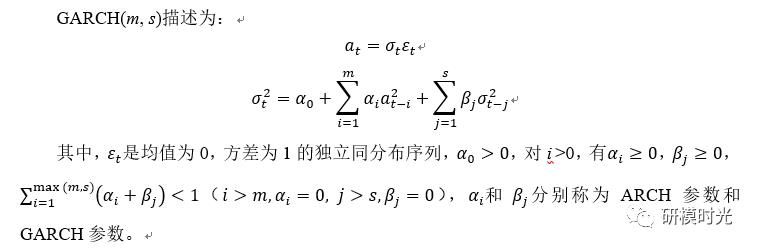
其中的at就是我们之前用ARMA模型拟合的残差项，它是一个平稳噪声（正态分布、学生t-分布等），且其均值为0，标准差为sigma，我们以后会介绍用不同的分布类型来对残差进行拟合，选择最好的拟合模型。那么et等于at除以sigma，其实就是一个标准的平稳噪声（均值为0，方差为1）！下面的关于sigma的方程就是一个波动率方程了，它与滞后m项的at平方，以及关于自身滞后s项进行回归就得到了GARCH模型。可以看到sigma的前几期对当前期有影响，前几期越大，则当前期就越大，前几期越小，则当前期就越小，正不就正好是波动率的聚集现象吗？

在GARCH模型之后，很多学者提出了数不清的对GARCH模型的改进模型，如GARCH-M、IGARCH、FIGARCH、EGARCH、FIEGARCH、TGARCH等等，都是为了更好地刻画前面提到的波动率的四个特性。GARCH类模型的具体表达式就不一一列举了，其发展过程为：

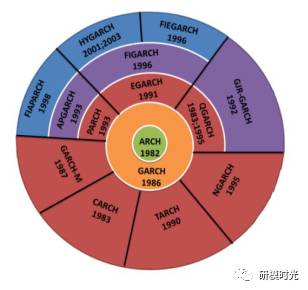
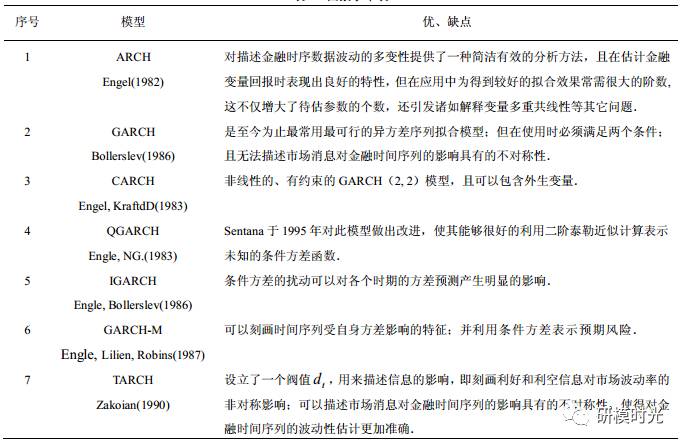
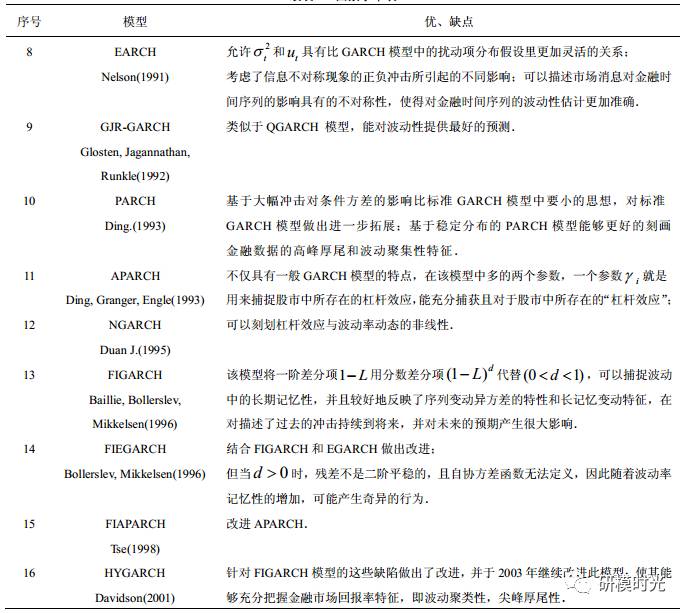
这个图截自（徐洁，GARCH 模型发展研究综述，Scientific Journal of Mathematics Research）

---

第四部分：建模过程

ARCH效应检验

在对时间序列进行GARCH模型建模时，必须先要进行序列的ARCH效应（即条件异方差性）检验。如果模型的残差序列没有条件异方差性，那也就不谈GARCH模型了。这里的残差序列可以由ARMA模型的残差得到。由于条件异方差性就是序列的残差均值为0，而方差随时间变动，因此其残差序列的方差就等于at^2，即残差序列的平方即为其方差。检验条件异方差性就可以对at^2进行Ljung-Box自相关性检验，如果它有自相关性，那么他就是非平稳的，可以推出它是异方差的！

另外，ARCH模型还可以表示为at^2的自回归形式（具体推导见Ruey S. Tsay 《Analysis of Financial Time Series, Third Edition》），因为自回归模型可以由其PACF进行识别（p步截尾），所以可以观察at^2的PACF看其是否有ARCH效应！

模型定阶

如何对一个GARCH模型进行定阶呢？即如何确定具体的m和s呢？前人的经验表明，拟合一个GARCH模型一般只涉及到很小的滞后阶数，一般是从GARCH（1,1）、GARCH（2,1）、GARCH（1,2）和GARCH（2,2）中进行选择，而GARCH（1,1）模型是用的最多的。我们可以用前面介绍的AIC和BIC信息系数对这四个模型进行选择，即选择系数最小的模型！一个GARCH（1,1）模型的具体形式为：

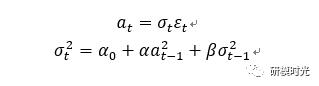
这个常用的形式是不是看起来简洁舒服得多！

GARCH模型的推导和性质远没有我写的这么简单，但是我们的目的就是为了实战，所以知道其原理、特性和用的方法就可以了！

---

第五部分：下期预告

下一期我们将会用Python的ARCH包对上证50ETF的对数收益率序列进行GARCH波动率建模，并对其进行一系列的检验和预测。然后将波动率预测的结果与上交所发布的中国波指（iVX）进行比较，然后尝试性地对上证50ETF期权的波动率交易进行参考。

---