时间序列模型拾遗1统计分布类型，黑天鹅的秘密？

Posted 2021-05-02 研模时光

之前的四期我们推送了时间序列ARIMA和GARCH类模型以及他们的实证研究，在介绍这些模型的时候提到了金融资产的对数收益率序列rt、ARIMA的残差序列at以及GARCH模型的标准残差序列et。最通常的情况下，都是假设这些序列服从一个已知均值和方差的正态分布N(u, sigma^2)。但是真实的分布类型是不是这样呢？

一个最普遍的共识是，对数收益率序列的分布特征是“尖峰厚尾”的。尖峰厚尾是指它比正态分布峰度要大，伴随的就是分布的尾部比正态分布高。此外，我们知道正态分布是关于均值u完全对称的分布，但是收益率序列的分布可能是有偏斜的，即它不对称。

---

一、峰度(Skewness)和偏度(Kurtosis)

一个随机变量的峰度和偏度的定义以及它与正态分布的偏度和峰度的关系可以归纳如下：

---

二、尖峰厚尾(Leptokurtosis and Fat Tails)

一般尖峰厚尾是相对于正态分布来说的，尖峰意味着实际分布中靠近均值的观测值数量多，比如对数收益率序列大部分都集中在0附近；厚尾意味着极端值的出现频率比正态分布高，即出现“黑天鹅事件”，比如2015年上半年A股出现一轮牛市，那段时间的股票收益率出现了很多极端大的正值，2015年8月份A股经历一轮股灾，那段时间的股票收益率出现了很多极端大的负值，这些正负极端值都是“黑天鹅事件”，分布在横轴的两端。下图给出了一个尖峰厚尾的直观展示，横轴可以理解为收益率序列值，纵轴可以理解为对应的值出现的频率：

---

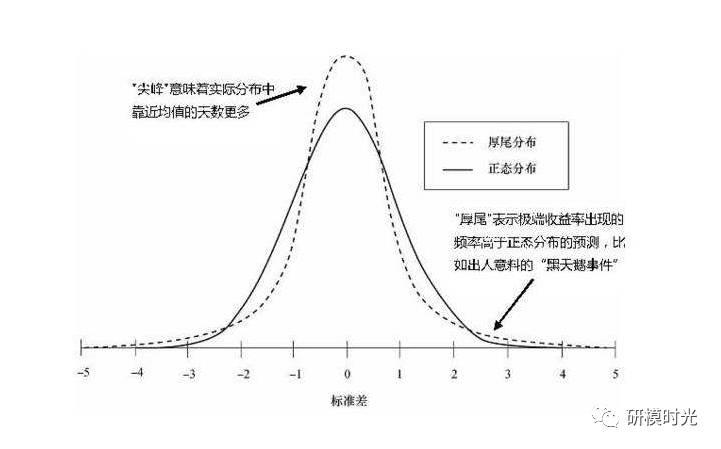
三、偏斜分布(Skewed distribution)

偏斜分布是指分布的峰值与平均值不相等的分布。根据峰值小于或大于平均值可分为正偏分布和负偏分布。如果某个股票的对数收益率序列的分布是正偏分布，则表示其正的收益率分布的更广，即正的极端值出现的更多；如果是负偏分布，则表示其负的收益率分布的更广，即负的极端值出现的更多。下图给出了偏斜分布的一个直观的图示：

---

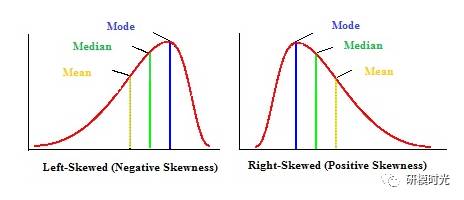
四、常用的尖峰厚尾和偏斜分布

微信打公式实在太丑，就先用Word打好，再转成图片发上来了。下面图片第一个学生-t分布和第二个广义误差分布是常见的尖峰厚尾对称分布，它们都有峰度参数可以控制分布的峰度；第三个是Fernandez和Steel (1998)提出的可以把偏度引入任何连续的单峰及关于原点对称的连续随机变量分布的方法。因此利用第三个变换方法，可以把对称的学生-t分布和广义误差分布变换为偏斜的学生-t分布和偏斜的广义误差分布，见第四个和第五个分布，它们都有偏度参数，可以控制分布的偏度。

---

五、下期预告

下一期，我们将对上证50ETF对数收益率序列以及GARCH模型的标准残差序列的峰度和偏度进行研究，并对其尝试拟合一个尖峰厚尾偏斜分布。还会用R软件强大的gamlss包的dist子包，即gamlss.dist，对上面的所有的分布进行统计模拟。

---