风险模型在时间序列上的改进 ——《系列之三十一》
Posted DigitalAlpha
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了风险模型在时间序列上的改进 ——《系列之三十一》相关的知识，希望对你有一定的参考价值。
核心结论：
1) 风险模型有三个功能：控制风险暴露、估计收益率协方差矩阵、绩效归因。不是所有功能都要用到风险因子，估计协方差矩阵可以采用纯统计方法，报告把这个领域最新学术成果和业界常用的因子模型在A股进行了实证对比。
2) 由于股票数量多，收益率样本数量少，样本协方差矩阵的估计误差比较大，导致其矩阵条件数（最大特征值除以最小特征值）较高，输入组合优化器进行数值求解时会让结果对数据误差十分敏感。压缩估计方法即是去调整样本协方差矩阵的特征值，压缩其分布区间，同时降低估计误差。我们之前研究中一直采用线性压缩方法(LS). 报告里新测试了Ledoit(2017)提出的非线性压缩估计(NLS)。
3) 因子模型(FM)的构建参考了BARRA CNE5 文档，在估计因子收益率协方差矩阵和特质方差矩阵时采用非线性压缩方法，并增加了EWMA时变结构。
4) 协方差矩阵估计也可以采用多元GARCH模型，但参数估计方法需要做大的改进。我们采用CL方法进行参数估计，BEKK和DCC GARCH模型已经可以较快估计出参数，具备实盘价值，但历史回溯太耗时，最后实证采用的是简化版的CCC-GARCH，股票数量较多时，它和DCC GARCH差别不显著。
5) 我们用不同协方差矩阵估计量构建全局最小方差组合（GMVP），看哪种方法得到的GMVP组合的真实方差最小，判断协方差估计量的优劣。
6) LS，NLS和不加时变结构的因子模型表现基本相当，差距在统计上不显著。鉴于NLS方法在仿真测试的优越性，我们预计横截面方向风险模型的改进空间可能很有限。
7) FM和CCC-GARCH表现显著比LS和NLS强，时间序列上改进风险模型的作用明显，把这两者等权组合在一起可以减小模型设定偏误，进一步显著增强模型风控能力，并降低组合换手。
8) 时间序列方向上改进风险模型的代价是增加组合换手。究竟是时变模型带来风险下降的利好多，还是换手率增加带来的损失多，取决于alpha模型、组合约束条件、产品规模、交易成本等因素，不同的问题可能会有不同的结论，但至少这是一个值得尝试的改进方向，特别是那些交易便利的机构。
http://pan.baidu.com/s/1mhHqm1a
以下为报告全文：
风险模型概述
如我们前期报告所述（《A股市场风险分析》，2016.12.02），风险模型的作用有三个:
1） 识别风险因子、控制风险暴露，降低组合净值波动；
2） 估计协方差矩阵，输入后续的组合优化器；
3） 绩效归因，分析组合风险暴露，收益来源；
鉴于BARRA在风险模型领域的领导地位，很多投资者在概念上会直接把风险模型等同于BARRA，BARRA提供了一系列实用性强的风险因子（参考MSCI CNE5 附录）来实现上述三个功能，其它公司，像Axioma、Northfield，也有提供自己的风险因子。BARRA CNE5 的风险因子和其之前公布的美国版本USE 4 比较类似，A股是否存在特有的风险因子值得研究。我们在之前报告中给出了一套风险因子定量判别方法，和alpha因子相比，两者最大的差别在于：
i. alpha因子看重的是时间序列方向上因子收益率的显著性，风险因子看重的是横截面方向上因子对股票收益的解释度，其因子收益率在时间序列上可能不显著；
ii. 风险因子在时间序列上数值要稳定，不能变化太快，否则风险控制起不到作用。alpha因子则不要求，只要其因子收益率能够覆盖高换手带来的交易成本即可。所以对于月频调仓组合而言，“过去一个月收益率”因子只适合做alpha因子，不适合做风险因子，因为一个月间隔后，这个因子的数值变化太过剧烈， 上次调仓做的风险控制不起作用。
风险模型的第二个功能不一定要用风险因子来做，有很多其它的统计方法。协方差矩阵估计领域的研究成果众多（Pourahmadi,2013），我们本篇报告重点关注的是这个领域专家Oliver Ledoit (http://www.econ.uzh.ch/en/people/postdocs/ledoit.html) 近些年提出的一些高效算法在实际投资中的作用，并和业界常用的类BARRA的因子模型做对比。
2
协方差矩阵估计方法
2.1 样本协方差矩阵的不足
假设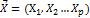
是一个p维随机向量，有n个观察值
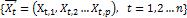，随机向量的协方差记为
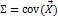。如果
满足p维正态分布，则 Σ 的极大似然估计正好等于样本协方差矩阵：
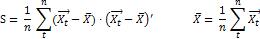
S 是一个无偏估计，如果 p 是一个不变的常数，则在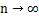
时，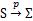
。不过在估算股票收益率协方差矩阵时，由于股票收益率的分布在时间序列方向上不稳定，不建议用太长的历史数据，所以经常碰到的情况是用过去一年252个交易日的数据去估算1000甚至更多只股票的协方差矩阵，样本协方差矩阵S的秩等于 n – 1，因此当p≥n时，S不可逆；即使 p <n,根据Ledoit(2004)里面的引理2.1，S特征值也会比 Σ 特征值的分布区间广，因此S特征值的最大值比Σ 特征值的最大值大，S特征值的最小值比Σ 特征值的最小值小，造成矩阵S的条件数（Condition Number, 矩阵最大特征值除以最小特征值）偏高，偏高幅度与p/n 的大小正相关。后续的组合优化过程中可能会对S求逆或者以S为系数矩阵求解线性方程，S条件数过大会让计算结果对数据误差十分敏感，使得组合优化得到的组合权重不稳定。
解决这个问题的常用方法有三种：
1） 增加样本数量n。前文提到不宜用太久之前的历史数据，因此可以考虑提高数据的采样频率，也就是采用高频数据。不过高频数据在增加样本数量的同时也在增加数据噪音，统计工具上可能要有所改变。另外高频数据计算得到的是高频协方差矩阵，高频数据在收益率序列自相关性和低频数据可能有差异，如何把高频协方差矩阵转换成低频协方差矩阵也是需要考虑的问题。
2） 降低变量维度p。BARRA因子模型属于这一类，也称作结构化风险模型。它通过寻找少量因子来解释股票收益率，把估计股票收益率协方差矩阵转换成估计因子收益率协方差矩阵和个股特质方差，把需要估计的参数数量从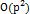
大幅降为O(p)，减小估计量的方差。因子对股票收益率的解释度越高，降维效果越明显。
3） 通过函数转换调整样本协方差矩阵的特征值，同时提高估计准确性。这也是下文要介绍的压缩估计方法。
2.2 线性与非线性压缩估计
首先介绍压缩估计量方法，这个在后面的因子模型里也会用到。对于p维对称矩阵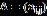
和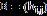
，常用Frobenius 距离来衡量两个矩阵的接近程度：
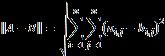
如果Σ 是要估计的真实协方差矩阵，
是某个协方差矩阵估计量，可以定义估计量的估计误差为
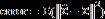
样本协方差矩阵S 的条件数偏大，也就是说S特征值的最大值和最小值距离太远，需要压缩来降低条件数。一种简便的线性压缩方法是给S加上一个目标矩阵T，目标矩阵的选取有很多种（Schafer 2005），以单位阵I为例，线性压缩（LS，Linear Shrinkage）估计量可以表示成：
线性压缩估计即是要在所有可能的线性组合中，找到一个估计误差最小的，即求解
可显式求得这个问题的解为
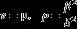
其中μ等于Σ 特征值的平均值，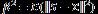
表示样本协方差矩阵的估计误差，
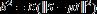度量的是样本协方差矩阵特征值分布的离散程度。Σ 的真实值不知道，
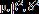也就无法计算，不过在一定的理论假设下，Ledoit(2004)构建了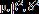的样本统计量，保证在
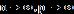时，对应的样本压缩估计量收敛于
。
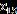样本协方差矩阵是（1）式的一个特例（ρ=0），因此LS估计量的估计误差小于等于样本协方差（n,p足够大的时候），误差减小的幅度取决于两个数值p/n 和 ρ，值越大，估计误差减小幅度越明显。LS估计量不依赖于随机变量的分布，而且中间过程涉及的变量都可以显式计算，因此计算效率非常之高，全市场3000只股票计算一次协方差矩阵耗时在毫秒级别，因此也是我们之前研究中最常用的协方差矩阵估计方法。Python（sklearn. covariance.LedoitWolf）, MATLAB（作者个人主页有作者自己编写的代码可下载），R（nlshrink package）都有成熟的工具包可调用。
记S的特征值为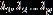
，其对应特征向量为
，则S可以谱分解为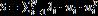
。压缩估计量可以表示成：
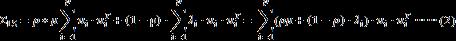
可以看到，S的特征值
被线性压缩到了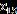的
，也就是说向真实协方差矩阵Σ 特征值的平均值
靠拢，靠拢程度取决于ρ的大小。这样
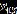特征值的分布区间相对S而言得到了一定的压缩，矩阵的条件数减小，用它做后续的组合优化，结果对数据误差的敏感性也会降低。
LS是给样本协方差矩阵S所有特征值设定了同一个目标，做全局压缩。另一种更灵活的非线性压缩（NLS, Nonlinear Shrinkage）方式由Ledoit(2017)近期提出，它的形式和(2)很类似，可以写作:
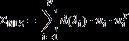
这里d(⋅) 是一个一元函数，在LS的（2）式中d(⋅)是一个一元函数。在对总体的协方差矩阵，数据产生过程和函数d(⋅)的特性做了一些理论假设后，可以证明下面oracle 函数可以最小化NLS估计量的估计误差：
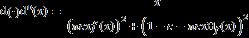
其中 c=p/n, f(⋅)是协方差矩阵特征值的极限谱分布函数,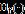 
是其对应的Hilbert变换。Ledoit(2017)通过核函方法计算得到样本协方差矩阵谱分布函数
、对应的Hilbert变换
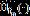和oracle函数
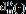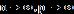，并证明当时
。
NLS和LS对样本协方差矩阵特征值的压缩效果不同。对于极大和极小的特征值，NLS和LS一样也会将其往均值方向压缩，但中间区域的特征值压缩方向有可能是远离均值的，NLS会把特征值向其附近特征值取值集中的区域压缩，每个不同特征值处的压缩强度都是不一样的，是一种局部性质。Ledoit (2017)通过仿真模拟发现，在真实协方差矩阵的条件数较大、样本集中度（p/n）较小或样本数量较多时，NLS相对LS的估计误差减小幅度非常明显。而且NLS计算过程里涉及的变量也都是可以显式计算的，运算速度非常之快，和LS基本相当，因此之前采用LS估计的研究人员可以非常便捷的转移到NLS上。
需要注意的是，Ledoit(2017) 附录 C有一处小错误，其文后所附的MATLAB代码需要做几处对应的修改。
2.3 因子模型
假设市场上有p个股票，我们已经找到K个风险因子，股票 i 在因子k上的暴露度为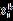
, 记p×K矩阵B为因子暴露度矩阵
，则做横截面回归
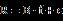
可以估算得到横截面上的风险因子纯因子收益率
。考虑到横截面上股票特质方差的差异，需要采用WLS（Weighted Least Square）以保证得到的估计量同时也是极大似然估计，权重为个股特质方差的倒数。个股特质方差和其市值平方根倒数近似成正比（参考BARRA USE4和我们之前报告的A股实证结果），所以实际计算的时候可以采用个股市值平方根作为权重。由此，股票的协方差矩阵可如下计算：
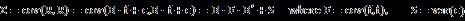
每个横截面上做一次回归得到f和ϵ的时间序列后，F和S可以在时间序列方向上进行估计。
横截面回归的Rsquared 可以用来度量风险因子对股票收益的解释程度。不过要注意的是，Rsquared的计算方式和测试股票池不一样，得到的数值会有很大差别。由于横截面回归使用了WLS方法，因此可以计算weighted rsquared，不过这个数值会比传统OLS里面的adjusted rsqaured高很多，例如我们参考CNE5 构建的因子模型，全市场回归得到的月度weighted rsqaured 平均超过40%，但 adjusted rsquared 只有20%左右。因子模型在大股票里的解释能力更强，如果缩减股票池，weighted rsquared 可以超过50%，adjusted rsquared 可以超过30%。在协方差矩阵估计中，adjusted rsquared 的参考意义更大，因为协方差矩阵估计过程中，各个股票的数据地位是平等的，adjusted rsquared 越大，能被风险因子解释的方差越多，因子模型的降维效果越明显。
我们在去年的专题报告《A股市场分析中》参考BARRA CNE5文档构建了一个因子风险模型，并和LS做对比，当时实证发现因子风险模型的效果不如LS。不过严格的讲，当时报告里的实证方法不公平，因子模型采用的是月频的风险因子数据，LS模型用的则是日频收益率数据，为保证公平性，报告后文的实证中，风险因子数据都是采用日频更新，因子收益率也是每日计算。
在上述标准模型基础上，我们用非线性压缩方法来估计因子收益率协方差矩阵F和特质方差矩阵S，以降低样本协方差矩阵条件数过大的问题， CNE5中对特质方差矩阵的Bayesian Shrinkage是一种线性压缩估计方法，采用非线性压缩有可能进一步提升模型表现。另外我们给F和S也加上了一个EWMA架构，通过调整衰减系数来调节模型对近期数据的敏感性。
2.4 多元GARCH类模型
压缩估计和标准的因子模型相对样本协方差矩阵的改进都属于横截面方向上的，也就是说它们都基于股票收益率在时间序列方向上是独立同分布的假设，不过股票在时间序列上的异质性明显，可以考虑从这个方向上改进风险模型。在一维情形下，我们可以用GARCH类模型来描述条件方差的动态变化，因此一个最直接的思路是将GARCH模型推向高维。
记t 时刻 p 个股票的收益率为 p 维向量 
，它基于t-1时刻已有市场信息
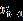的条件预期收益和协方差分别假设为
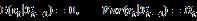。我们需要赋予
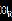一定的结构来计算极大似然函数，目前最常用的结构有两种：Engle(1995)的BEKK模型和Engle(2002)的DCC（Dynamic Conditional Correlation）模型。
BEKK模型直接对协方差矩阵建模，假设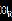满足如下递归形式：
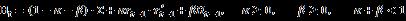
DCC则是对相关系数矩阵建模，假设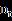
是一个p×p 对角阵, 其第i个对角线元素是股票i 在t时刻的条件方差，DCC模型假设相关系数矩阵
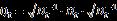满足如下形式：
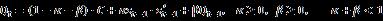
其中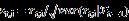
。
在满足正态分布的假设下，容易计算得到对数极大似然函数为
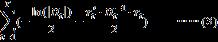
对于低维度问题，p比较小，上述极大似然函数比较好计算，R里面有成熟的package（rmgarch）可以直接调用。但如果p较大，每次求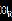的逆需要耗费
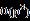运算，极大似然函数的求值将十分费时，而且后面用数值方法优化极大似然函数时，极大似然函数可能会被求值成百上千次，个人电脑上可能需要几天的时间才能算完，实用性有限。
Pakel(2017) 借鉴Lindsay(1988)提出的CL（Composite Likelihoods）思想大大降低了DCC和BEKK模型估计参数的计算量，并在一定理论假设前提下，保证估计量的一致性。这个方法分为两部，第一步是用传统样本协方差方法来估计BEKK模型里的Σ 和DCC里面的C，第二部计算CL函数，和(3)式的极大似然函数相比，它把p个随机变量两两配对，计算二维的对数极大似然函数再进行累加。这样矩阵的逆运算都是二维的，p较大时，运算速度会快很多倍。Engle(2017)对第一步的方法做了改进，采用NLS方法估计Σ和C，这样做的好处是在股票数量较多时，可以大幅降低估计误差。
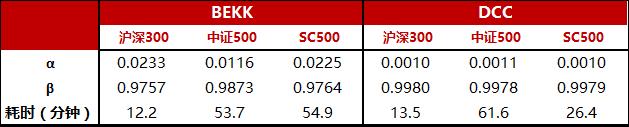
我们用Engle(2017)的方法编写python代码在A股进行了测试，时间点是2009.01.04，用过去一年的日频收益率数据分别在沪深300成份股（HS300）、中证500成份股（ZZ500）和小市值500（SC500, 中证800之后市值最大的500只股票）进行了参数估计，结果如图1所示。BEKK模型的alpha参数大概0.02附近，beta参数在0.98附近，这个和Pakel(2017)的在标普500里面的参数估计结果很接近，他们估算得到alpha大概在0.03附近，beta 在0.96附近。DCC模型估计得到的alpha和美股相差较大：A股估计得到的数值大概在0.001左右，而美股大概在0.007，也就是说A股股票间的条件相关系数矩阵对新收益率数据不敏感，动态性不强；造成这种结果的一种可能性是A股股票间的相关系数确实变化不大（这个与主观感觉有出入），另一种可能性是DCC模型设定不适合A股，存在模型设定偏误。 DCC模型的beta在美股和A股都在0.99左右，比较接近。
图1：用CL方法估计得到的BEKK 和 DCC模型参数 |
资料来源：东方证券研究所 & Wind 资讯 |
模型参数估计耗费的时间值得关注。在个人电脑上（i5-4590+16G内存+pycharm+ python3.5），估算沪深300成份股300只股票的DCC和BEKK模型参数，只需10分钟左右，但增加到500只股票（ZZ500&SC500）时，耗时接近一个小时。CL方法和最初的MLE估计方法几天的耗时相比已经大幅降低了，而且在实际实盘投资中也可用，开盘前运行一次，输入到组合优化中得到组合权重即可。不过对于长时间的历史回溯而言，累加起来的耗时量非常惊人，调参数困难。程序耗时的原因可能和代码编写有关系，计算CL函数时需要通过BEKK和DCC的迭代式反复循环计算，而后续在优化CL函数时，CL函数可能会被反复求值上千次，总运算量巨大。虽然迭代式的代码我们已经用Cython进行了加速，但目前看来效果并不理想，用纯C语言来写可能效果会更佳。
鉴于DCC和BEKK模型的耗时，我们可以考虑采用DCC模型的一个简化版本CCC GARCH，它假设DCC模型中的条件相关系数矩阵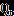
是一个常数矩阵，不随时间变化，条件协方差的变化完全由个股条件方差的变化引起。这样估计参数时，只需要对每个股票做时间序列上的一维GARCH模型拟合，然后计算devolatised return的相关系数矩阵即可，计算量大幅降低。图1在A股估计得到的DCC模型alpha很小，在时间序列上的动态性不强，支持我们采用CCC GARCH模型做简化。Pakel(2017)做过大量Monte-Carlo仿真测试，结果显示当股票数量较少时（100只左右），DCC相对CCC模型的估计误差降幅明显，但随着股票数量的逐步增加（1000只），误差的相对降幅越来越小；而且如果用真实的股票收益率数据构建全局最小方差组合（GMVP），两者的结果基本相当。
最后补充一点，Pakel(2017)和Engle(2017)在做实证时都是选取历史上一直都在正常交易的股票作为标的，但A股实际投资中，不可避免会碰到很多历史长期停牌的股票，我们研究发现缺失数据的填补方式对模型的使用效果影响较大。
3
实证结果
3.1 协方差矩阵估计量的评价方法
协方差矩阵数值不可以通过现实数据观测得到，需要设计一定的方法去检验。实证中用的最多的方法有两种。一种是Monte Carlo 模拟，预先设定协方差矩阵数值，按照一定的概率分布去随机模拟生成一系列样本点；基于这些样本点，再用不同的方法去估计得到协方差矩阵，看看哪种方法得到的估计值距离预先设定的数值最近。距离的定义方式有很多，上文2.2节介绍的Frobenius距离是一种，其它可以参考使用的还有Lediot(2017b)、Liu(2007)。
需要注意的是，用距离方法判断协方差矩阵估计量好坏的前提是必须知道真实协方差矩阵数值，所以适宜配合MonteCarlo模拟方法使用。股票数量较多时，不能拿样本外收益率的样本协方差矩阵作为真实协方差矩阵的替代值。如果股票数量p较小，收益率样本点数量n较多，那么当
时，样本协方差矩阵是真实协方差矩阵的一致估计量，估计误差会趋于零，样本足够多时，可以拿样本协方差矩阵作为真实协方差矩阵的近似值。但如果股票数量较多，甚至是组合优化里经常碰到的p>n的情形，我们则需要考虑同时
时样本协方差矩阵的一致性，但此时一致性在绝大多数情况下都不成立（Ledoit 2004, Theorem 3.1），也就是说估计误差不趋向于零。所以，一个估计量距离样本协方差矩阵很近，并不代表它距离真实协方差矩阵近，事实上，当p/n较大时，压缩估计量都可以相对样本协方差矩阵大幅降低估计误差，距离真实协方差矩阵更近。
另一种评价方法则是实用主义的。在组合优化领域，通常的方法是用不同协方差矩阵估计量构建全局最小方差组合（GMVP, Global Minimum Variance Portfolio），看哪种方法得到的GMVP组合的真实方差最小。GMVP的收益率序列是一维的，样本方差是真实方差的一致估计量，因此样本数量较多时（例如：五年的日收益率），可以用样本方差作为真实方差的近似值。GMVP组合通过下列组合优化问题得到：
下文用A股数据比较了五种协方差矩阵估计方法的效果，包括：
1）因子模型（FM）。在标准因子模型基准上，用非线性压缩方法估计因子收益率协方差
矩阵和特质方差矩阵， 并加上EWMA时变结构。
2）线性压缩模型（LS）。压缩目标选择我们之前报告里一直用的平均相关系数矩阵。
3）非线性压缩（NLS）。参考第2.2节
4）CCC GARCH.
5）FM+CCC：把FM和CCC模型估计得到的协方差矩阵进行简单平均，这样可以一定程度
上降低模型设定偏误的影响，一些实证研究发现这种多模型组合的方式能获得比单模型
更好的效果，例如Caldeira(2017).
3.2 月频 GMVP
历史回溯测试的实证区间设定为2009.01.4 – 2017.10.31，每个月初，我们基于过去一年的日收益率数据，用不同的协方差矩阵估计方法，分别在沪深300成份股（HS300） 、中证500成份股（ZZ500）和小市值500（SC500，中证800之后市值最大的500只股票）里面构建GMVP，持仓一个月到下个月初，滚动操作，看看不同估计方法得到的GMVP合方差的相对大小。图2报告的是这些组合的年化波动率数据。
图2：不同估计方法得到的月频GMVP年化波动率 |
资料来源：东方证券研究所 & Wind 资讯 |
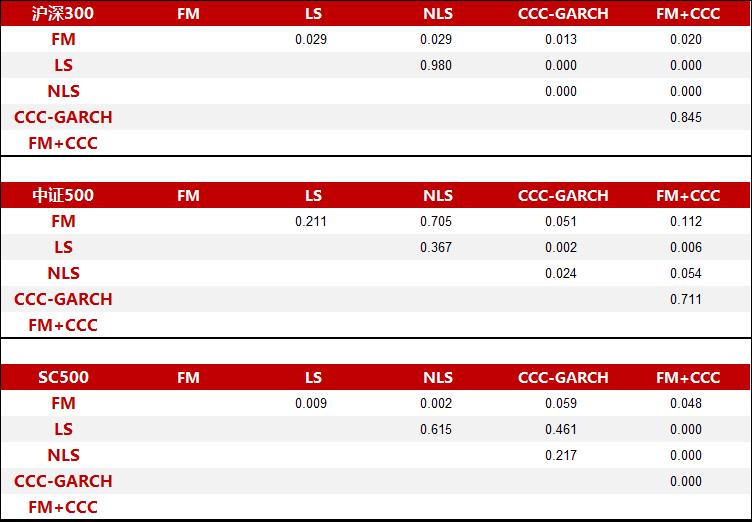
比较两个GMVP日收益率序列是否方差相等，我们采用Fligner-Killeen检验，和传统的F检验相比，它不依赖于收益率正态分布假设，对尖峰厚尾、有异常值的数据比较稳健，两两比较检验的p值如图3所示。如果投资者想检验月频收益率的方差，样本数量比较小，也可以考虑采用Ledoit(2011)的bootstrap方法。
图3：不同估计方法得到的月频GMVP日收益率方差是否相等的Fligner-Killeen 检验p值
|
资料来源：东方证券研究所 & Wind 资讯 |
从上图可以看到，虽然NLS对样本协方差矩阵特征值的压缩方式比LS更精细，但不论在HS300、ZZ500还是SC500里面，两种方法得到的GMVP组合年化波动率数值相差非常小，而且差额在统计上不显著（5%置信度）。不过上述实证涉及的情景非常有限，实际投资中会碰到很多未知情况；而Ledoit (2017)的Monte Carlo仿真测试显示NLS相对LS在很多情形下是有明显优势的，因此我们还是建议之前使用LS估计量的投资者转到NLS上，增加的计算量负荷非常少，但或许能应对的未知情况更多。
和之前报告《A股市场风险分析》的结论相反，图2里面因子模型FM表现在三个成份股里面都要好于LS，而且在沪深300和SC500里面统计显著，原因是因为我们对之前的因子模型做了三点改进：①采用日频数据，②因子收益率协方差矩阵和特质方差矩阵用NLS估计, ③因子收益率协方差矩阵和特质方差矩阵增加了EWMA的时变特性。其中第三点是最重要的。如果不加入EWMA架构,因子模型在沪深300内GMVP组合的年化波动率等于17.9%, 和LS,NLS模型非常接近，差异统计上不显著。也就是说，如果不考虑时间序列方向上的改进，横截面上日频因子模型FM、线性压缩LS和非线性压缩NLS没有显著差别，投资者可以任选其一，从计算效率上讲后两者更好。
CCC-GARCH和FM互有胜负，沪深300内CCC-GARCH比FM好，且差异在统计上显著；SC500内FM比CCC-GARCH好，且差异在统计上显著。如果把两者等权合在一起（FM+CCC），会发现其GMVP波动率数值在不同成份股内都是最小，虽然有时候这种数值差异在统计上不显著。
总结来说，横截面上改进风险模型效果不明显，时间序列方向上的改进更显著。加入了时变结构的因子风险模型表现已经很好，但并不能保证最好，和CCC-GARCH这样的纯统计模型结合在一起可以进一步提升模型表现。
3.3 周频 GMVP
月频调仓是量化实证研究中最常用的调仓频率，但实际投资中提高调仓频率一般会更有益处，一方面IC衰减速度较快的技术类因子有效时，提高调仓频率可以减小IC衰减的影响（参考前期报告《在alpha衰退之前》）；另一方面即使技术类因子失效，提高调仓频率增加不了alpha，每一次调仓都是在做一次风险控制调整，提高调仓频率有助于降低跟踪误差和风险暴露，从而提升信息比。投资者需要做的是在高频率调仓中控制每次调仓的换手率，保证总的换手率不要增加太多。因此需要测试一下高频调仓下不同风险模型的效果。以下测试了周频的情况，其它回溯测试设置同上。
图4：不同估计方法得到的周频GMVP年化波动率 |
资料来源：东方证券研究所 & Wind 资讯 |
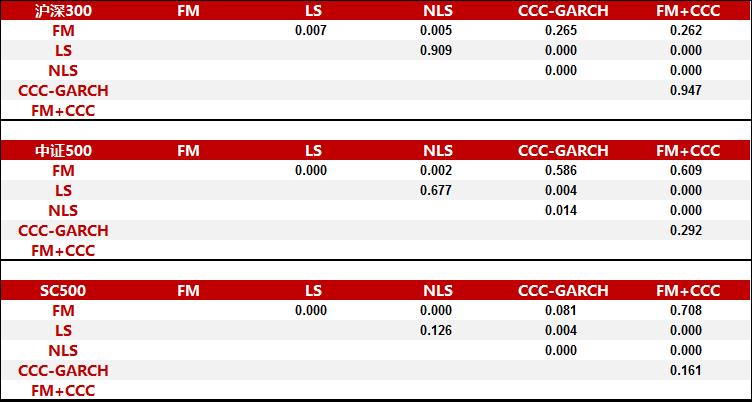
图5：不同估计方法得到的周频GMVP日收益率方差是否相等的Fligner-Killeen 检验p值 |
资料来源：东方证券研究所 & Wind 资讯 |
不同模型之间对比来看（图4，图5），和之前月频结果比较类似。加了时变结构的FM和CCC_GARCH要比纯横截面改进的LS和NLS模型要好，把FM和CCC_GARCH组合在一起得到GMVP组合波动率数值更小，但和单个模型的差异在统计上不显著。
以上的周频组合仍是用过去一年的日频数据来估算协方差矩阵。对于高频调仓组合，可以考虑增加近期数据的权重以增加模型对市场短期变化的敏感性。图6尝试了用过去半年的数据估算协方差矩阵做周频GMVP，结果和图4非常接近。提高近期数据权重的同时也在减少样本数量，使p/n数值变大，进而增加估计误差，抵消了模型敏感度增加的好处。
图6：不同估计方法得到的周频GMVP年化波动率（用过去滚动半年的数据） |
资料来源：东方证券研究所 & Wind 资讯 |
3.4 带权重约束的月频GMVP
GMVP组合波动率的大小可以理论上反映不同协方差矩阵估计模型控制风险能力的最大值，但如果仔细看GMVP组合的权重分布，会发现很多股票被做空，个别股票的权重异常高（例如：超过20%），和真实的投资限制差别较大。可以进一步加入约束条件，考察风险模型在实际投资中的效果。下文只以沪深300成份股为例，在标准GMVP基础上，要求股票不能做空，单个股票权重不能超过5%，这样得到的GMVP组合表现如图7所示。
图7：不同估计方法得到的沪深300月频GMVP表现 |
资料来源：东方证券研究所 & Wind 资讯 |
和图2相比，增加的约束条件限制了风险模型调节风险的能力，所以得到的GMVP波动率都比无约束条件下的高。不同模型间，从波动率数值上看，还是FM和CCC-GARCH要比LS和NLS好，但此时数值的差别在统计上不是很显著；把FM和CCC-GARCH组合在一起可以进一步降低GMVP的波动率，而且它相对LS和NLS模型的优势在统计上更加显著。
在时间序列方向上改进波动率模型是有代价的，可以看到FM和CCC-GARCH的GMVP换手率明显要比LS和NLS高，把FM和CCC-GARCH组合在一起可以降低部分换手率。真实投资中，我们除了单个股票权重限制，可能还会加上跟踪误差、风险因子主动暴露等约束，限制更严，用时变风险模型实际增加的换手率会比上面测试结果低，但对应的，时变风险模型降风险的幅度也会减小。究竟是时变模型带来风险下降的利好多，还是换手率增加带来的损失多，取决于alpha模型、组合约束条件、产品规模、交易成本等因素，不同的问题可能会有不同的结论，但至少这是一个值得尝试的改进方向，特别是那些交易便利的私募、券商自营等机构。
4
总结
协方差矩阵估计领域的研究成果众多，不可能一一比较，从已读文献里的仿真和实证结果看，非线性压缩NLS应该是这个领域一个比较领先的方法，但报告实证发现在实际投资中它和我们之前用的简单线性压缩LS、标准化因子模型（不加时变结构）效果没有显著差别。因此个人感觉，如果假设股票收益率在时间序列上是独立同分布，纯靠横截面方法去改进风险模型，空间可能不大。给风险模型加上时间序列结构可以增强模型的风险控制能力，FM和CCC-GARCH的实证结果说明了这一点，但改进的代价是会增加换手率。把不同的时变模型组合在一起可以进一步加强风险模型的控风险能力，并降低换手率。报告实证用的是FM+CCC组合，除此之外BEKK和DCC-GARCH也是可以考虑纳入，但程序代码上可能还要再做进一步优化。
联系人
朱剑涛 021-63325888*6077
王星星 021-63325888*6108
张惠澍 021-63325888*6123
邱蕊 021-63325888*5091
李晓辉 021-63325888*1585
田钟泽 021-63325888*1589
罗鑫明 021-63325888*1588
王冬黎 021-63325888*1590
期待与您的交流！
以上是关于风险模型在时间序列上的改进 ——《系列之三十一》的主要内容，如果未能解决你的问题，请参考以下文章
Qt系列文章之三十一 (基于QThread互斥量的线程同步线程)
YOLOv5v7改进之三十二：引入SKAttention注意力机制