时间序列模型讲座回顾

Posted 2021-05-02 XJTLU数学建模

本期主题：时间序列模型讲座回顾

2017年11月刊18

时间序列模型属于计量经济学范畴，对数学要求不高。

（我仿佛听见了你们的欢呼声？？？）

时间序列模型一般分为两种：平稳时间序列和非平稳时间序列

平稳时间序列：均值、方差都是常数

非平稳时间序列：均值、方差在变

一、时间序列成分

趋势、循环、季节、不规则

1.趋势成分

在一段较长的时间内，时间序列往往呈现逐渐增加或减少的总体趋势。时间序列逐渐转变的性态称为时间序列的趋势。

长期影响因素→时间序列的长期动向→趋势成分

2.循环成分

时间序列常常呈现环绕趋势线上、下的波动。

任何时间间隔超过一年的，环绕趋势线上、下波动都可归结为时间序列的循环成分。

围绕长期趋势线的上下波动→循环成分

3.季节成分

季节因素引起的一年内有规则的运动→季节成分

拓展：季节成分也可用来描述任何持续时间小于一年的、有规则的、重复的运动。

例如：一天内某路口的交通流量

4.不规则成分

时间序列的不规则成分是剩余的因素，它用来说明在分离了趋势、循环、季节成分，时间序列值的偏差。

短期的，不可预期和不重复出现的因素引起的随机波动→不规则成分

Tips

时间序列模型中，首先依次分离出趋势、循环和季节成分，剩下的都归为不规则成分（残差），并对其进行检验，检验残差是否与前面三个成分相关，检验均值与方差是否为常数。

二、平滑法预测

移动平均法，加权移动平均法，指数平滑法

目的：“消除”不规则成分所引起的随机波动。

优点：平滑方法很容易使用，而且对近距离的预测，如下一个时期的预测，可提供较高的精度水平。预测方法之一的指数平滑法对资料有最低的要求。

缺点：平滑方法对稳定的时间序列——即没有明显的趋势、循环和季节影响的时间序列——是合适的，这时平滑方法很适应时间序列的水平变化。但当有明显的趋势、循环和季节变差时，平滑方法将不能很好地起作用。

1.移动平均法

计算移动平均数时每个观测值权数权数相同。

公式：移动平均数=最近n期数据之和/n

波动大，n取大；波动小，n取小。

2.加权移动平均法

对每期数据值选择不同的权数，然后计算最近n个时期数值的加权平均数作为预测值。

通常，最近时期的观测值应取得最大的权数，而比较远的时期权数应依次递减。

3.指数平滑法（属于加权移动平均法）

只选择一个权数（最近时期观测值的权数），其他时期数据值的权数可以自动推算出来。当观测值离预测时期越久远时，权数变得越小。

模型：Ft+1=αYt +（1-α）Ft

    式中Ft+1——t+1期时间序列的预测值；

        Yt——t期时间序列的实际值；

        Ft——t期时间序列的预测值；

        α——平滑常数（0≤α≤1）。α越大，Yt可信度高，噪音小

指数平滑法的特点：

指数平滑法提供的预测值是以前所有预测值的加权平均数，但所有过去资料未必都需要保留，以用来计算下一个时期的预测值。

一旦选定平滑常数α，只需要二项的信息就可计算预测值。

根据（11-2），对给定的α，我们只要知道t期时间序列的实际值和预测值，即Yt和Ft，就可计算t+1期的预测值。

对指数平滑法感兴趣的同学可以自行百度“卡尔曼滤波”～

三、利用趋势法推测

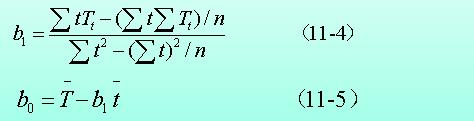
公式格式错误只能截图了…

四、利用趋势和季节成分进行预测

模型：

Yt =T×S×I

上式中：Yt--时间序列的数值

        T --趋势成分

        S --季节成分

        I --不规则成分

1.季节指数计算

（1）计算中心化移动平均数（取四个数的平均数，然后再取两个数的平均数）

（2）计算季节不规则值（原始值／中心化的移动平均数=季节不规则值）

（3）计算季节指数（季节不规则成分的数值的平均数）

2.消除时间序列的季节影响

销售量／季节指数=去掉了季节影响的值

3.利用消除季节影响的时间序列确定趋势（最小二乘法拟合）

基本模型与趋势法预测一样

4.季节调整

5.基于月度资料的模型（联系现实进行改变）

总结

Summary

​

相比之前几次讲座而言，这次讲座可以说算是比较通俗易懂了（笑）。

希望这篇推文能让大家对时间序列模型有更多的了解，给大家在寒冷的冬（秋）日（天）带来温暖～

想了解更多关于建模的知识？