时间序列分析导读(文末有福利！)

Posted 2021-05-02 通联数据Datayes

时间序列分析，是《高级计量经济学》的工具。也是我们做实证分析说必须掌握的技能。它和大家看到的统计报告和分析是不同的，大家看到的传统统计分析只是描述性的，而计量经济学的时间序列模型，具备很强的归纳能力和分析能力。简单的说前者只是马后炮的叙说，而且叙说经常会有偏差。而后者是用来做预测的。 

我在过去的帖子写到过，看未来的方法和看过去的是不同的，过去是确定性的，是无数可能中最终发生的那个，未来是不确定的，在没发生之前我们并不知道是什么。所以为了预测未来，我们必须尽可能全面的描述过去的环境，然后不断试错找寻未来最优的路径。

公平赌博

很多投资的‘’老前辈‘’会告诉你一件事：他们会有一套非常牛B的方法去预测股票市场，然后10年10倍。这显然是不可能的。因为如果一个方法真的有效，那么所有的人都会模仿那个方法，直到他的超额收益完全散失为止。所以我们在长期的市场中，既看不到专家，也看不到股神，只能看到随时都在变化的‘’投资新秀‘’。

比如04年到07年，那个技术分析横行的年代，最成功的投资者是但斌。在他写了《时间的玫瑰》之后，他的方法就彻底失效了。

市场在短时间内会抽风，但是长期内相对有效。什么叫公平赌博？我举个例子！

我拿100块的本金，去玩一个丢硬币的游戏。如果是正面，那你可以赢5块钱，是反面，你就输5块钱。

那么我们来模拟这个游戏：

第一次丢硬币：

本金100      预期收益5*50%-5*50%      期末资产预期100 

结果：反面      期末资产：95 

第二次丢硬币：

本金95      预期收益5*50%-5*50%      期末资产预期95 

结果：反面      期末资产：90 

那么，第三次资产期末的预期是多少？是本金100？不是。是第二次的资产95？也不是。第三次赌博前，你剩下的本金是90。

这个过程就叫做鞅，即：未来的期望和过去的条件没有关系，只和当下有关。 

就好比在丢硬币的游戏中，某人赢了10次，那么下一次赢钱的概率不会因为他过去赢了10次而提高。 

过去的一个世纪中，西方经济学家都有一个偏执的想法，即市场可以消化所有信息（经济学的假设，一般都是所有人都是聪明人，和某些网红所有人都是笨蛋的假设不一样。）因此在人们对当前所有信息的认识下，金融市场就会在各资产间套利，一直到所有的资产预期收益率都相等为止。 

即：在当前信息下，未来价格的期望现值=当前的价格（又是贴现定价。现金流贴现模型不熟悉的继续强化） 

市场的波动，是由于信息的改变导致的。我举个例子，比如15年1到2月，信息准则下石油价格会继续下跌，所以石油公司的股票价格持续的下跌。之后石油价格逆转，石油价格是石油公司利润的来源，一旦逆转，石油公司的未来预期现金流就会增加，这时候金融市场就会快速套利，从巴菲特买石油公司到现在的价格，其实就用了半个月的时间。当然在巴菲特抄底石油公司之前，很多石油高手都被套了。 

再比如14年的银行暴涨，市场对利率的预期产生了偏差，即：在14年年初，一直认为去杠杆调结构是重中之重，但当14年连续双降之后，银行股票马上暴涨，这个过程也只用了1个月的时间。 

西方学者认为，股票市场会摆动的原因就是因为信息发生改变，所以股票价格会上下波动。因为市场每时每刻都要在信息下给金融资产定价，而且价格只和当前信息有关和过去信息无关。 

很多人把信息发生改变导致股票价格暴涨理解为市场无效，因为过去恐惧，这和理论是有明显的偏差的。我们看到的暴涨，是一种套利的行为。反而是趋向于均衡的过程。换句话说，信息不变，股票价格就不可能暴涨，不管PE还PB什么的。 

平稳性

平稳性检验是为了证实股票价格是否是公平赌博的第一步。如果是公平赌博，那么他的收益期望和赔率都应该是可测的。 

大家看，在丢硬币的游戏中我们可以预测丢硬币的赔率和期望。所以如果能给金融资产定价，一样可以预测他的期望和赔率。这就要求，波动在一定的范围之内，而且任何一段时间的方差都应该是一致的。（PE虽然波动也是在一定的范围内，但是任何时间段上的方差不是一致的，所以他不是平稳序列，是一个变方差的布朗运动。）

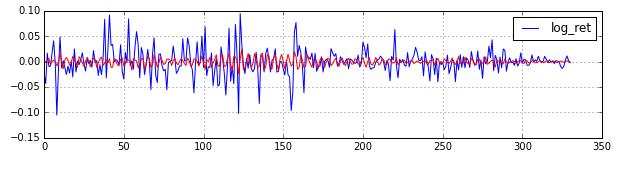
如果是平稳的，我们就能够认为他在形式上是一个公平赌博的形式。当然对数收益率，一般都是平稳的。

自相关性和偏自相关性

自相关性检验和偏自相关性检验是杜绝‘’骰子英雄‘’最好的办法。它是检验过去的信息是否影响未来收益率的最有效办法。 

什么叫自相关性呢？ 

所谓自相关性就是，过去的收益率和明天收益率的关系。如果等于0，就是无关，如果大于0，未来的收益率就可以被过去的收益率表达。其实这个检验同时针对了技术分析流派和PE流派。 

即如果自相关性大于0，那么股票价格可以用过去的收益率或者形态预测，应为利润和价格一般有协整关系，或者说是可以用过去利润的变化率来预测。但是如果等于0，就是说，一切的过去形态和未来收益率无关，利润趋势也和未来的趋势无关。我们不可能从图形和形态上去预测未来。 

而检验的结果通常是这样的：

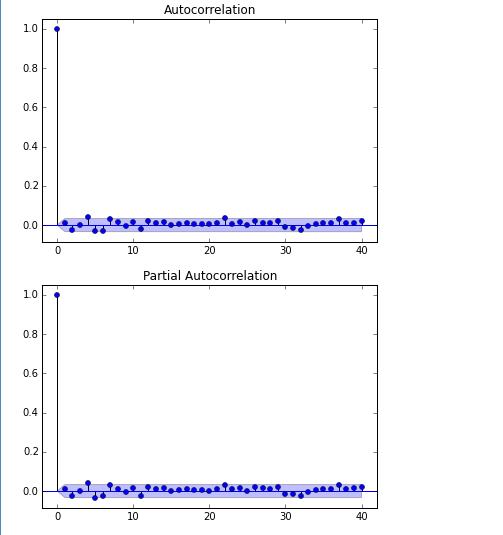
每个单位数字表示滞后多少阶。这个不难理解，用日收益率做个比方，所谓1阶自相关性就是，昨天的收益率和今天的收益率的关系，2阶代表，前天的收益率和今天的关系，以此类推。

而自相关检验中，有一个名词叫截尾。所谓截尾的意思是，在某一阶（M）后，自相关性超过蓝色区域（两倍标准差）的概率小于0.05%。这时候我们认为他是M阶自相关，也叫做M阶截尾。但我们看上图，基本上所有阶的自相关系数都在蓝色2倍标准差之内。这说明，该序列没有自相关性，也就是过去的收益率、价格、利润形态等和未来的收益率没有任何关系。

而这实际上就是股票市场的特点，也是有效市场假说被认可的原因。（技术分析被边缘化的真正原因即是这个检验。而不是其他莫名其妙的理由）

自回归移动平均模型(ARMA模型)

这个模型我不打算多讲，因为涉及到很多统计学和数学的知识，大家只要明白，他是用过去的信息来预测未来的模型即可。（本人有方便到家的一键ARMA模型python版，只要输入那只股票，从什么时候开始，就可以自动建模。） 我们看对于可预测的： 它会是这样的

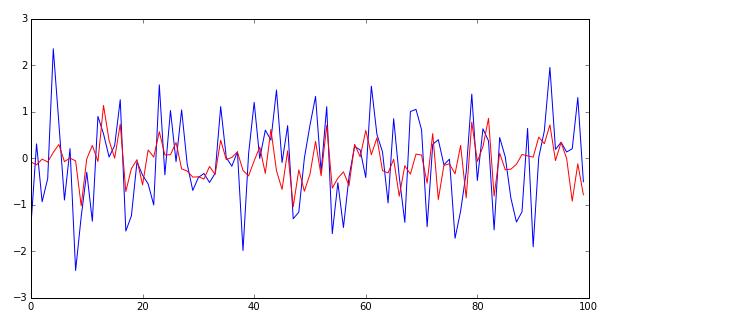
对于不可预测的，就好比这些收益率，就是这样的：

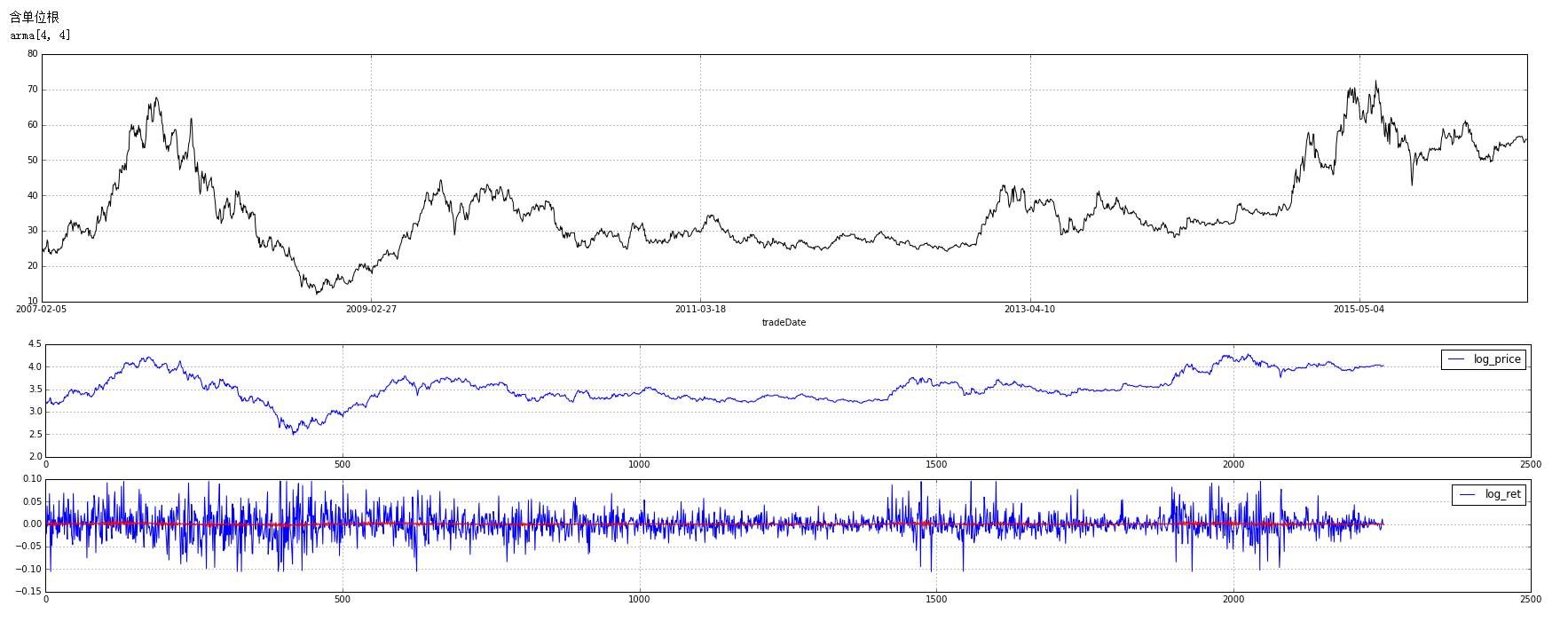
它就是一条基本水平的直线，这说明趋势不可预测。

arch性检验

当然事情总是不那么绝对，很快人们就发现自回归移动平均模型在假设上的一些缺陷。比如它实际上会有“波动率聚集”（volatility clustering）的现象，即所谓的厚尾效应。当一个大的扰动产生的时候，会有一个相对较大的扰动产生，这种扰动可能是正的也可能是负的。比如当人们看到一只股票暴涨的时候，它可能会继续暴涨，或者直接暴跌。同理如果买了一只暴跌的股票，它会持续的暴跌或者强力反弹。暴涨暴跌并不确定，但是标准差却能确定。（所以抄底很危险，不是抄到金子就是挖到地雷，在抄底前一定要想清楚能不能因为价格暴跌而拿上10年，并且一定不能放杠杆。再次看出巴菲特这种赌术高手和普通小散之间的区别）

什么叫ARCH性？一个直观的例子就是先建立一个均值模型，然后减去趋势剩下扰动，再对扰动进行自相关性检验。 

其结果：

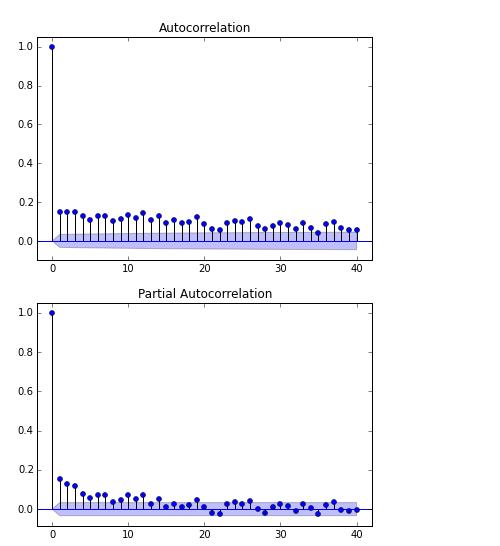
这是万科A的20年股票价格ARCH性检验。我们可以看到扰动有很强的自相关性。这说明，当出现一个很大的涨幅的时候，通常又会出现一个还是很大的涨幅或者跌幅。这种扰动，我们称作条件异方差，它意味着在一个很大的方差的条件下，下一个方差也会很大。大量的文献表明，这样的扰动是由贪婪和恐惧引起的。而且如果玩期权的同学会发现，当股票市场暴跌之后会出现高贴水，这就是由于条件异方差引起的，并不是什么市场给的套利机会。因为短期的方差增加，长期的方差平缓，所以出现了贴水。（条件异方差导致隐含波动率上升）

广义自回归条件异方差模型(garch)

该模型具体也不讲，本人也做了傻瓜一键版。但是大家得知道模型表达的是什么意思。

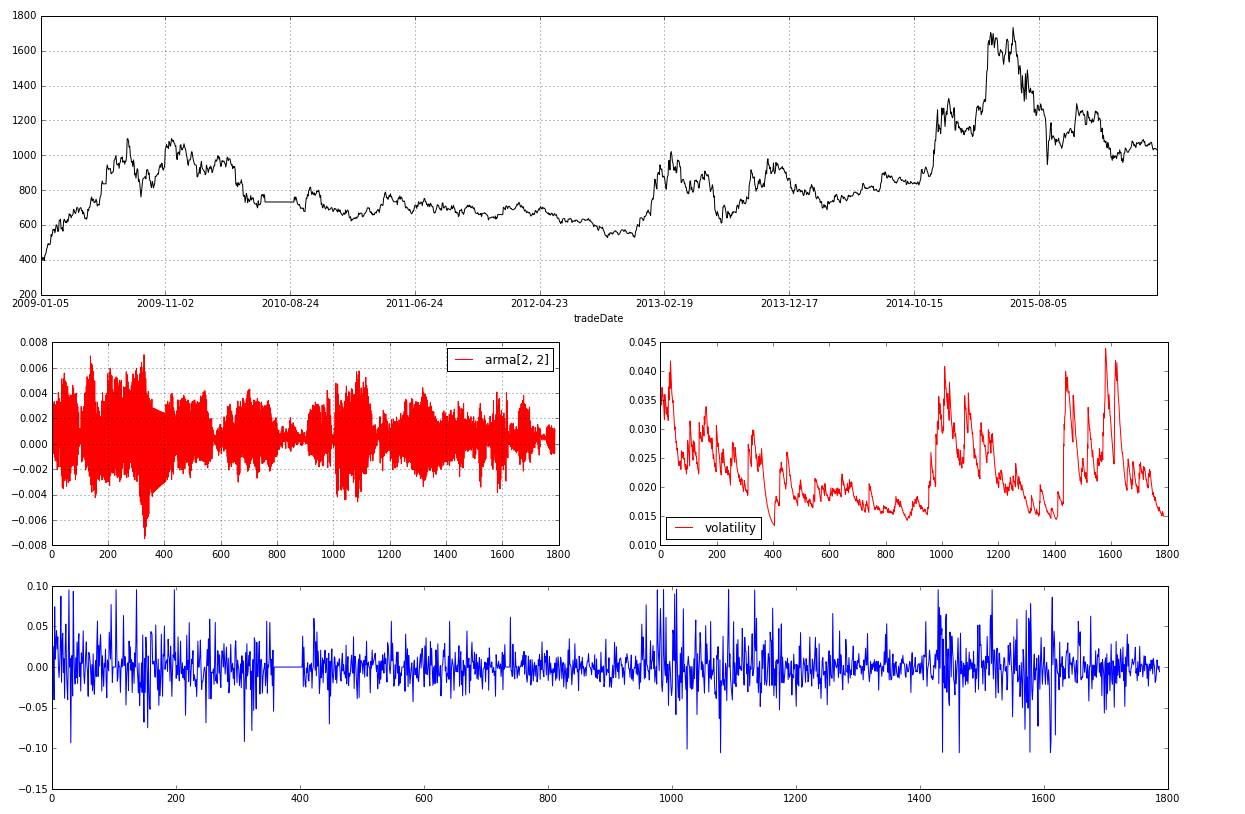
大家看到，右边红色的就是garch（1，1）模型的波动率，它可以很好的刻画暴涨和暴跌的情况（也就是趋势性）。

和几何布朗运动相比，ARMA-GARCH模型更具预测性。几何布朗运动只是建立在acf检验上的一个简单的模拟，他不具备预测的特点。而arma和garch 则是用过去的信息去预测未来。这些模型应用非常广，如果不用这些模型预测，无论你在利润表上拿ROE或者利润做线性回归，还是在K线上做技术分析，都不可能很好的刻画出未来的趋势。其实损益表利润线性外推法和K线线性外推法是一样没撒卵用的，因为利润和价格是协整关系。当然扯到协整，就是因果检验的问题，本质上还是时间序列分析。

本文已获得原作者授权，转载须经同意

1、福利：

2、昨日获奖用户：

3、活动：

“关注支持优矿Uqer，赢儿童节好礼”(7本投资书籍)活动正在火热进行中，只要轻松3步：关注优矿雪球官方账号+转发任一优矿雪球文章+发送转发文章标题，便可参与。

点击文末"阅读原文"，快去参与获奖~

投稿及合作，请发邮件至：

[e-mail]

或：直接后台留言

回复关键字查看更多精彩内容！

回复：投研，查看《你的投研方式out了吗？》

回复：多因子投资，查看《进行多因子投资，你不得不知道的事》

回复：520，查看《代码里深藏爱，520，看程序猿GG如何表白》

回复：调仓信号，查看《微信订阅调仓信号，模拟交易调仓随时看！》

回复：阿尔法投资，查看《通联数据CEO王政做客北大|谈Alpha投资能否战胜人类》

回复：多因子调仓，查看《樊小妹教你多因子调仓嫁豪门》

点击“阅读全文”，赢儿童节好礼！