时间序列预测简单回归(Simple regression)模型
Posted 哈希大数据
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了时间序列预测简单回归(Simple regression)模型相关的知识,希望对你有一定的参考价值。

英国生物遗传学家Galton观察了1078对夫妇与子女,分析他们的身高关系。以每对夫妇的平均身高作为x,取他们的一个成年儿子的身高作为y,将结果在平面直角坐标系上绘成散点图,发现趋势近乎一条直线。计算出的回归直线方程为:Y=33.73+0.516x 这种趋势及回归方程表明父母平均身高x每增加一个单位时,其成年儿子的身高y也平均增加0.516个单位。
结果表明,虽然高个子父辈确实有生高个子儿子的趋势,但父辈身高增加一个单位,儿子身高仅增加半个单位左右。
平均说来,一群高个子父辈的儿子们的平均高度要低于他们父辈的平均高度,他们儿子的身高没有比他们更高,高个子父辈偏离其父辈平均身高的一部分被其子代拉回来了,即子代的平均身高向中心回归。
低个子父辈的儿子们虽然仍为低个子,平均身高却比他们的父辈增加了,即父辈偏离中心的部分在子代被拉回来一些。说明子代的平均身高没有比他们的父辈更低。正因为子代的身高有回到父辈平均身高的趋势,才使人类的身高在一定时间内相对稳定,没有出现父辈个子高其子女更高,父辈个子矮其子女更矮的两极分化现象。
我们接触过的变量关系可以分为两大类:
确定性关系,例如:I=U/R,S=V等;
不确定性关系,而变量之间的不确定关系又可以分为:
(1)相关关系:变量间的非确定性关系;
(2)回归关系:变量间非确定性的因果关系;
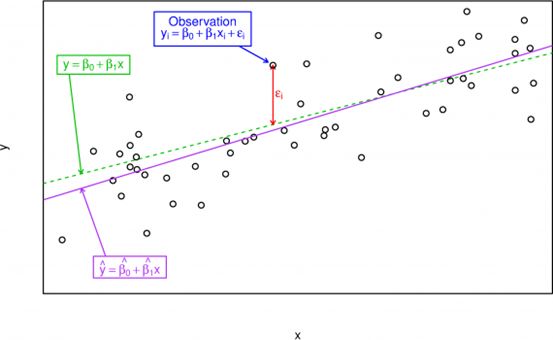
简单回归是描述回归关系的最基本的模型。简单回归模型方程:
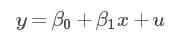
其中,y为被解释变量;x为解释变量;u为误差随机项,β0和β1为回归系数。想要从随机数据样本中得到β0和β1的可靠估计,需要对x和u的关系做一些限定,首先肯定不能相关,但相关只是度量了线性关系,u还是有可能和比如x2等项相关,对大部分回归来说这也是不能接受的。一种更好的限制方法,是对给定x时,u的期望作出假定,称之为u的均值独立(mean independent):E(u|x)=E(u),与E(u)=0相结合,就有了零条件均值假定(zero conditional mean assumption):E(u|x)=E(u)=0
最小平方估计(Least squares estimation)
我们需要根据数据,拟合模型得到模型参数 β0 和 β1 ,估测模型参数的 方法有很多,最常使用的是最小平方估计: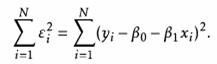
经过数学转换:
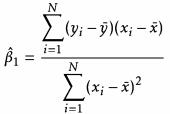
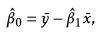
估测残差:
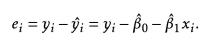
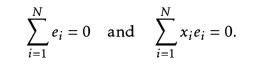
残差性质:
回归和相关关系
相关系数 r ,表示两个变量之间的相关程度, r 越大所有点越集中与一条线上。回归线的斜率可以表示为: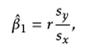
其中,sx是x观测值的标准差,sy是y观测值的标准差。
评估回归模型
1.残差图
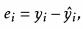
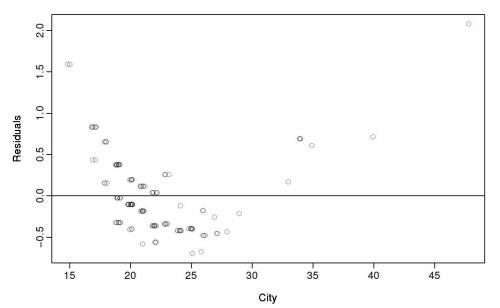

由残差图可以看出,小于20和大于30时,残差为正,在20-30之间残差为负数,因此简单的线性模型不适用于这个数据,需要非线性模型拟合这个数据。
2.异常值处理(Outliers and influential observations)
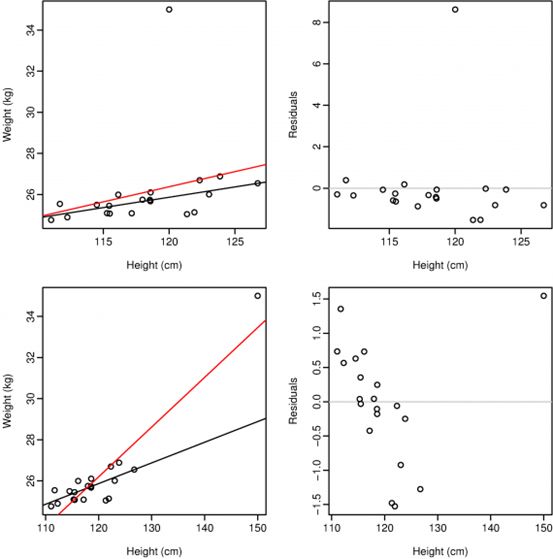
在上图中,我们使用简单的线性模型,通过将体重与身高进行回归,来预测7岁儿童的体重。所考虑的两个样本除了一个观测值是异常值外数据都是相同的。在第一排中,异常值是一个重35kg,高120cm的孩子。在第二排情节中,异常值是一个重35公斤但在150厘米处更高的孩子(在x方向上更加极端)。黑线是当每种情况下的异常值不包含在样本中时,估测的回归线。红线是包含异常值时估测的回归线。这两个异常值都对回归线有影响,但第二个影响更大,所以我们称之为有影响力的观察。残差图显示有影响的观察结果并不总是导致大的残差。
3.拟合效果评价
通常,我们评价一个回归模型拟合效果时,都会通过一个决定系数 R2 :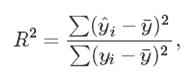
决定系数R2越大,说明模型拟合数据的效果越好。有时候我们会使用回归的残差的标准差来评价模型拟合效果:
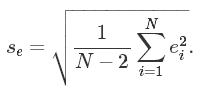
预测结果
注意预测结果不单单是一个值,应该是一个区间,即数值+置信区间的波动范围。
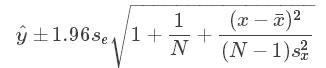
上式代表95%的置信区间的预测区间N代表样本数量,s2x代表x的标准差。
统计推断
可以使用假设检验来识别判断拟合的参数的正确性。这里使用P值来表明在原假设成立时,发生的概率。
统计学根据显著性检验方法所得到的P 值,一般以P < 0.05 为显著, P <0.01 为非常显著,其含义是样本间的差异由抽样误差所致的概率小于0.05 或0.01。实际上,P 值不能赋予数据任何重要性,只能说明某事件发生的机率。
若 X 服从正态分布和 t 分布,其分布曲线是关于纵轴对称的,故其 P 值可表示为 P = P{| X| > C} 。 计算出 P 值后,将给定的显著性水平α与 P 值比较,就可作出检验的结论 : 如果α > P 值,则在显著性水平α下拒绝原假设。如果α ≤ P 值,则在显著性水平α下接受原假设。在实践中,当α = P 值时,也即统计量的值 C 刚好等于临界值,为慎重起见,可增加样本容量,重新进行抽样检验。 具体推导公式可以查找其他资料学习。非线性拟合
线性拟合不好的情况可以用非线性拟合,适当的将变量进行数值变化之后可以用线性变化的理论来拟合非线性的问题,如选用log-log模型:
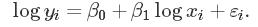
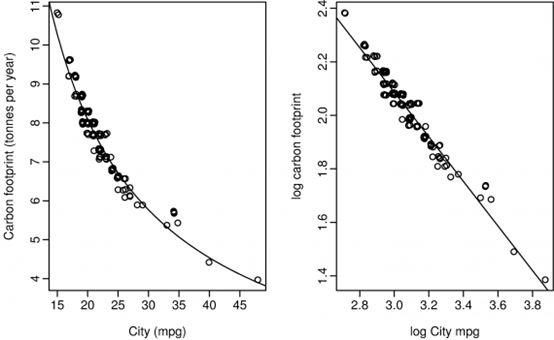
时间序列回归
我们通常会遇到时间序列数据,我们可以使用回归进行预测,我们在这里介绍一个例子:
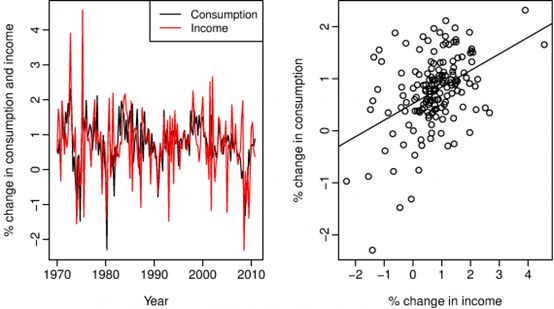

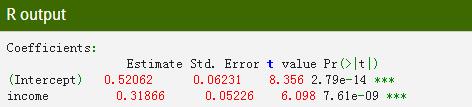
上图为美国1970年3月至2010年12月期间实际个人消费支出(C)和实际个人可支配收入(II)的季度变化百分比(增长率)的时间序列图和散点图。
估算结果如图所示,个人可支配收入增长1%将导致个人消费支出平均增长0.84%。
以上是关于时间序列预测简单回归(Simple regression)模型的主要内容,如果未能解决你的问题,请参考以下文章