时间序列预测系统
Posted AI小迷妹
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了时间序列预测系统相关的知识，希望对你有一定的参考价值。
小明是校篮球队的队长，平时需要负责制定好同学们的训练计划：晴天在室外篮球场训练，而雨天则在室内做体能训练。然而，室内训练室需要提前预定，如何提前安排好训练场地至关重要。通常，一段时间内的降雨量有一定的联系，已经有了两三周的降雨量，若是可以推测出接下来几天的降雨情况，则可以及时制定训练计划。
正如上文中所述，已知降雨量可以看成一组与时间相关的数字，也可以称作时间序列。此时，预测后续降雨量问题则可以抽象成一个时间序列预测问题，可利用回归算法实现。
图[1]中展现了序列预测系统的搭建流程，主要分为四大步骤：
1）时间序列成分分析，比如6、7月份是梅雨天气，降雨量会逐渐增加，具有一定的趋势性，而每年各个月份的降雨量都具有比较类似的规律，即为周期性；
2）预测方法选定，根据序列成分确定时间序列的类型，从而确定预测方法，比如趋势性序列可以利用自回归预测法，不存在趋势的时间序列则更适合平滑法预测，而存在周期（季节）性的序列则需要更为复杂的预测方法；
3）预测方法评估，搭建的模型存在许多未知参数，根据已知的数据计算参数，并进行误差计算，评估出最佳的预测模型参数；
4）模型预测，根据预测模型推断出后续的降雨量。
【图1：序列预测系统搭建过程】
上一篇文章中我们已经介绍了时间序列的定义：变量x(t)是一个或者一组同一统计指标的离散数据，按照发生的时间先后顺序t1,t2,…,tn排列，形成的序列集合即为时间序列。
时间序列分析的主要目的就是根据已有的历史数据对未来进行预测，比如利用历史股市价格变化预测未来股票价格，再比如上文中所述的根据历史降雨量预测未来的降雨量。
时间序列中的数据变动既存在着规律性与不规律性，序列中的每一个观察值大小是各种不同因素在同一时刻发生作用的综合结果，这些影响因素造成了序列的时间特性，主要可以下面几种类型。
趋势性：序列随着时间推移呈现一种缓慢而长期的持续上升、下降或者停留的同性质变动趋势，但变动幅度有所变化。比如，随着医疗科技水平的提高，人均寿命持续上升，再比如鸟类数目因生态环境恶化呈现逐年减少的趋势。
周期性：时间序列在一段时间内交替出现峰值与谷值的规律变化，受到诸如气候条件、生产条件、节假日或者各地风俗等因素影响。其中，最常见的是季节性的变化，比如冬夏两季用电量的增加。
随机性：时间序列中的个别数据随机波动，而整体序列变化呈现统计特性。只含有随机波动成分的序列也成为平稳序列。
趋势性与周期性都是时间序列中存在的规律性变化，单一的趋势性或者周期性序列，序列x(t)与时间t之间的关系确定，可以拟合出两者之间的函数关系。而序列的随机性体现了时间序列存在的不规律数据波动，通常情况下，这样不规则的数据波动总是存在于时间序列中的。
综合性：实际情况下，时间序列多具有两种或两种以上的波动特性。比如图[2]中展示的乘客人数统计图，每年的乘客人数存在明显的上升趋势，而每一年的人数波形类似，即存在着周期性，同时，由于序列的随机性，虽然整体统计特性存在趋势性、周期性，当个人月份的乘客人数会有随机变化。
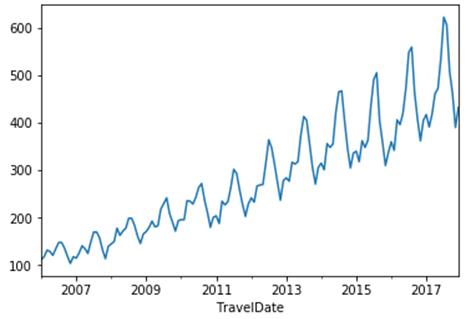
【图2：某航空公司近年乘客人数统计序列图】
平稳时间序列粗略地讲，一个时间序列，如果均值、方差没有系统的变化（无趋势），且严格消除了周期性变化，则称之为平稳序列。
验证平稳性最直观的方式是观察法，图[3]中展示的平稳序列在固定值附近随机波动，且没有明显的趋势，与图[2]中的序列波形具有明显差异，通过观察法可以区分。
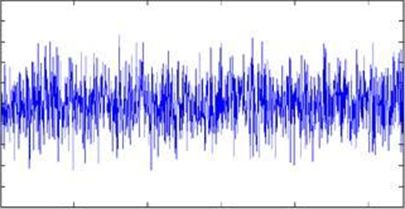
【图3：平稳序列】
然而，观察毕竟带有很大的主观性，对于比较复杂的波形，使用统计量进行验证则更为准确，其中最常用的是ADF单位根检测法。
既然ADF检验是基于自回归过程，那我们先来了解自回归（Auto-regressive，AR）模型。对于时间序列{x(t)}，若预测对象x(t)受到历史数据的影响，则可以用公式表示：
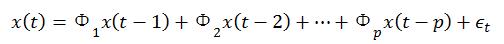
此为p阶自回归过程AR(p)。这是从线性回归发展而来，却是用{x(t)}预测{x(t)}（自己），因此称为自回归。AR(p)的特征方程为：
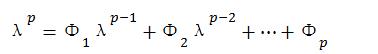
当我们通过观察或者计算分析出时间序列的变换特性后，需要根据序列的不同类型选择相应的序列预测方法。从图[4]中可以看出，综合性的时间序列通过分离出周期成分可以消除周期性，而趋势性序列则可以通过差分操作转变为平稳序列。绝大多数中短期时间序列都可以经过一定的数据操作完成平稳性处理，因此，我们将主要了解处理平稳序列的预测方法。
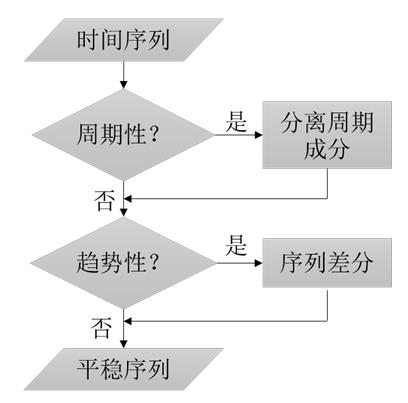
【图5：时间序列预测方法】
自回归滑动平均(Auto-Regressive and Moving Average, ARMA)模型是研究平稳随机过程的典型方法，适用于很大一类实际问题。从模型名字不难看出，ARMA模型是以AR模型与滑动平均(Moving Average, MA)模型为基础“混合”构成。
在上文中，我们已对AR模型表达式进行了介绍，了解到AR模型反映的是当前值与过去值的关系，接下来，我们先学习MA模型。MA模型反映的是当前值与当期以及过去的误差项的关系，可用公式表达为：
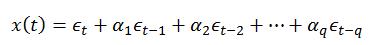
如果时间序列是它的当前和前期的随机误差项以及前期序列值的线性函数，则可将AR模型和MA模型综合，公式表达为：
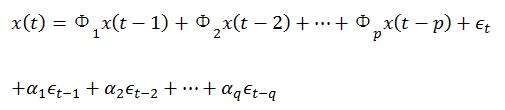则该序列为(p,q)阶ARMA模型，记为ARMA(p,q)。
当我们确定模型结构，并得出模型参数后，如何确定该方法可以较为准确地进行预测呢？我们只能根据已有的数据来对模型进行评估。所谓评估，也就是计算预测值与实际值之间的误差，误差越小，则预测模型的性能越好。
均方根误差是最常用的评估指标，其实就是计算预测值与实际值差值的均方误差的算式平方根：
利用评估准则选定模型后，则可以利用公式计算出x(t+1)的值，从而计算向后预测。值得注意的是，利用模型向前预测的时间越长，则预测误差将会越大，这是时间预测的典型特点。
想学习了解人工智能知识的小伙伴们，请关注：
以上是关于时间序列预测系统的主要内容，如果未能解决你的问题，请参考以下文章