三种方法带你玩转时间序列

Posted 2021-05-02 赢潇FM

前言

        通过移动平均法，指数平滑法和季节指数法，本文对我国餐饮业社会消费品零售总额进行了分析，预测出了本年3到5月的数据，分析过程如下。

正文

一、数据收集

本案例通过在国家统计局官方网站查询到了2014年1月到2018年1月的全国餐饮业社会消费品零售总额的月度数据，并将其导入了excel中，如图所示：

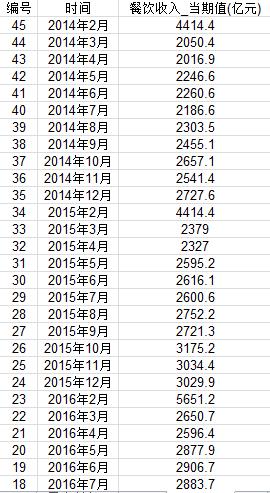
二、简单移动平均法

（一）原理

移动平均法是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。因此，当时间序列的数值由于受周期变动和随机波动的影响，起伏较大，不易显示出事件的发展趋势时，使用移动平均法可以消除这些因素的影响，显示出事件的发展方向与趋势（即趋势线），然后依趋势线分析预测序列的长期趋势。

公式如图所示：

Ft=(At-1+At-2+At-3+…+At-n)/n 　

（二）简单移动平均法缺点

1.加大移动平均法的期数（即加大n值）会使平滑波动效果更好，但会使预测值对数据实际变动更不敏感；

2.移动平均值并不能总是很好地反映出趋势。由于是平均值，预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动；

3.移动平均法要由大量的过去数据的记录。

 

（二）案例应用

由下图1可知，数据具有周期为12个月的变化，所以对数据进行12个月为间隔的简单加权平均，得到如下图2结果：

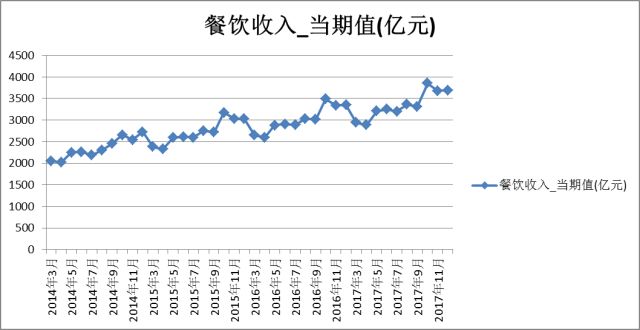
图1

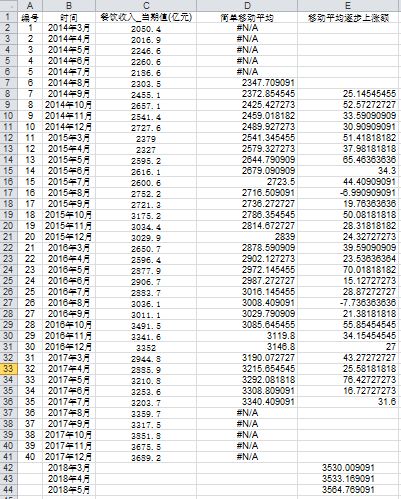
图二

最后计算进行移动平均后的全国餐饮业社会消费品零售总额逐月上涨额，因为2018年3月、4月、5月比2017年七月分别有6、7、8个月的时间差距，所以预测2018年3月、4月、5月的全国餐饮业社会消费品零售总额分别为

3530.00（3340.40+31.6*5）3533.16（3340.40+31.6*6）3564.77（3340.40+31.6*7）

 

三、指数平滑法

（一）原理

指数平滑法是移动平均法中的一种，其特点在于给过去的观测值不一样的权重，即较近期观测值的权数比较远期观测值的权数要大。根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。公式如下：

 yt+1=a*yt+(1-a)*yt式中，

•    yt+1——t+1期的预测值，即本期（t期）的平滑值St ；

•    yt——t期的实际值；

•    yt——t期的预测值，即上期的平滑值St-1 。

（二）指数平滑法的缺点：

1.对数据的转折点缺乏鉴别能力，但这一点可通过调查预测法或专家预测法加以弥补。

2.长期预测的效果较差，故多用于短期预测。

（三） 指数平滑法的优点：

1.对不同时间的数据的非等权处理较符合实际情况。

2.实用中仅需选择一个模型参数a 即可进行预测，简便易行。

3.具有适应性，也就是说预测模型能自动识别数据模式的变化而加以调整。

（四）应用案例

由下图可知，指数平滑法对实际序列具有平滑作用，权系数（平滑系数）a  越小，平滑作用越强，但对实际数据的变动反应较迟缓；

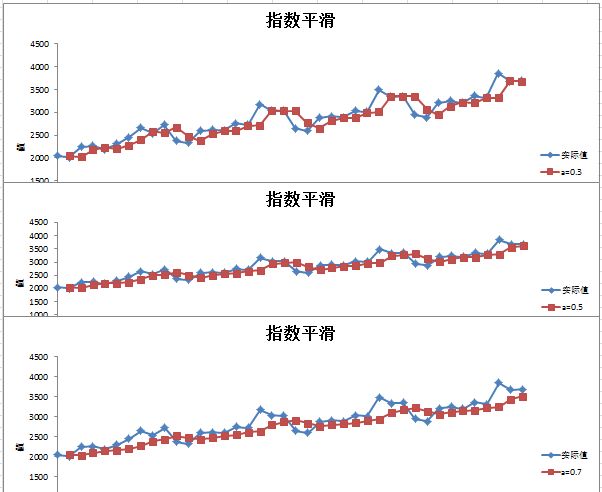
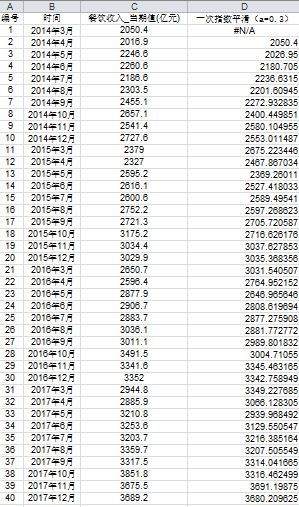
在实际序列的线性变动部分，指数平滑值序列出现一定的滞后偏差的程度随着权系数（平滑系数）a  的增大而减少，但当时间序列的变动出现直线趋势时，用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此，也需要进行修正。修正的方法也是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法，如下图：

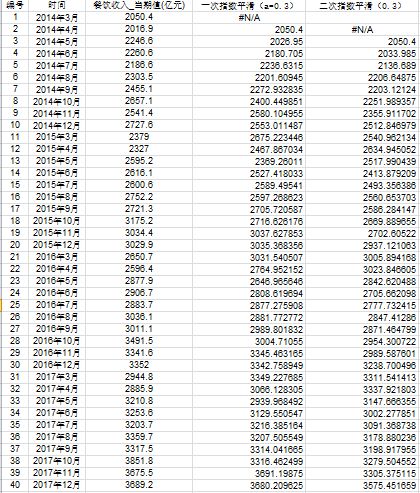
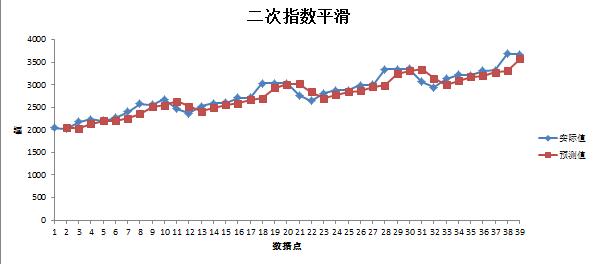
根据下图模型对未来数据进行预测：

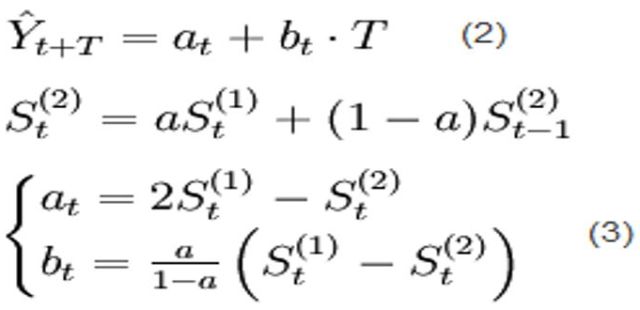
a40= 3784.96759，b40= 44.89627093，

所以2018年3月的平滑值S（2）41= 3784.96759+44.89627093*1=3829.864

2018年4月的平滑值S（2）42= 3784.96759+44.89627093*2=3874.760

2018年5月的平滑值S（2）42= 3784.96759+44.89627093*3=3919.656

 

四、季节指数法

（一）原理

简单季节指数法是指反映季节变化对销售量影响的一种简便方法。其实质就是计算各个月份的不同销售指数。

简单季节预测法的具体步骤如下：

　　1.收集历年按月份记录的历史统计资料；

　　2.计算出n年各相同月份的平均值(A)；

　　3.计算出n年每一个月份的平均值(月)；

　　4.计算季节指数，即用各月份的平均值（A）除以所有季度的平均值（B）：

　　式中：

　　SI =A/B

　　SI——季节指数。

　　5.利用季节指数(SI),对预测值进行修正：

　　Yt = (a + bT) SI

　　式中

　　SI——第i月份的季节指数(i=1,2,3,4)；

　　Yt——第t月份的销售量；

　　a——待定系数；

　　b——待定系数；

　　T——预测期月份数，

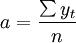
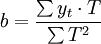
（二）案例应用

转换数据结构，并计算2014-2017年各月零售总额平均值与总的零售总额平均值，计算季节指数SI，如下图：

建立时间序列线性回归预测模型，Yt=(a+b*T)*SI，计算可得a= 2855.423，b=34.667，所以模型为Yt=(2855.423+34.667*T)*SI ，所以2018年3月-5月的餐营业社会消费品零售总额分别为（2855.423+34.667*41）*0.87771=3753.729107

（2855.423+34.667*42）*0.86031=3709.151617

（2855.423+34.667*43）*0.95699=4159.173569

点击蓝字