时间序列分析及预测的运用

Posted 2021-05-02 喜欢用数据写报告

题目：

佛罗里达州迈尔斯堡附件卡普蒂瓦岛上的Vintage饭店由Karen Payne拥有并经营，饭店刚刚经营了3年。作为一家专门海鲜的高档餐饮企业，自从Karen的饭店开业以来，她一直在为Vintage树立声誉。经过Karen及其员工的努力，她的饭店已经成为岛上最好的且营业额增长最快的饭店之一。

为了更好地规划饭店未来的发展，Karen需要建立一个系统以提前一年预测食品和饮料每个月的销售额。下表是开业前3年的食品和饮料的销售总额数据。

管理报告

对Vintage饭店的销售额数据进行分析，请为Karen准备一份报告，该报告总结了你的发现、预测和建议，包括：

1、 时间序列图。对时间序列的基本模式做出评论。

2、 数据的季节性分析。计算每个月的季节指数，并对季节性的高销售额月和低销售额月做出评论。季节指数是否有直观上的意义？请讨论。

3、 消除时间序列的季节影响。消除季节影响的时间序列是否呈现出任何趋势？

4、  利用时间序列分解法，预测第4年1-12月的销售额。

5、  利用虚拟变量回归法，预测第4年1-12月的销售额。

6、  报告的附录给出你的计算汇总表和图

假设第4年1月份的销售额为295000美元，你的预测误差是多少？如果你的误差比较大，Karen可能会对你的预测值和实际销售额之间的差异产生疑惑，你将如何消除她对预测方法的怀疑？

报告简述：

1、 将第2年和第3年的月份用13-24以及25-36表示，则可以得到时间序列图，仔细观察时间序列图，会发现数据有一个规律，即每年1月份销售额最高，然后逐步下降，到9月份最低，然后10月份反弹，逐步上升，因此我们得出结论存在月份的季节模式。而且，我们还发现，从每年的一月份销售额来看，呈现小幅增长趋势。可以推断时间序列同时包含趋势模式和季节模式。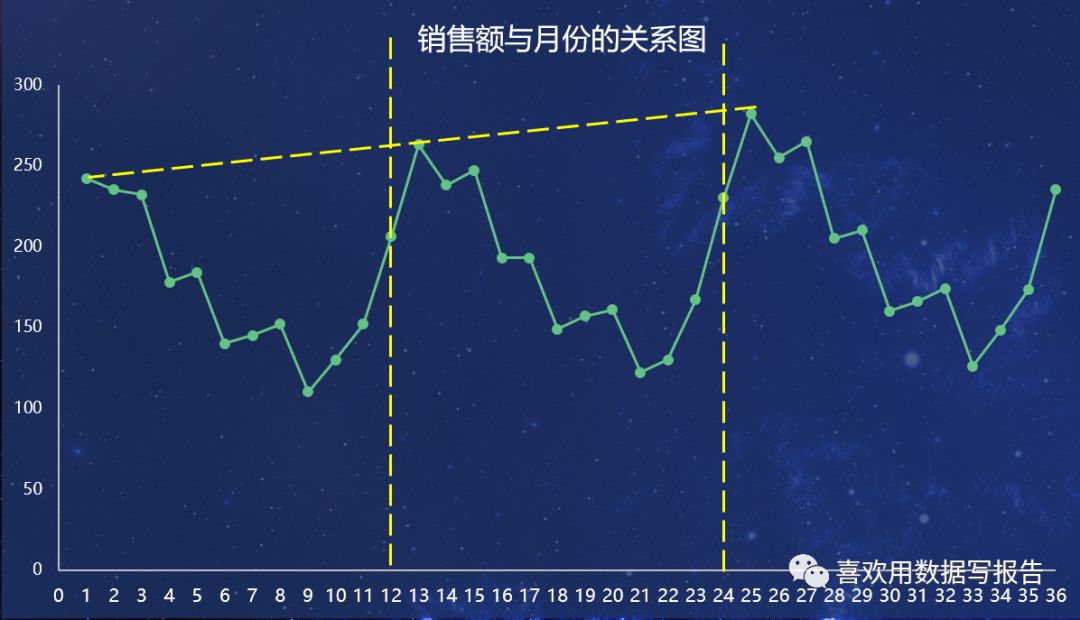

2、要计算季节指数，我们确定每月的季节影响所使用的计算程序是先计算移动平均数，从数据中剔除组合在一起的月份和不规则影响，留给我们的时间序列只包含趋势和移动平均没有剔除的随机波动。

由于我们所使用的是数据是月份时间序列，因此每一次移动平均数的计算中，我们使用12项数据（全年），第一个移动平均数 = SUM（第一年的销售额）/12 = 175.5，第一个移动平均数正好是第一年的平均月销售额，现在加上第二年的第一个月的销售额，去掉第一年的第一个月的销售额，得到第二个移动平均数，为177.25。

现在我们回顾计算结果，发现175.5这个数字位于第一年所有月份的中间，但是，12个月的移动平均数，不存在中间月份，因此，175.5应该对应于6.5月，即第6月的后半段和第7月的前半段，我们计算出的两个移动平均数并不能直接对应于时间序列的原始月份，因此，我们可以通过计算两个移动平均数的平均数来解决这个难题，这个移动平均数被称为中心化移动平均数，这应该是它精准的位置

我们利用公式识别出时间序列中月份-不规则的组合影响，例如，第一年第7月份的趋势值为176.375（中心化移动平均值），因此145/176.375=0.8221是月份-不规则的组合值

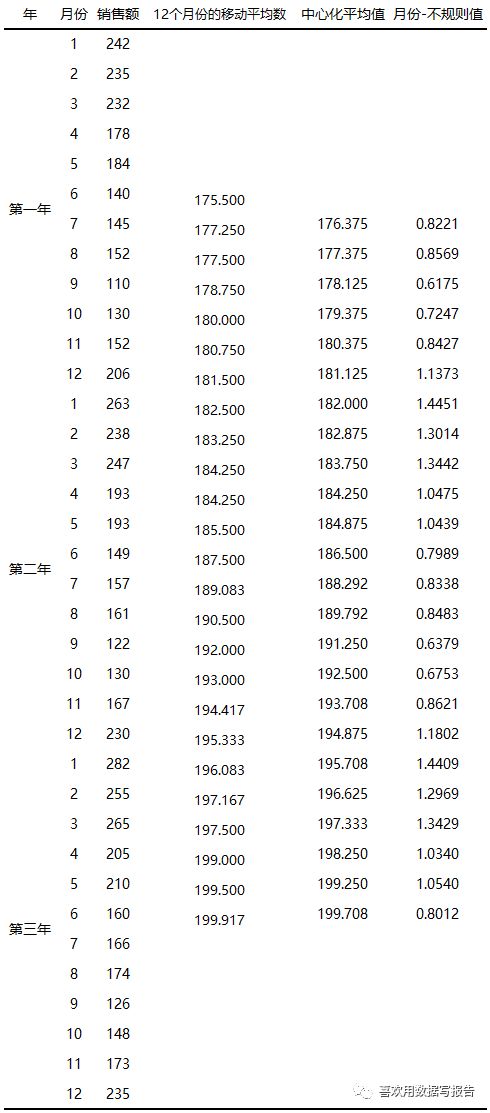
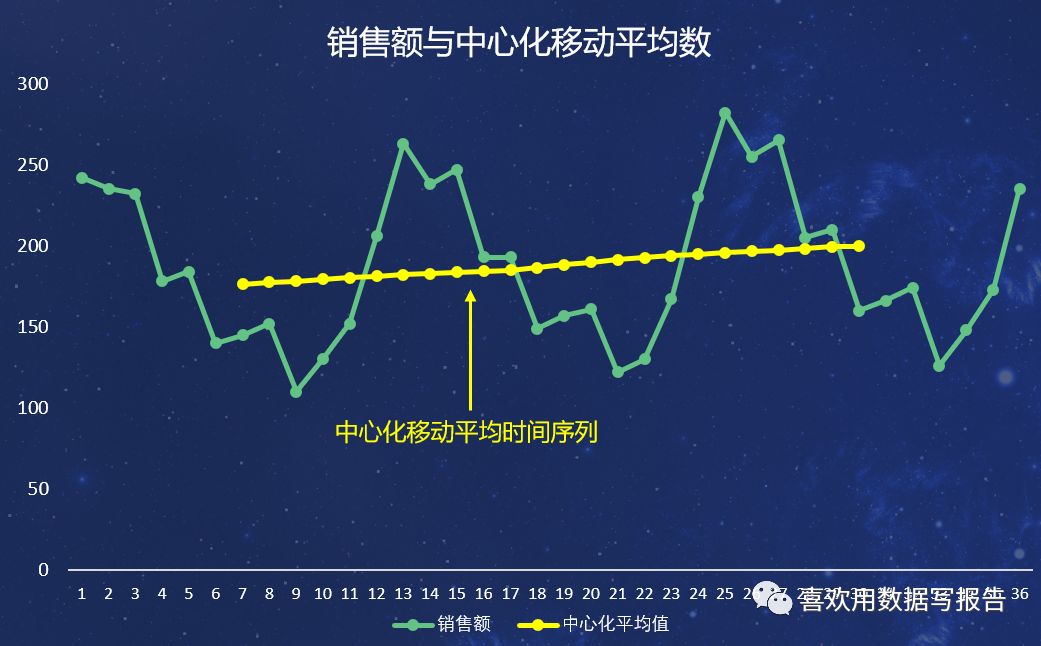
考虑第7月份的月份-不规则值0.8221和0.8338,月份-不规则值大于1表明影响在趋势估计之上，而小于1表明影响在趋势估计之下，因此，在7月份，两个月份-不规则值表现都低于平均水平的影响，因为月份-不规则值每年的波动主要是随机误差引起的，所以，我们可以取平均数以消除不规则的影响，从而得到7月季节影响的估计值

7月的季节影响值=（0.8221+0.8338）/2=0.828，我们将0.828称为7月份的季节指数，接下来汇总每个月的季节指数

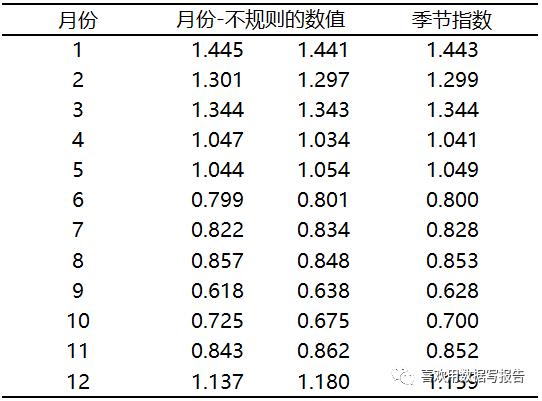
根据季节指数观测结果，最佳的销售月份是1月份，其销售额水平高出趋势估计44.3%，最差的是9月份，季节指数为0.628，表明其销售额水平低于趋势估计37.2%，季节指数直观的表明了每个月的销售水平。最后，由于季节指数之和等于12，因此符合乘法模型要求，不需要进行调整。

3、 接下来消除季节影响的时间序列，利用乘法分析模型，我们用每一个观测值除以相应的季节指数来消除时间序列的季节影响，可得表格如下

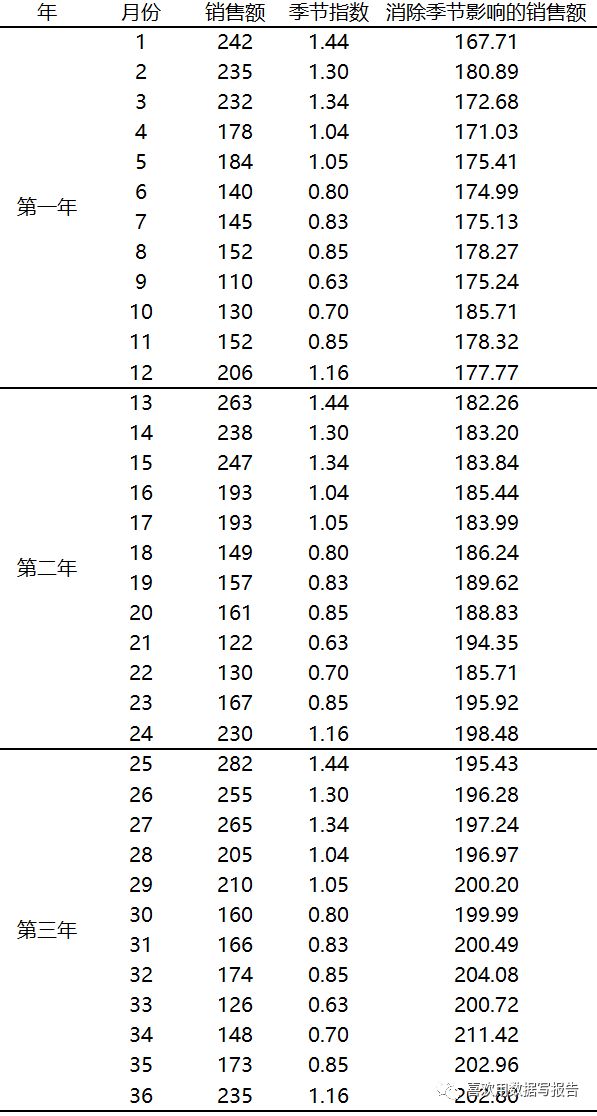
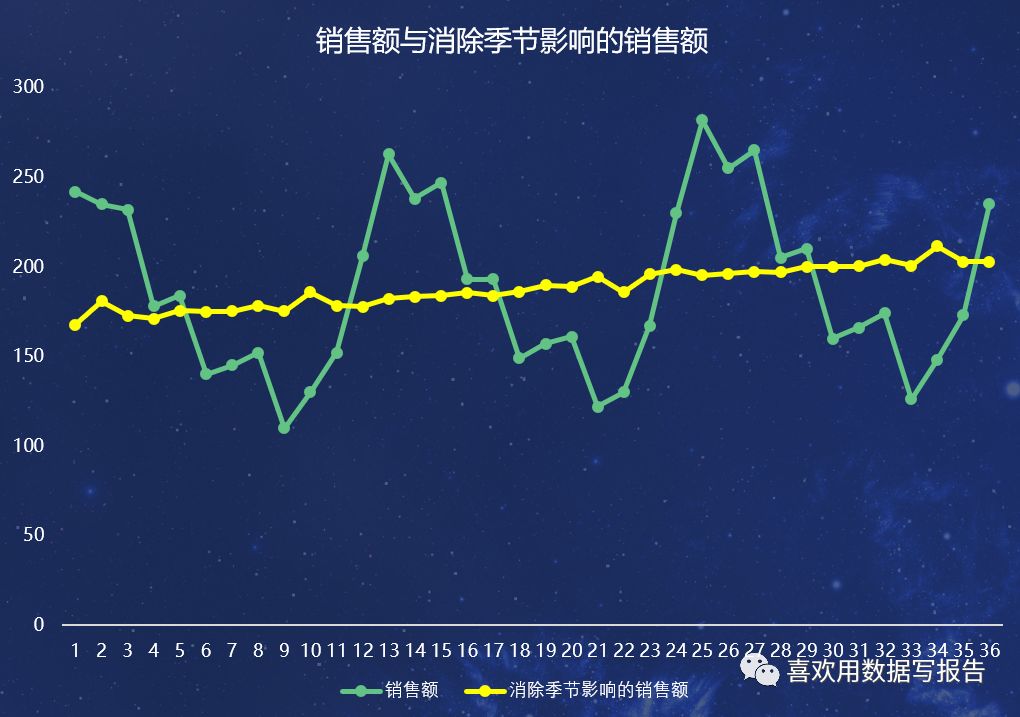
可以看到消除季节影响的销售额是一条有向上的线性趋势的时间序列，为了确定这个趋势，我们用一个线性趋势方程来拟合消除季节影响的时间序列，估计的线性回归方程可以表示为：

Y =b0 + b1X，其中Y是X的线性趋势预测值，b0是线性趋势的截距，b1是趋势线的斜率，X代表时期（月份），根据EXCEL可以求得方程Y = 1.0217X + 169.42 ，且判定系数为0.9204，是一个极佳的拟合

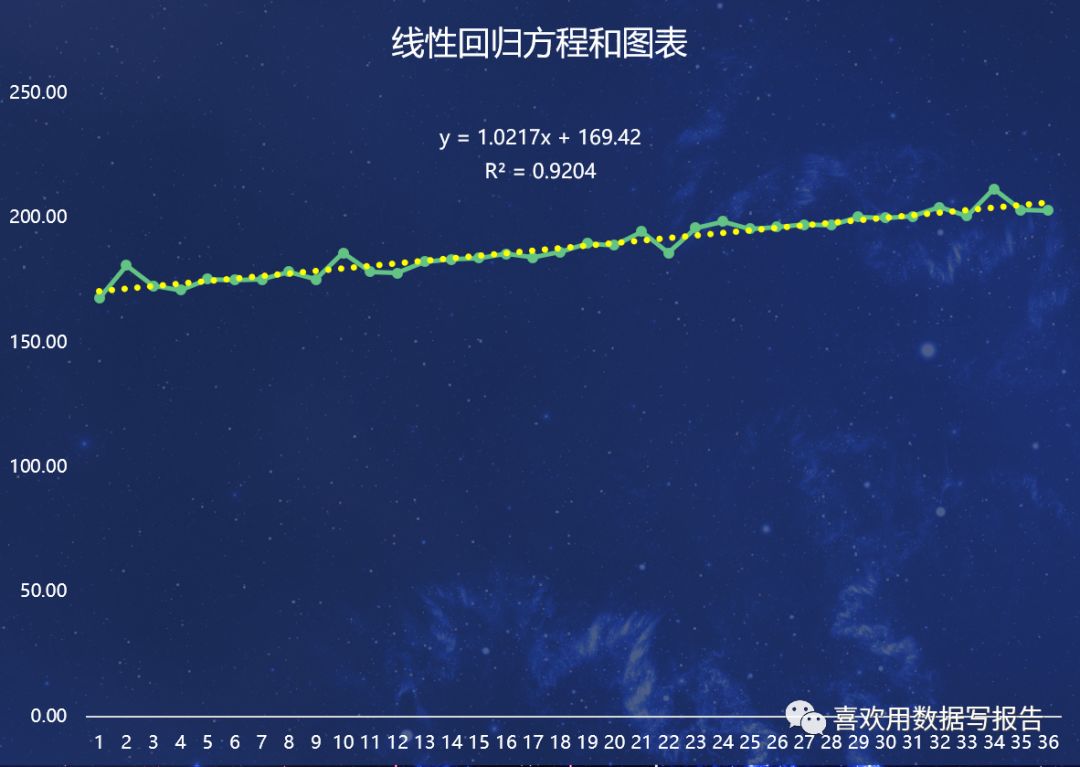
4、预测第4年1-12月的销售额，现在我们将37-48带入回归方程，首先将X=37（第4年1月份）带入方程得到Y的值为207.223，这个是消除季节影响的趋势预测值，我们用这个值再乘以季节指数1.44，得到该月份的预测值，于是，207.223*1.44=299.02  用表显示第4年的预测值如下

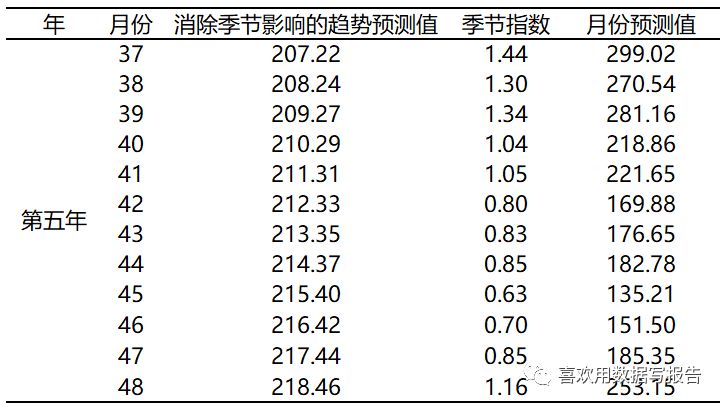
接下来，看一下预测值和观测值的直观图

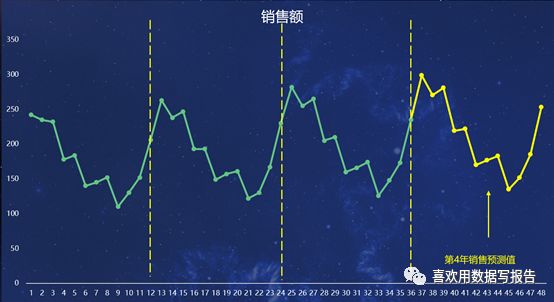
从图中可以看到第4年趋势基本与前三年保持一致

5、接下来利用虚拟变量回归法来求得第4年的预测值，首先建立时间序列的月份季节影响和线性趋势的多元回归方程的一般形式如下：

Y= b0+b1Qtr+b2Qtr+b3Qtr+…+bxt

由于有12个月份，因此我们建立11个Qtr，用表格显示为

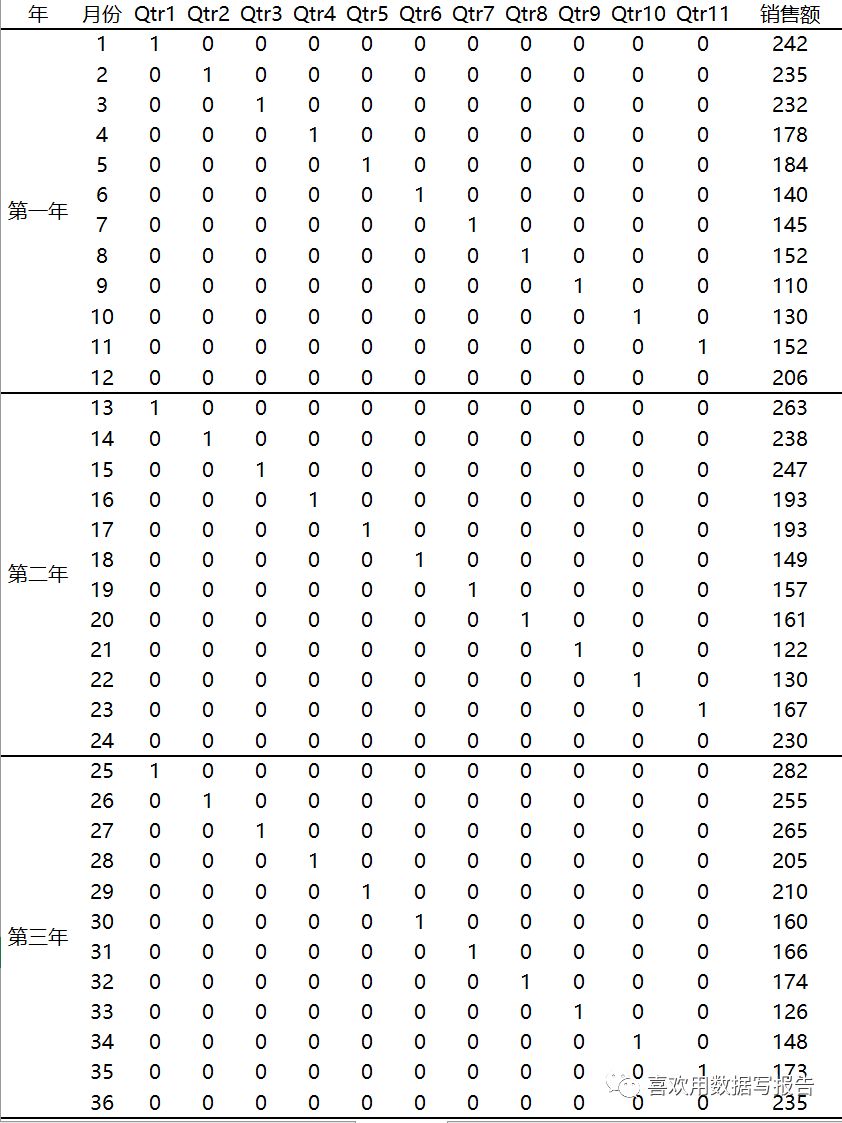
利用EXCEL得到回归方程：

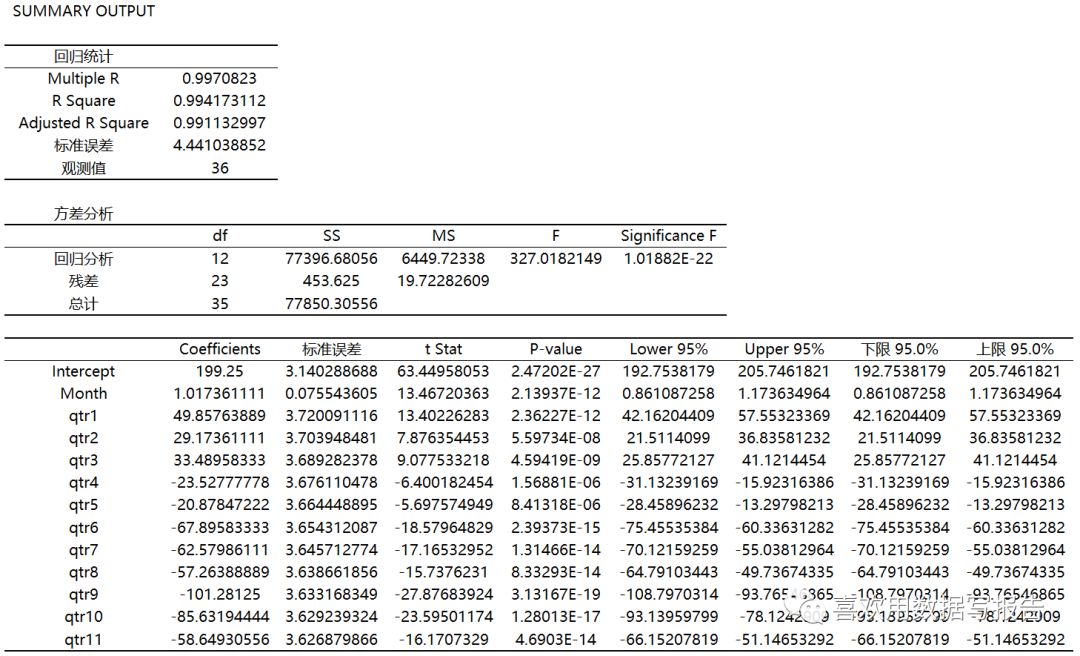
Y=199.25+1.017X+49.858Qtr1+…-58.65Qtr11

由于涉及大量的计算，就不一一显示了，将月份37（第4年第一个月）带入方程，得到预测值

Y=199.25+1.017*37+49.858= 286.75，以此内推，得到表格：

可以看出，两种方法得到的差异非常小，利用图表直观观测：

根据表格和图形可以看出，时间序列分解法的预测值在1-5月份和12月份大于虚拟变量回归法的预测值，但是在6-11月份小于虚拟变量回归法的预测值，而刚好大于的这六个月的季节指数全部为正数，虚拟变量回归法将预测值的变异性收缩了。

如果第4年1月份的销售额为295，则与时间序列分解法的值很接近，建议为时间序列分解法预测第4年的全部值。