时间序列的自回归模型—从线性代数的角度来看

Posted 2021-05-02 数学人生

文章链接：https://zhuanlan.zhihu.com/p/35093835

Fibonacci 序列

在开始讲解时间序列的自回归模型（AutoRegression Model）之前，我们需要先介绍一下线性代数的基础知识。为了介绍线性代数的基础知识，我们可以先看一个简单的例子。考虑整数序列 Fibonacci 序列，它的通项公式是一个递归函数，每项的取值是由前两项所生成的，其具体的公式就是

F(n) = F(n-1) + F(n-2)，

其初始值是 F(0) = 0, F(1) = 1。

按照其递归公式来计算，我们可以详细写出前面的几项，那就是：

0，1，1，2，3，5，8，13，21，34，55，89，144，...

但是，计算 Fibonacci 的通项公式则比计算等差数列和等比数列的通项公式复杂的多，因为这里需要使用线性代数的技巧才能解决这个问题。

总结

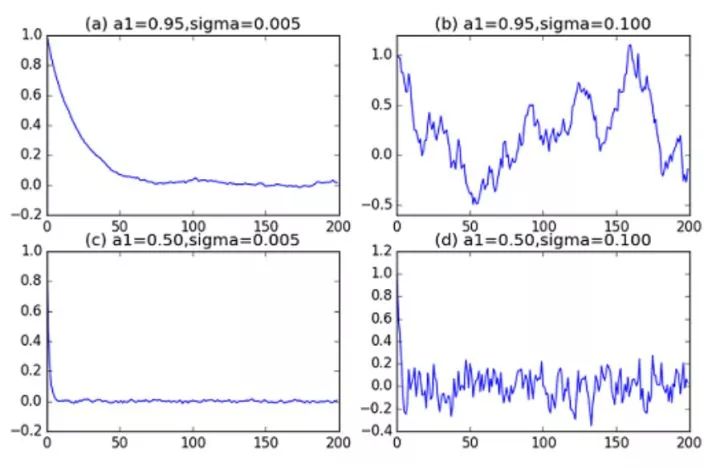
在本篇文章中，笔者从线性代数出发，介绍了矩阵求幂的一些方法，推导了 Fibonacci 数列的通项公式。然后从自回归模型的定义出发，介绍了它们的基本性质和它们与线性代数的联系。在未来的 Blog 中，笔者将会介绍时间序列的更多相关内容。

相关文章推荐：

1.

2.

3.

欢迎大家关注公众账号数学人生