用时间序列模型严肃证明A股收益率是0

Posted 2021-05-02 市场量化观察

肉眼即可发现，现在大盘三千多点，十几年前也是三千多点，但由此判断A股无收益缺乏学术严谨性。

本文对上证综指每月收益率建立线性时间序列模型，严肃掰扯这一论断。本文参考了《Analysis of Financial Time Series》(by RUEY S.TSAY)的方法，用R编程，并将该书对美国股指的研究结果拿来作对比。

PART1  准备数据

从Wind提取2000年1月至2018年5月上证综指每月末收盘价，计算较上月末的收益率，共221个样本点。直接对每月收益率画图如下：

总体来看，每月收益率一直围绕0值震荡，振幅基本在10%以内，2008年和2015年牛市附近振幅增大。

再放大看一下近几年的：

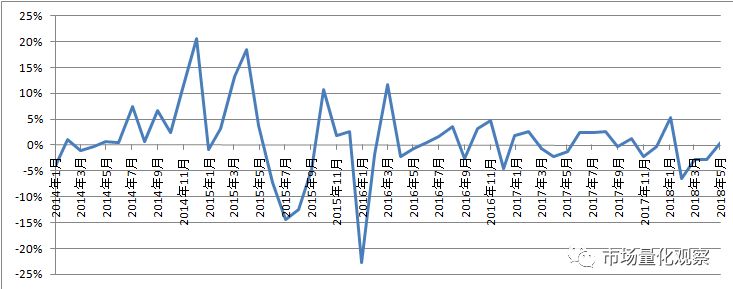
可见2016年下半年以来，每月收益率振幅下降，基本在(-5%,5%)区间内。

PART2  建立线形时间序列模型

步骤1，判断该序列是否具有自相关性，进行Box-Ljung检验，自由度选10，结果如下：

可以看到P-value非常小，即存在显著自相关性

直接对序列画自相关系数图(ACF)，结果如下：

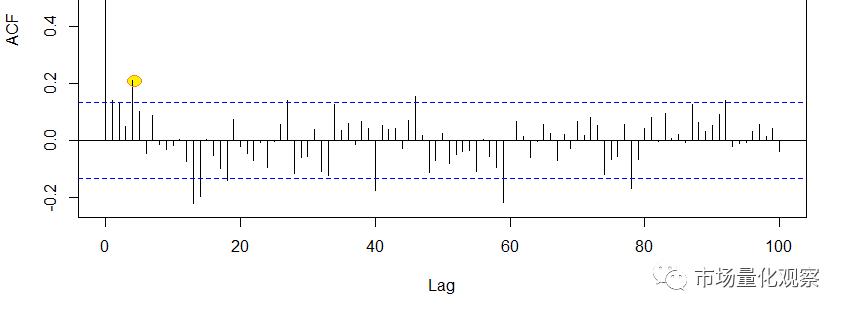
ACF图显示第4个相关系数（即当前收益率与4个月前收益率的相关系数）明显高出显著水平范围，再次印证了自相关性的存在

步骤2 判断模型阶数

下面需要判断建立多少阶（order）的模型，即用之前多少个月的收益率来预测当前收益率。阶数越高拟合效果越好，但会过度拟合，通用方法是计算增加阶数对最大似然值的贡献来确定阶数，常用的指标是AIC, AIC结果如下：

可以看到第4项是0（R把最小值调为0，便于观察），所以判断模型阶数是4

步骤3 拟和线性自相关模型

按照4阶来拟合模型，得到拟合系数结果如下，前4项是每个自变量的系数，最后的intercept是序列均值

检验一下模型的质量，检验的方法是对模型的残差进行Box-Ljung检验，看是否还存在自相关性，结果如下：

可以看到，对残差检验的P-value为0.72，非常不显著，说明残差已不存在自相关性，即模型解释了绝大部分自相关，模型质量可以接受

步骤4 模型解读

首先关注的是，intercept项，该项代表序列的均值

虽然均值为0.0071是正数，但标准差高达0.0083，也就说，我们实在无法拒绝这个假设：上证综指月度收益率均值是0！

另外我们看到，第4项的系数较大，也就是说本月收益率与4个月前的收益率相关性较大，其次是1个月前和2个月前，3个月前的收益率系数几乎为0, 可忽略。

步骤5 预测2018年6月收益率

把2018年2月-5月的收益率带入模型，预测结果如下：

按照该模型，2018年6月，上证综指将小幅下跌1%

从技术分析看，上证指数近日出现跳空缺口，下探到一个支撑线后小幅弹回震荡，按照模型预测结果，6月股指将在该支撑线附近继续小幅震荡或下跌。

PART3  与美国股指的对比

《Analysis of Financial Time Series》对美国1926-2008年每月的股指收益率建立了同样的模型，共计996个样本，采用了3阶模型，结果如下：

结果显示，美国股指月度收益率均值0.89%，而标准差仅为0.0017，我们在较高显著水平下可以拒绝该假设：美国股指月度收益是0。