时间序列分析----结合ARMA的卡尔曼滤波算法

Posted 2021-05-02 智能算法研究学习1688

https://zhuanlan.zhihu.com/p/23534595

卡尔曼滤波简介

卡尔曼滤波算法是通过系统输入输出观测数据（在本贴中为HS300日对数收益率），对系统状态进行最优估计的算法。由于观测数据中包括系统（市场）中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

卡尔曼滤波无论是在对过去值的估计（插值或平滑）、对现在值得估计（滤波）以及对将来值的估计（预测）方面都有着比较重要的作用。在本帖中主要介绍在预测方面的实现方法，希望能够给需要用到此类方法的矿友一些启发~

在将卡尔曼滤波算法与ARMA模型结合时，卡尔曼滤波算法可以在当获得一个新的数据点（）时，递归地更新状态变量（预测值）的信息，可以起到对ARMA模型的修正作用，在一定程度上提高ARMA模型的预测精度。

算法实现 part 1

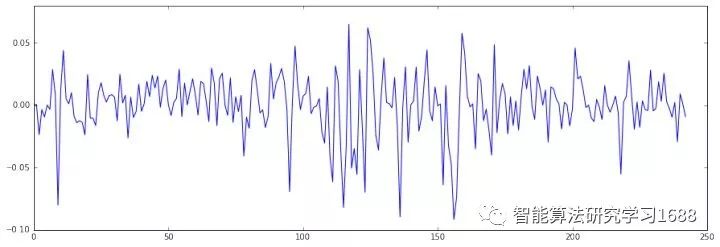
首先，提取，即HS300的日对数收益率

提取2015年去年HS300收盘价及对数收益率

一、状态空间模型与ARMA

要卡尔曼滤波，首先要引入状态空间模型。在这里，“状态”与“测量”相对，表示从数据中移除测量误差。
在介绍状态空间模型时，我们由浅入深，首先引入一元的局部趋势模型

1.1 局部趋势模型

首先考虑一元时间序列（HS300日对数收益率），局部趋势模型满足

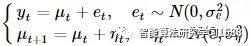
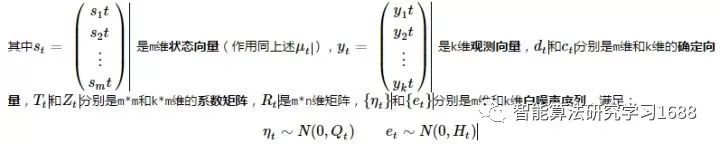
初始状态s1∼N(μ1|0,Σ1|0)，其中μ1|0，Σ1|0是给定的。

1.3 ARMA模型与线性状态空间之间的转换

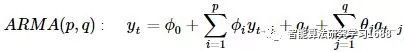
ARMA模型的详细解读请参照“金融时间序列入门（二）----MA & ARMA & ARIMA”
在下面的过程中，令=0（当≠0时，则在中将其减去，得到均值为0的），并令m=max(p,q+1)（后面的讨论中为了简便，只讨论令m=p的情况）
此时，可以令ARMA(p,q)=ARMA(m,m-1)，其中如m=q-1，则ϕp+1,⋯,ϕm=0；如m=p，则θq+1,⋯,θm−1=0

算法实现 part 2

下面进入ARMA模型的算法实现部分

ARMA模型：通过信息准则定阶（详细解读参照“金融时间序列入门（一））

('aic-order: ', (3, 2))
('bic-order: ', (2, 2))
('hqic-order: ', (2, 2))

bic与hqic均给出ar阶数为2，又根据前面假设：p >= q+1，故令order = (2,1)
ljung-box检验（检验残差序列是否存在滞后相关）

AC Q Prob(>Q)

lag 1.0 0.001445 0.000514 0.98192

2.0 0.018605 0.086024 0.957900

3.0 -0.002259 0.087289 0.993318

4.0 0.083168 1.810307 0.770596

5.0 0.051584 2.475918 0.780117

6.0 -0.096262 4.803670 0.569229

7.0 -0.006572 4.814565 0.682581

8.0 0.140752 9.833538 0.276904

9.0 -0.024263 9.983311 0.351838

10.0 -0.102196 12.651893 0.243791

11.0 -0.115016 16.046571 0.139411

12.0 0.072517 17.401897 0.135094

13.0 0.111749 20.634319 0.080483

14.0 -0.075790 22.127649 0.076029

15.0 -0.005695 22.136117 0.104284

16.0 0.097925 24.651090 0.076217

17.0 0.015490 24.714301 0.101290

18.0 -0.015433 24.777319 0.131174

19.0 -0.010715 24.807835 0.166965

20.0 0.114525 28.309448 0.102274

21.0 0.162293 35.372962 0.025685

22.0 -0.043516 35.883094 0.031254

23.0 -0.100106 38.594945 0.021968

24.0 -0.004349 38.600087 0.030066

25.0 0.055229 39.433107 0.033318

26.0 -0.130746 44.123087 0.014662

27.0 -0.055123 44.960590 0.016417

28.0 0.055733 45.820698 0.018188

29.0 0.085124 47.836577 0.015282

30.0 -0.133892 52.847294 0.006163

31.0 -0.093931 55.325033 0.004608

32.0 -0.033918 55.649630 0.005918

33.0 0.061328 56.715913 0.006285

34.0 0.107805 60.026497 0.003847

35.0 -0.060198 61.063710 0.004126

36.0 0.088619 63.322414 0.003275

37.0 0.056958 64.260011 0.003593

38.0 -0.013537 64.313233 0.004847

39.0 -0.017196 64.399532 0.006412

40.0 0.014103 64.457863 0.008440

通过ljung-box检验，判断残差序列是否存在滞后相关。得到滞后20阶以内的p-value均大于0.05，故可以判断残差中没有显著的序列相关性，可以进行下一步分析。

1.3.1 Harvey方法：推导

将ARMA转化为状态空间模型主要有Akaike、Harvey、Aoki三种方法，在这里只介绍较为常用的Harvey方法。1.3.1节的推导过程中公式较多，但逻辑清晰，读起来不会费力。不过侧重于应用的小伙伴可以跳过该节，直接看Harvey方法的结论与算法实现部分

推导过程如下：

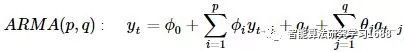
Harvey方法中，给出了具有m维状态向量的状态空间的一种形式，该状态向量的第一个元素是yt，的其他元素通过递归得到。 由ARMA(m,m-1):

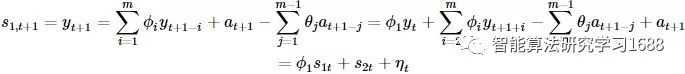
上式中：

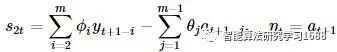
继续，考，可以得到：

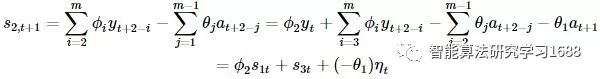
可以得到

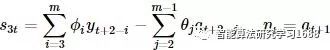
继续，可以得→⋯ 根据递归，有：

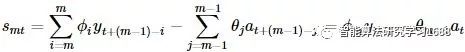
最终有

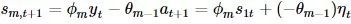
1.3.2 Harvey方法：结论

将上述方程综合起来，我们得到如下形式的状态空间模型：

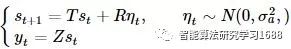
Qt=。在(3)式中，AR与MA的系数被直接用在了系统矩阵里。

算法实现 part 3

下面进入Harvey方法的算法实现部分，参见原文查看

二、结合ARMA模型的卡尔曼滤波算法

2.1 卡尔曼滤波基本公式

卡尔曼滤波（Kalman filter）的目标是：当获得一个新的数据点时，递归地更新状态变量的信息，即递归地得到在给定数据Ft=y1,⋯,yt条件下st+1的条件分布和模型。由于卡尔曼滤波早已有成型的公式，因此公式的推导过程在这里不做赘述，直接给出。
对于（2）式所给出的状态空间模型，给定初始值s1|0,Σ1|0，卡尔曼滤波的算法为（公式中上角标T表示转置）：

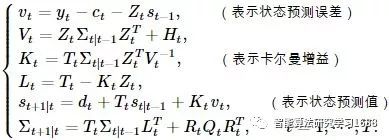
2.2 结合ARMA模型的卡尔曼滤波算法

对于由Harvey方法（即（3）式）所给出的状态空间模型，给定初始值s1|0,Σ1|0，卡尔曼滤波的算法为（公式中上角标T表示转置）：

其中T，R，Qt 均由Harvey方法给出。

确定初始值s1|0,Σ1|0的方法：

算法实现 part 4

下面进入卡尔曼滤波预测的算法实现部分

预测收益率一步涨跌准确率——ARMA + Kalman：0.555555555556

预测收益率一步涨跌准确率——ARMA：0.469135802469

可以看到，相比于ARMA模型的拟合结果，ARMA+卡尔曼滤波算法所得到的拟合结果更为平滑，说明在经过卡尔曼滤波调整之后，对于噪声过滤效果更好。因此，利用卡尔曼滤波对时间序列进行平滑是大有可为的。同时，在预测收益率一步涨跌时，ARMA+卡尔曼滤波算法相比于单纯的ARMA算法来说，准确度有了近10%的提高。虽然相对其他诸如机器学习等预测方法来说，预测准确度还不够，但卡尔曼滤波对于ARMA的调整效果值得借鉴。

参考文献

《金融时间序列分析》 第2版 Ruey S.Tsay著 王辉、潘家柱 译

其他文章推荐：

金融时间序列分析入门（一）

金融时间序列入门（二）----MA & ARMA & ARIMA 

金融时间序列入门（三）--- 季节模型

金融时间序列入门（四）--- ARCH、GARCH

基于时间序列的协整关系的配对交易

基于小波变换的时间序列预测

时间序列的小波去噪