浅谈时间序列分析

Posted 2021-05-02 KPMG大数据挖掘

在企业生产中经常会遇到这样的问题，某厂家月度供货量预测，某商场月度销售量的预测等等，这些往往和其之前的供货量、销售量有关，对这类问题的分析我们通常称为时间序列分析。

 一  平稳的时间序列模型

       只有平稳的时间序列才可以进行统计分析，因为平稳性保证了时间序列数据出自于同一分布，以便后续均值、方差、延迟k期协方差、延迟k期相关系数的计算。我们通常所说的平稳时间序列，是指对任意时间下，序列的均值、方差存在并为常数，且自协方差函数与自相关系数只与时间间隔k有关。 

好像没听懂？没关系，大多数建模软件都有平稳性检验的模块。如在Python中，可调用tseries中函数adfuller进行平稳性检验，如果p-value小于一定值（如5%）则拒绝非平稳假设，认为该数据是平稳的。

如果一个时间序列经证实为平稳时间序列，那么我们可以尝试采取以下几种模型进行建模。当然，模型有很多，本文就不一一介绍完全了。

 01  AR自回归模型

时间序列当期观测值Xt与前p期有线性关系，而与前p+1期及之后无线性关系，即：

确定p的方式有以下几种：

1）观察PACF几阶截尾；

2）AIC/BIC准则，且统计量的取值越小越好。

  02  MA滑动平均模型

时间序列当期观测值Xt与之前其时刻值Xt-1，Xt-2，… 无线性关系，而与前t-1，t-2，…t-q期进入系统的扰动项有一定的相关性，即：

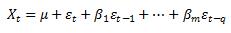
确定q的方式有以下几种：

1）观察ACF几阶截尾；

2）AIC/BIC准则，且统计量的取值越小越好。

  03  ARMA自回归滑动平均模型

将上述两个模型结合，即Xt不仅与以前时刻的自身值有关，还和其以前t-1，t-2，…t-q期进入系统的扰动项有一定的相关性，即：

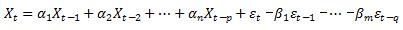
确定p,q的方式：AIC/BIC准则，且统计量的取值越小越好。

 二  非平稳的时间序列模型

如果一个时间序列经证实是非平稳的，那么ARMA模型就不能直接运用了，我们需要他的兄弟——ARIMA模型来帮助我们。

ARIMA模型

ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model，简记ARIMA)。是由博克思(Box)詹金斯(Jenkins)于70年代初提出的一种著名时间序列预测方法，所以又称为box-jenkins模型、博克思一詹金斯法。

ARIMA模型有三个参数: p,d,q。其中：

•p--代表预测模型中采用的时序数据本身的滞后数(lags) ,也叫做AR/Auto-Regressive项；

•d--代表时序数据需要进行几阶差分化，才是稳定的，也叫Integrated项；

•q--代表预测模型中采用的预测误差的滞后数(lags)，也叫做MA/Moving Average项。

ARIMA(p,d,q)模型实质是先对非平稳的历史数据Yt进行d次差分处理得到新的平稳的数据序列Xt，将Xt拟合ARMA(p,q)模型，然后再将原d次差分还原，便可以得到Yt的预测数据。

是不是很简单？当然，时间序列建模方式有很多，ARIMA是其中常用的一种，其建模过程大体可概括为以下几步，你学会了吗？

① PACF（Partial Autocorrelation Function），即偏自相关函数：用于描述时间序列中在任意两个时间间隔k的时刻，去除1至k-1这个时间段的其他数据的相关系数。

②ACF（Autocorrelation Function），即自相关函数：用于描述事件序列中任意两个时间间隔为k的相关系数。

---

参考资料：《Python数据科学 技术详解与商业实践》常国珍、赵仁乾、张秋剑 2018年7月 第1版

长按二维码即可关注！也请随手推荐我们给你的小伙伴 ↓↓↓↓