时间序列数据之一二三阶指数平滑法（Python代码）

Posted 2021-05-02 校苑数模

基本概念

时间序列数据：

是指一个数据序列，在时域上存在相互依赖的关系

前提假设：

时间序列分析一般假设我们获得的数据在时域上具有一定的相互依赖关系，例如股票价格在t时刻很高，那么在t+1时刻价格也会比较高（跌停才10%）；如果股票价格在一段时间内获得稳定的上升，那么在接下来的一段时间内延续上升趋势的概率也会比较大。

目标：

（1）发现这种隐含的依赖关系，并增加我们对此类时间序列的理解；

（2）对未观测到的或者尚未发生的时间序列进行预测。

我们认为时间序列由两部分组成：有规律的时间序列（即有依赖关系）+噪声（无规律，无依赖）。所以，，接下来要做的就是过滤噪声—接下来利用指数平滑来对数据进行处理

不管是几阶指数平滑，都需要设置初值，设置初值的方法：

假如数据大于20项，那么初值就可以认定为第一个数据；假如数据小于20项，就取待处理数据的前三项的真实平均值作为初始值

一阶指数平滑

一次指数平滑一般应用于直线型数据，且一次指数平滑具有滞后性，可以说明有明显的时间性、季节性。

一次指数平滑需要滞后一期，给定平滑系数alpha，那么一次指数平滑的计算公式为：

预测第t+1期的数值则是上一期的实际值与预测值的加权平均，预测公式为：

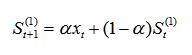
代码实现

二阶指数平滑

二次指数平滑一般也应用于直线型，但是效果会比一次指数平滑好很多，也就相当于加强版的一次指数平滑。

给定平滑系数alpha，那么二次指数平滑的计算公式为：

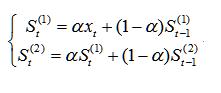
预测未来t期的值X{t+T}的计算公式为：

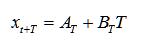
其中：

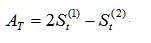
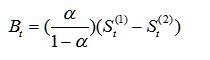
平滑之前的数据如下图所示：

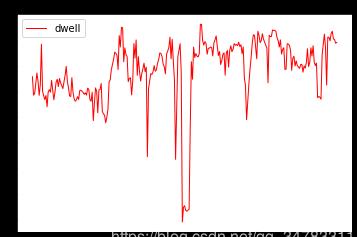
二阶指数平滑之后的效果如下图所示：

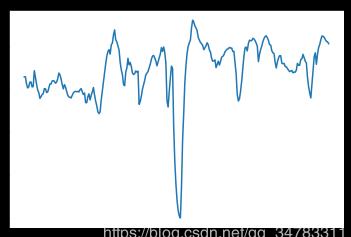
三阶指数平滑(holt-winters)

适用：

三阶指数平滑法针对有趋势也有季节性的序列。当一个序列在每个固定的时间间隔中都出现某种重复的模式，就称之具有季节性特征，而这样的一个时间间隔称为一个季节(理解：比如说在一个周内，销量呈现出重复的模式)。一个季节的长度k为它所包含的序列点个数。

二次指数平滑考虑了序列的baseline和趋势，三次就是在此基础上增加了一个季节分量。类似于趋势分量，对季节分量也要做指数平滑。比如预测下一个季节第3个点的季节分量时，需要指数平滑地考虑当前季节第3个点的季节分量、上个季节第3个点的季节分量。

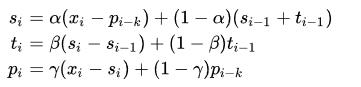
其中：

P_i 是指周期性部分，公式如下：

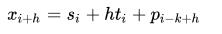
k表示这个周期的长度

代码实现如下

运行代码

画图代码

平滑之前的数据如下图所示：

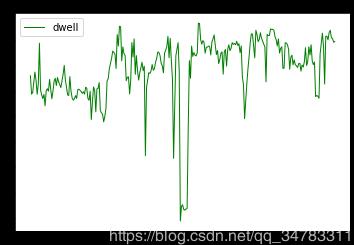
平滑之后的数据如下图所示：

--------------------- 

来源：CSDN 

原文：

https://blog.csdn.net/qq_34783311/article/details/84723480