时间序列分析第二章 滞后算子

Posted 2021-05-02 痕风雨

        选首张黑洞照片做封面只为纪念 和......蹭热度？？？？？

        前一章我们运用矩阵代数的方法对差分方程进行了讨论，本章将引入时间序列算子的相关概念，并使用时间序列算子来继续对差分方程进行讨论。

一、时间序列算子(滞后算子)

        一般而言，我们常见的时间序列

可以视为一个无限时间序列的观测样本，常记为：

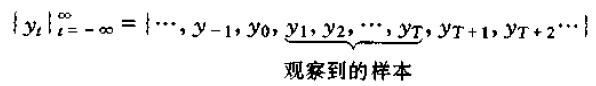
我们将引入的时间序列算子就是对这样的无限时间序列进行运算。

        类比函数y=f(x)或y=g(x,w)是将一个输入x或者一组输入(x,w)通过一定处理而得到输出y的过程，时间序列算子是将一个时间序列或一组时间序列变为一个新的时间序列的操作。如乘法算子：

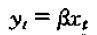
注意，不要将其与普通标量的乘法等同，这实际上是一个无限乘法序列的简写。对每一个时间t都有这样一个乘法式子将相应的xt转化为yt。还有一个加法算子也是常用的：

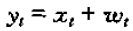
加法算子将两个时间序列xt与wt作为输入，将相应时间点上的x与w相加输出新的时间序列yt。很容易验证：

=

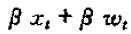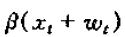
下面我们引入之后算子的概念：

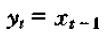
很明显，在每一个时间t上，该算子将x在时间t-1上的取值赋给y在t上的取值，这个算子我们一般记为L，即：

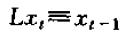
下面我们考虑对时间序列xt进行两次之后运算的结果：

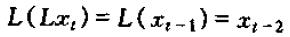
进行两次滞后运算可以即为L2，即：

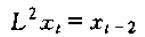
一般而言，进行k次滞后运算可以记为Lk，即：

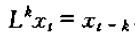
可以简单验证以下两个等式：

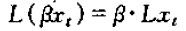
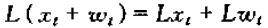
所以，在时间序列运算中，我们可以将L像乘法运算进行各种转化，如：

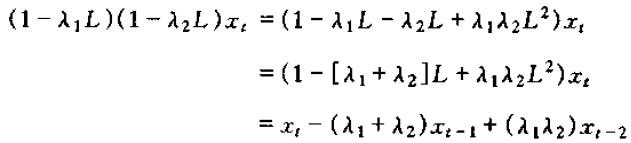
二、一阶差分方程

        对于一阶差分方程：

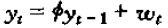
我们可以用滞后算子将其改写为：

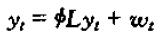
或者

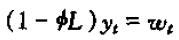
接下来，我们在上式的左右两边同乘：

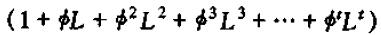
即有

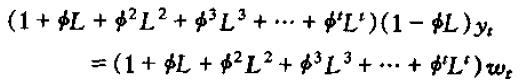
其中，上式左边的滞后多项式展开：

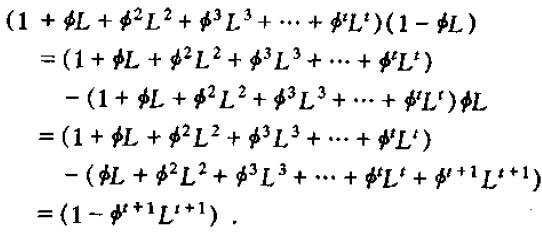
带回去，即有

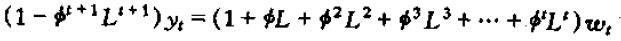
或

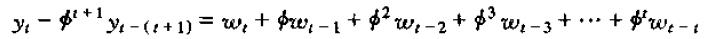
进一步

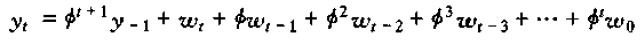
得到一个似曾相识的式子，这就是上一章中我们通过递归运算得到的一阶差分方程的解。上面的推导过程中，我们知道有

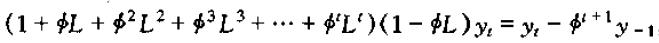
如果其中|Φ|<1且y-1有界，则当t不断增大趋于无穷时，有：

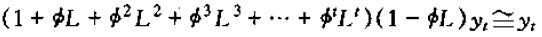
因此，我们定义一个特殊的滞后算子

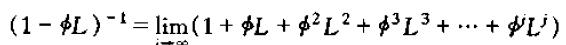
在|Φ|<1且时间序列有界的条件下，它满足

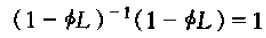
即

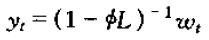
三、二阶差分方程

        对于二阶差分方程

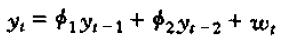
用滞后算子改写为

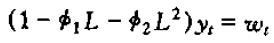
可以将左边的滞后多项式进行因式分解

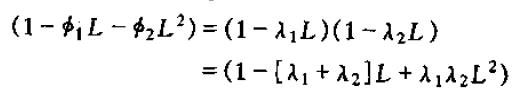
其中，λ1和λ2可以通过解一元二次方程：

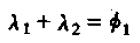
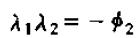
求解。这和我们学一元二次方程时根与系数的关系很相似，所以这个求解过程似乎和解某个一元二次方程相似。由第一章的学习我们知道，求解矩阵

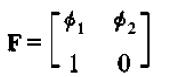
的特征值时就需要解一元二次方程

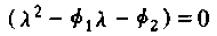
那么我们不禁要问，二者是否等同？答案是肯定的。可以证明，我们有以下结论：

        对以下滞后多项式的进行因式分解

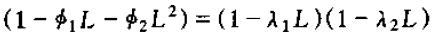
其中λ1与λ2的计算与求解矩阵F的特征值是同一个运算过程，并且F的特征值λ1，λ2与因式分解得到的λ1，λ2是相同的。

        我们知道，只有当F的两个特征值的模均小于1时，二阶差分方程才是稳定的，这意味着方程

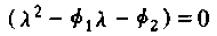
的根均位于单位圆内时，二阶系统稳定。这等价于方程

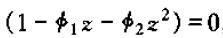
的根位于单位圆外时，二阶系统稳定。

        假定二阶差分方程是稳定的，基于前面定义的特殊算子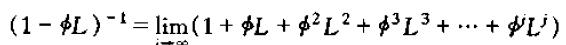

我们有

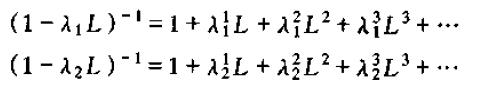
从而对于

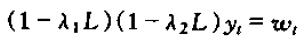
两边同乘

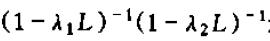
可得

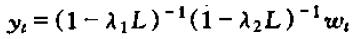
当λ1与λ2不相等时，我们有

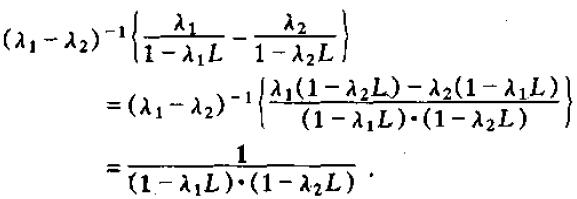
从而

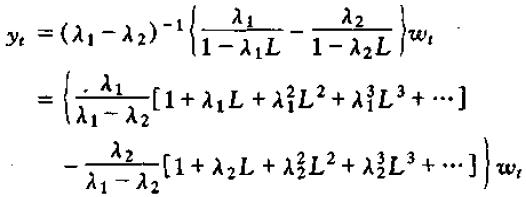
或

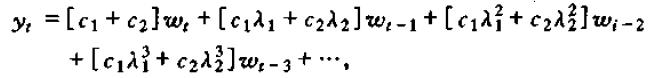
其中

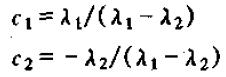
从而，动态乘子为

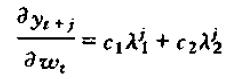
这与第一章中的推导是一致的。

四、P阶差分方程

        类比二阶差分方程的处理方法，我们将P阶差分方程：

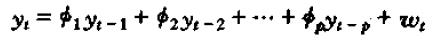
改写为

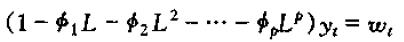
同样地，对左边的滞后多项式进行因式分解：

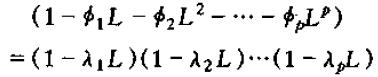
其中(λ1,λ2,λ3,...,λp)的求解与求矩阵

的特征值相同，即解方程

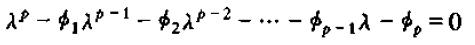
当该方程的根都落在单位圆内，则P阶差分方程稳定，这等价于方程

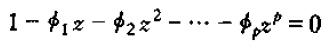
的根均落在单位圆外，则P阶差分方程稳定。

        下面假定P阶差分方程稳定，F的所有特征值不相等，则

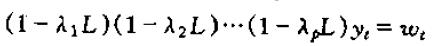
可以改写为

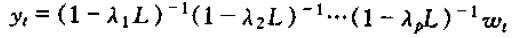
对等式右边的滞后多项式进行变换，则上式可以写为

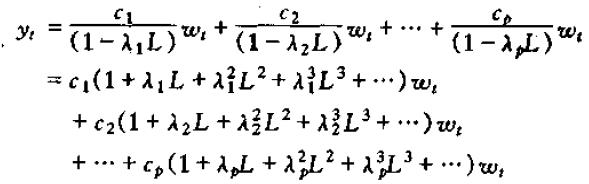
或

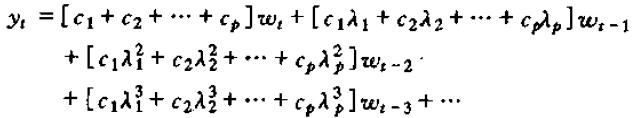
其中

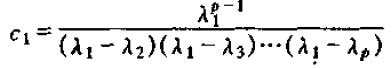
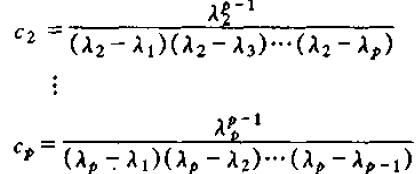
从而可以得到动态乘子为：

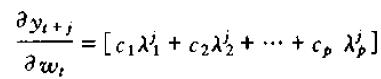
        进一步，p阶差分方程最终可以表示为如下形式

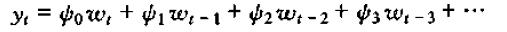
其中

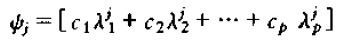
进一步改写为

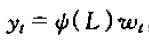
其中

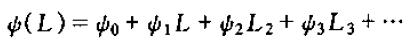
我们知道，wt对y的现值的影响的表达式为：

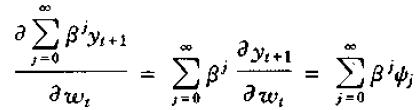
将ψ(L)中的L换为β，我们有

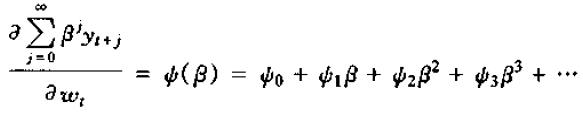
由于

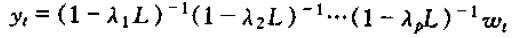
所以

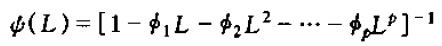
从而

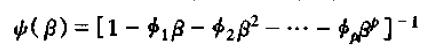
进而

令β=1，我们可以得到wt对y的影响的长期效应为