平稳时间序列分析之模型识别

Posted 2021-05-02 医数思维云课堂

作者丨梅子

来源丨医数思维云课堂（ID:Datamedi）   

 

时间序列识别过程利用自相关系数ACF和偏自相关系数PACF，其中ACF用于衡量序列中较早的数据值是否与后面时间值有某种关系，PACF用于捕获变量和变量滞后量之间的关系。

计算出样本自相关系数和偏相关系数的值之后，就要根据它们表现出来的性质，确定相应的p，q的数值，从而选择适当阶数的 ARMA(p,q)模型。因此，模型识别过程也称为模型定阶过程。

01

ARMA模型定阶的基本原则

自相关系数	偏自相关系数	模型
拖尾	P阶截尾	AR(p)
q阶截尾	拖尾	MA(q)
拖尾	拖尾	ARMA(p,q)

由于样本的随机性，样本的自相关系数不会呈现出理论截尾的完美情况，本应截尾的样本自相关系数或偏自相关系数人会呈现小值振荡。同时，由于平稳时间序列通常都具有短期相关性，随着延迟阶数k的增大，样本自相关系数或偏自相关系数都会衰减至零值附近作小值波动。

这种现象促使我们必须思考：

（1）当样本自相关系或偏自相关系数在延迟若干阶之后衰减为小值波动时，什么情况下该看做相关系数截尾？

（2）什么情况下该看做相关系数在延迟若干阶之后衰减到零值附近作拖尾波动？

这实际上没有绝对的标准，很大程度上依靠分析人员的主观经验。但样本自相关系数和偏自相关系数的近似分布可以帮助分许人员做出尽量合理的判断。

如果样本自相关系数或偏相关系数在最初的d阶明显超过2倍标准差范围，而后几乎95%的自相关关系都落在2倍标准差范围以内，而且由非零自相关系数衰减为小值波动的过程非常突然，这时，通常视为自相关系数截尾，截尾阶数为d。

如果有超过5%的样本系数落入2倍标准差范围之外，或者有显著非零的自相关系数衰减为小值波动的过程比较缓慢或者非常连续，这时，通常视为自相关系数不截尾。

02

案例分析

选择合适的ARMA模型拟合1880——1985年全球气表平均温度改变值差分序列。

①读入数据，绘制时序图

a<-read.table("average_temp.txt",header=T)

dif_x<-ts(diff(a[,2]),start=1880)

plot(dif_x,col="blue")

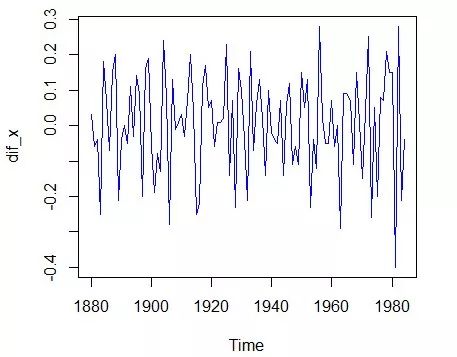
②白噪声检验

for(i in 1:2) print(Box.test(dif_x,lag=6*i))

可看到P值小于0.05，序列非白噪声。

③绘制自相关图和偏自相关图

acf(dif_x)

pacf(dif_x)

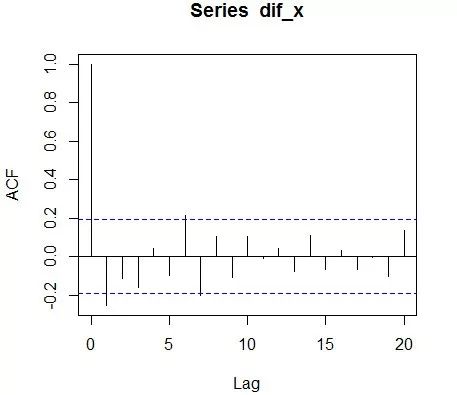
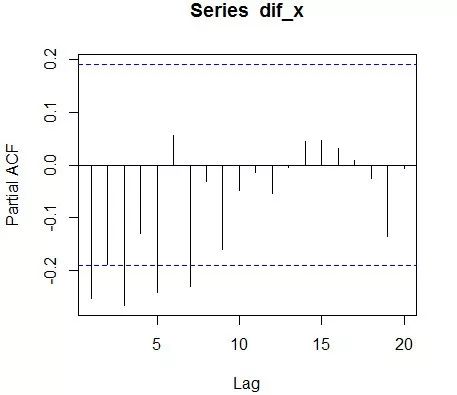
自相关系数和偏自相关系数均显示出不截尾的性质，因此可以尝试用ARMA（1,1）拟合该序列。

为了尽量避免因个人经验不足而导致的模型识别不准确的问题， R 提供了函数 auto.arima（）。该函数基于信息量最小原则自动识别模型阶数，并给出该模型的参数估计值。 要使用该函数，必须先下载 zoo 和forecast 程序包。

auto.arima 函数的命令格式为：

auto.arima (x , max.p=5 , max.q= , ic=）

x:需要定阶的序列名。

max.p:自相关系数最高阶数，系统默认为5。

max.q:移动平均系数最高阶数，系统默认为5。

ic:指定信息准则。有“AICC”、“AIC”、“BIC”.系统默认为AIC准则。

利用auto.arima 函数定阶1880——1985年全球气表平均温度改变值的MRMA模型。

library(zoo)

library(forecast)

auto.arima(dif_x)

结果如下：

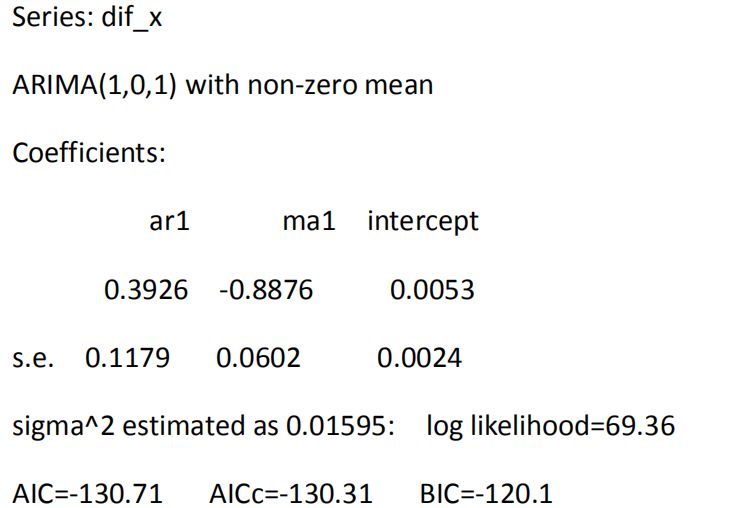
从上述结果可看出系统自动定阶的结果与我们根据自相关图和偏自相关图定阶的结果一致。

想要了解更多，可以点击阅读全文哦。

往期推荐

点击图片直达原文

►关注医数思维云课堂——医数思维云课堂（ID:Datamedi），每周四20：00准时更新课程，陪60万医学生共同成长，转载请联系我们授权。

觉得“好看”，请点这里↓↓↓