时间序列预测必备背景知识（Part5）

Posted 2021-05-02 kaggle竞赛宝典

这是我写的第二十一篇文章， 本文是关于时间序列处理的。本文接着上文继续介绍第五章（也是最后一章了），文章中有一些公式部分为了方便大家阅读直接进行了截图，如果觉得阅读不方便的话可以去文末下载notebook本地打开学习，注:本文的内容90%是翻译《Forecasting: Principles and Practice》,链接为:http://otexts.org/fpp2/intro-reading.html的,里面穿插了些许自己的理解,建议英文好的可以直接去阅读原书籍。  

    补充：有些读者反映阅读时，显示不方便，如果出现该问题，大家用电脑的浏览器打开应该就可以解决该问题了，每篇文章对应的PDF或者Notebook都会在文末提供下载,也可以下载进行学习......

本系列一共介绍5块内容,本篇文章我们重点看第五章节的内容

• 1  时间序列预测简介(Introduction)

• 2  时间序列可视化

• 3  判断预测法(Judgmental forecasts)

• 4  线性回归模型

• 5  时间序列分解

• 5.1  时间序列成份

• 5.2  移动平均值

• 5.3  经典的分解

• 5.4  X11分解

• 5.5  SEATS 分解

• 5.6  STL(Seasonal and Trend decomposition using Loess)分解

• 5.7  使用分解的预测

• 5.8  深入阅读

5  时间序列分解

时间序列数据可以呈现大量的形式,将时间序列数据分成诸多模块对于时间序列问题的分析十分有帮助.

在第二章中,我们将时间序列分割成趋势,季节性,和周期性,平时我们经常将趋势和周期组合成"trend-cycle"成分,所以我们也可以将时间序列分割为三大块:"trend-cycle"模块,季节性模块和剩余组件(包含时间序列中的任何其他内容).

这一章,我们考虑从时间序列中提取这些成份的一些方法,通常这是为了帮助我们更好的理解时间序列,但是它也可以被用来提升我们的预测准确率.

5.1  时间序列成份

这一节主要介绍两种将时间成份的建模形式,加法模式和乘法模式.

两种时序模型

假设$y_t$是在时间段$t$处的数据,$S_t$为在时间段$t$处的季节性成份,$T_t$为趋势周期成份,$R_t$为在时间段$t$处的剩余成份.那么

• 加法模型:$y_t = S_t + T_t + R_t$,如果季节性波动是在周期趋势上下进行,那么加法模型是一个不错的选择.

• 乘法模型:$y_t = S_t * T_t * R_t$.如果波动和时间序列的level成比例相关,那么乘法模型会比较好.

加法模型和乘法模型的联系:$y_t = S_t * T_t * R_t$ = $logy_t = logS_t + logT_t + logR_t$

An alternative to using a multiplicative model is to first transform the data until the variation in the series appears to be stable over time, then use an additive model. When a log transformation has been used, this is equivalent to using a multiplicative decomposition because

例子

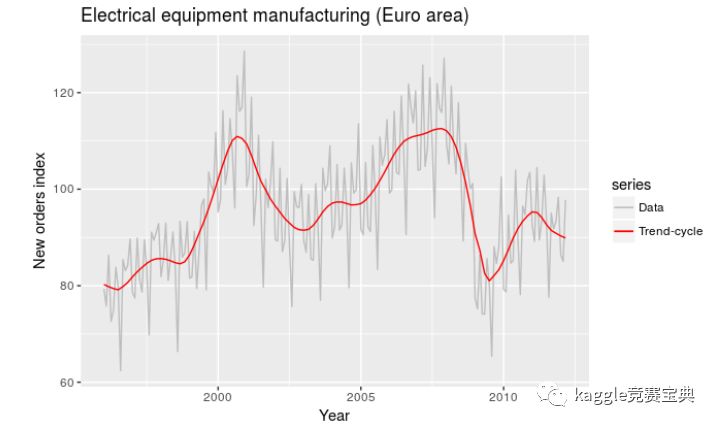
上图中$T_t$为趋势周期成份,$y_t$为原始数据成份,趋势周期展示了时间序列的整体运动(忽略季节性和任何小的波动).我们将加法模型的成份展开得到下图:

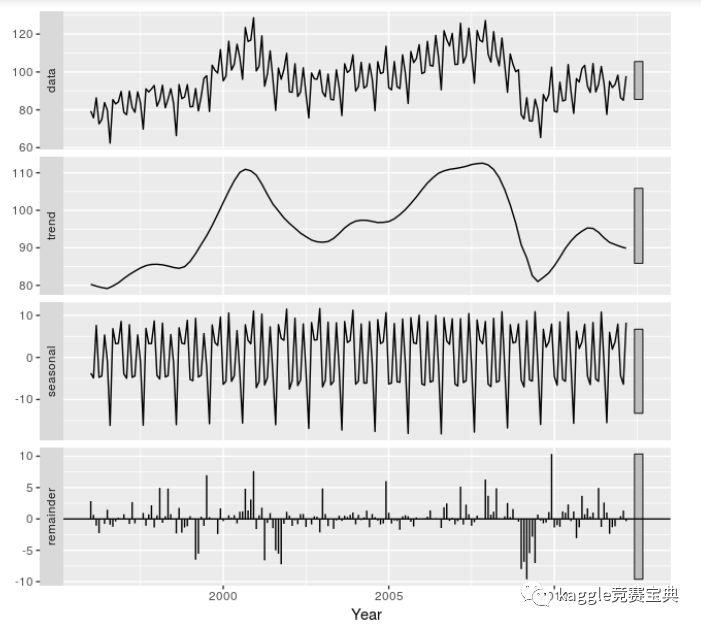
经季节性因素调整后的数据

• 定义:

经季节性因素调整后的数据： 如果我们将原始数据中的季节性因素移除,那么最终剩下的数据就被称作是季节性调整后的数据.对于加法模型,季节性调整后的数据可以通过$y_t - S_t$得到,对于乘法模型,可以通过$y_t / S_t$得到.

If the seasonal component is removed from the original data, the resulting values are called the “seasonally adjusted” data.

• 使用场景

如果季节性带来的波动不是我们感兴趣的,那么就可以对经季节性因素调整后的数据进行分析,例如,我们对于每个月的失业率非常感兴趣,但是因为每年的毕业季就会出现大量的失业,这种季节性带来的影响往往会阻碍我们发觉真正的潜在带来失业的原因,所以使用经季节性因素调整后的数据往往会更好.

5.2  移动平均值

在经典的分解模型中,第一步往往是使用移动平均值来估计趋势和周期(trend-cycle),所以这一节我们介绍最经典的移动平均值.

移动平均平滑

m-MA:一个阶数为$m$的易懂平均可以被表示为, $\bar{T}_t = \frac{1}{m} \Sigma_{j=-k}^{k} y_{t+j}$, 其中 $m=2k+1$, 也就是说我们希望利用均值来删除数据的随机扰动,是的我们的趋势周期(trend-cycle)能够更加平滑.当$m$越大,我们的移动均值就平滑.

• 使用季节性的数据估计趋势周期:

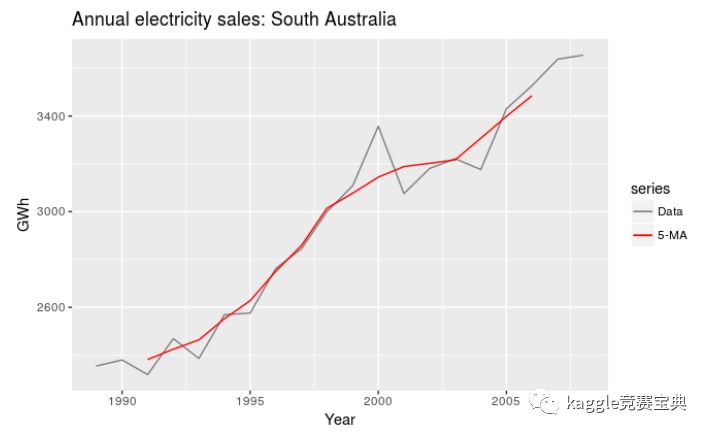
注意:移动均值法没有在$t$趋近于时间序列末尾的时候还给出估计$\bar{T}_t$,以你为红色的线没有延伸到边角. 

移动平均的移动平均

• 移动平均的移动平均可以看做是二阶信息.

• 中心移动平均线,当一个2-MA在一个偶数阶移动均值(例如4)之后的平均,我们就称之为:阶为4的中心移动平均. 可以表示为:

In general, an even order MA should be followed by an even order MA to make it symmetric. Similarly, an odd order MA should be followed by an odd order MA.

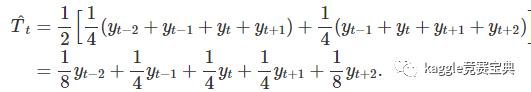
使用季节性的数据来估计趋势周期

使用上面$2*4-MA$的图,我们有:

我们发现,当使用季度性的数据时,每年的每个季度会给第一个最后一个数据相

同的权重,因为他们在一年中是连续的(今年的季末和明年的季初),所以最终结

果带来的影响可以认为是没有季节性的波动存在的. 

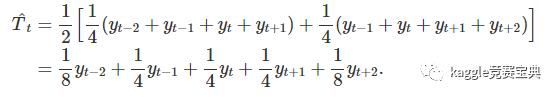
加权移动平均

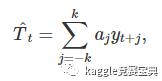
$\Sigma_{j=-k}^k a_j = 1$ 同时 $a_j = a_{-j}$,

• 优势:主要的优势在于加权移动平均可以获得一个平滑的趋势周期估计.

A major advantage of weighted moving averages is that they yield a smoother estimate of the trend-cycle. Instead of observations entering and leaving the calculation at full weight, their weights slowly increase and then slowly decrease, resulting in a smoother curve.

• 常用的一些权重:

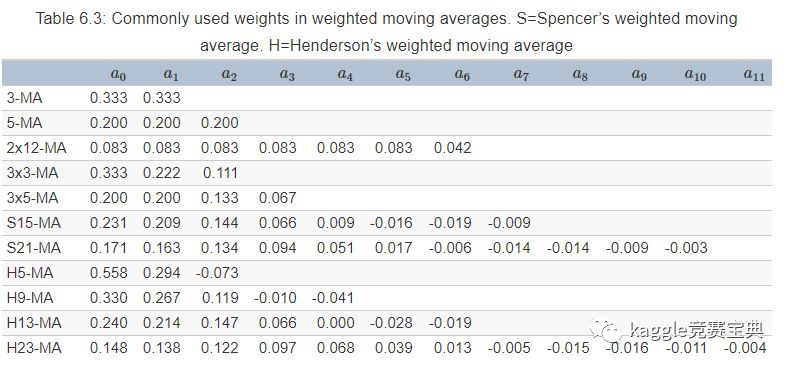
5.3  经典的分解

时间序列的分解是非常经典的一种思路,包括现在的Facebook的Prophet方法等,都是采用分解的形式建模,可解释性强,调参也方便.这一节我们假设季节性的成份年年都是一个常数,分解形式.

加法分解

步骤1：如果$m$是一个偶数,那么我们就使用$2*m-MA$来计算趋势周期成份$\bar{T}_t$,如果$m$是一个奇数,那么我们就使用$m-MA$来计算趋势周期成份$\bar{T}_t$.

步骤2:计算去趋势序列$y_t - \bar{T}_t$.

步骤3:为了估计每个季节的季节成份,我们直接对去趋势的数据求均值,例如,计算三月的季节成份,我们就对所有历史上去趋势的三月的数据求均值.季节性的成份可以通过将数据每一年的的值链接起来获得.这样我们就可以得到$\bar{S}_t$.

步骤4:我们将数据减去趋势周期值和季节值得到我们的剩余部分,$\bar{R}_t = y_t - \bar{T}_t - \bar{S}_t$.

乘法分解

乘法分解和加法分解较大的区别就是将减替换为除即可.

经典分解评论

虽然经典的分解方法还常常被使用,但是它却存在非常多的缺点。

1. 趋势周期的估计在一些地方无法估计,例如时间序列的开始和时间序列的结尾处都无法计算,所以相应的,这些点的剩余成份和季节性成份都无法计算.

2. 趋势周的估计很容易太过平滑.

3. 经典的分解假设季节性的成份年年会重复,这对于很多长的时间序列并不是一个非常好的假设.

For example, electricity demand patterns have changed over time as air conditioning has become more widespread. Specifically, in many locations, the seasonal usage pattern from several decades ago had its maximum demand in winter (due to heating), while the current seasonal pattern has its maximum demand in summer (due to air conditioning).

有时,时间序列的值在一小部分时期可能特别不寻常.而经典的分解方法对此却不是很鲁邦.

E.g., the monthly air passenger traffic may be affected by an industrial dispute, making the traffic during the dispute very different from usual. The classical method is not robust to these kinds of unusual values.

5.4  X11分解

上一节介绍的经典分解模型非常简单易懂,同时也有很多缺点,针对这些缺点,这一节我们介绍X11算法,X11算法再很多层面都解决了上述经典分解算法出现的问题.

X11 分解是基于经典的分解思路,但是却包含了更多的额外步骤和特征,在X11算法中,趋势周期估计在样本的开始和结尾都可以得到,季节性的成份也可以是随着时间缓慢变化的,此外X11还可以解决交易日的波动,节假日的影响以及一些其他因素的影响.

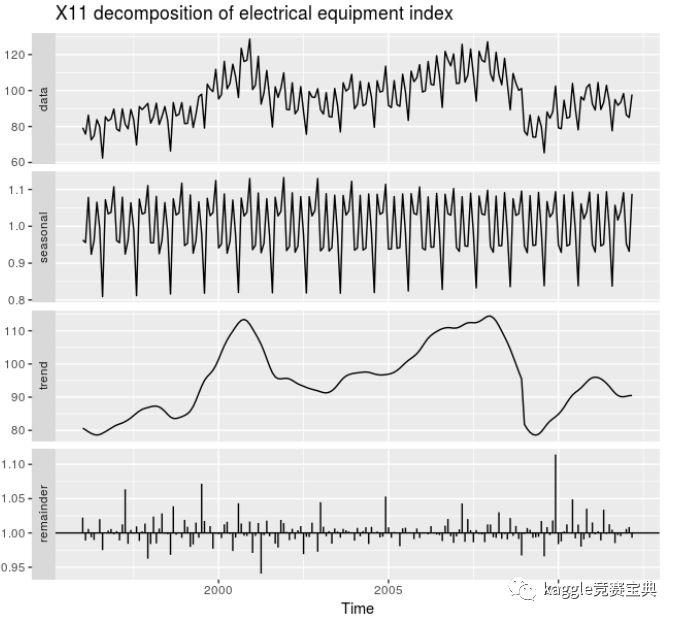
1. 相比于STL以及传统分解的方法,X11趋势周期部分很好的抓住了数据在2009年的突然下降的情况.

2. 在2009年末不同寻常的样本点在剩余成份也越加清晰.

5.5  SEATS 分解

SEATS 分解表示的是 "Seasonal Extraction in ARIMA Time Series",该过程是在西班牙银行开发的,但是该过程仅仅在季度和月度数据中可行,所以诸如日数据或者小时数据等则需要另外一套方法.关于该方法的讨论,关于该方法的详细讨论可以参考下面的文献:

1. Dagum, Estela Bee, and Silvia Bianconcini. 2016. Seasonal Adjustment Methods and Real Time Trend-Cycle Estimation: Springer.

5.6  STL分解

STL（Seasonal and Trend decomposition using Loess）是一个分解时间序列的多功能并且鲁棒的方法,相比于SEATS和X11分解方法,STL方法拥有如下的优势和缺点:

优点 :

1. 不像SEATS和X11方法,STL可以处理任意类型的季节性性,不仅仅是月和季度的数据;

2. 季节性的成份可以随时间变化,变化率也可以被用户所控制;

3. 趋势周期的平滑性可以被用户所控制;

4. 对奇异值鲁邦(i.e. 用户可以指定一个鲁棒的分解),因此偶尔的不寻常的样本点不会影响趋势周期和季节性的成份,但是还是会影响剩余成份.

缺点:

1. 无法自动处理交易日和日历波动;

2. 仅提供对于加法分解的形式(虽然可以通过对数据进行log处理来获取乘法分解)

当使用STL时,两个需要被选择,一个是趋势周期窗口,另外一个是季节性窗口,这两个窗口控制了趋势周几和季节性乘法的变化快慢.(窗口越小,变化越快).

5.7  使用分解的预测¶

因为这一节的内容就是前面的时间序列分解,所以此处不再多提,将书中比较重要的一部分截图如下.

5.8  深入阅读

A detailed modern discussion of SEATS and X11 decomposition methods is provided by Dagum and Bianconcini (2016). Cleveland et al. (1990) introduced STL, and still provides the best description of the algorithm. For a discussion of forecasting using STL, see Theodosiou (2011).

1. Dagum, Estela Bee, and Silvia Bianconcini. 2016. Seasonal Adjustment Methods and Real Time Trend-Cycle Estimation: Springer.

2. Cleveland, Robert B, William S Cleveland, Jean E McRae, and Irma J Terpenning. 1990. “STL: A Seasonal-Trend Decomposition Procedure Based on Loess.” Journal of Official Statistics 6 (1): 3–73.

3. Theodosiou, Marina. 2011. “Forecasting Monthly and Quarterly Time Series Using STL Decomposition.” International Journal of Forecasting 27 (4): 1178–95.

关于时序的基础的5章内容已经全部放在了一起，如需下载直接去下方的Github上面下载即可。希望本系列能帮助大家在做时序问题时能带来帮助。

https://github.com/dayeren/Kaggle_Competition_Treasure/tree/master/Models/Time_Series