SOM-VAE:时间序列的可解释离散表示学习
Posted 人工智能学术前沿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SOM-VAE:时间序列的可解释离散表示学习相关的知识,希望对你有一定的参考价值。
SOM-VAE:时间序列的可解释离散表示学习
题目:
SOM-VAE: Interpretable Discrete Representation Learning on Time Series
Vincent Fortuin, Matthias Hüser, Francesco Locatello, Heiko Strathmann, Gunnar Rätsch
来源:
Accepted for publication at the Seventh International Conference on Learning Representations (ICLR 2019)
Machine Learning (cs.LG)
Submitted on 6 Jun 2018
文档链接:
arXiv:1806.02199
代码链接:
https://github.com/JustGlowing/minisom
https://github.com/ratschlab/SOM-VAE
摘要
高维时间序列在许多领域都很常见。由于人类的认知并没有优化到能够很好地在高维空间中工作,这些领域可以从可解释的低维表示中获益。然而,大多数时间序列数据的表示学习算法都很难解释。这是由于从数据特性到表示的突出属性的非直观映射和非平滑性。为了解决这一问题,我们提出了一种基于可解释离散维数约简和深层生成建模思想的表示学习框架。该框架允许我们学习时间序列的离散表示,从而产生具有优越集群性能的平滑且可解释的嵌入。提出了一种克服离散表示学习不可微性的新方法,提出了一种基于梯度的传统自组织映射算法,该算法比原算法具有更高的性能。此外,我们在表示空间中集成了一个马尔可夫模型,以为了进行概率解释,。该模型揭示了时间转换结构,进一步提高了集群性能,并提供了额外的解释性见解和不确定性的自然表示。我们评估模型的聚类性能和可解释性静态(Fashion-)MNIST数据、时间序列的线性插值(Fashion-)MNIST图像,一个混乱的洛伦茨吸引子与两个宏观状态系统,以及一个具有挑战性的应用在医学界的时间序列eICU数据集。我们学习的表示方法与竞争对手的方法相比更有优势,并且便于在真实世界数据上执行下游任务。
英文原文
High-dimensional time series are common in many domains. Since human cognition is not optimized to work well in high-dimensional spaces, these areas could benefit from interpretable low-dimensional representations. However, most representation learning algorithms for time series data are difficult to interpret. This is due to non-intuitive mappings from data features to salient properties of the representation and non-smoothness over time. To address this problem, we propose a new representation learning framework building on ideas from interpretable discrete dimensionality reduction and deep generative modeling. This framework allows us to learn discrete representations of time series, which give rise to smooth and interpretable embeddings with superior clustering performance. We introduce a new way to overcome the non-differentiability in discrete representation learning and present a gradient-based version of the traditional self-organizing map algorithm that is more performant than the original. Furthermore, to allow for a probabilistic interpretation of our method, we integrate a Markov model in the representation space. This model uncovers the temporal transition structure, improves clustering performance even further and provides additional explanatory insights as well as a natural representation of uncertainty. We evaluate our model in terms of clustering performance and interpretability on static (Fashion-)MNIST data, a time series of linearly interpolated (Fashion-)MNIST images, a chaotic Lorenz attractor system with two macro states, as well as on a challenging real world medical time series application on the eICU data set. Our learned representations compare favorably with competitor methods and facilitate downstream tasks on the real world data.
要点
在这项工作中,我们提出一个新的深层架构,学习拓扑可解释离散表示的概率方式。提出了一种克服离散表示学习体系结构不可微性的新方法,开发了一种基于梯度的经典自组织映射算法,提高了算法的性能。我们从基准数据集,一个具有混沌行为的综合动力系统和真实世界的医学数据,为模型s在合成和真实世界时间序列上的性能提供了广泛的经验证据。
我们的主要贡献是
设计了一种新的时间序列可解释离散表示学习框架
结果表明,表示学习体系结构中的潜在概率模型提高了时间序列表示的聚类性和可解释性。
在基准数据和真实世界医疗数据集上显示了该模型优越的聚类性能,并在此基础上简化了后续任务。
图1:模型架构的示意图概述。数据空间(绿色)中的时间序列由神经网络(黑色)逐点编码到潜在空间中。利用自组织映射(SOM)逼近潜在数据流形[红色]。为了实现离散表示,每个潜在数据点(ze)都映射到SOM (zq)中最近的节点。学习了一个马尔可夫转移模型[蓝色]来预测给定当前离散表示(zqt)的下一个离散表示(zqt+1)。离散表示可以被另一个神经网络解码回原始数据空间。
图2:训练了512个嵌入点,从somo - vae的潜在空间切片生成的图像MNIST。它给出了高维潜在空间中数据流形的离散二维表示。

表1:我们的方法与一些基线在不同基准数据集上的纯度和标准化互信息方面的性能比较。用星号标记的方法是我们所提议的方法的变体。这些值是10次运行的平均值和各自的标准错误。每一种方法都适用于16个嵌入式/集群。
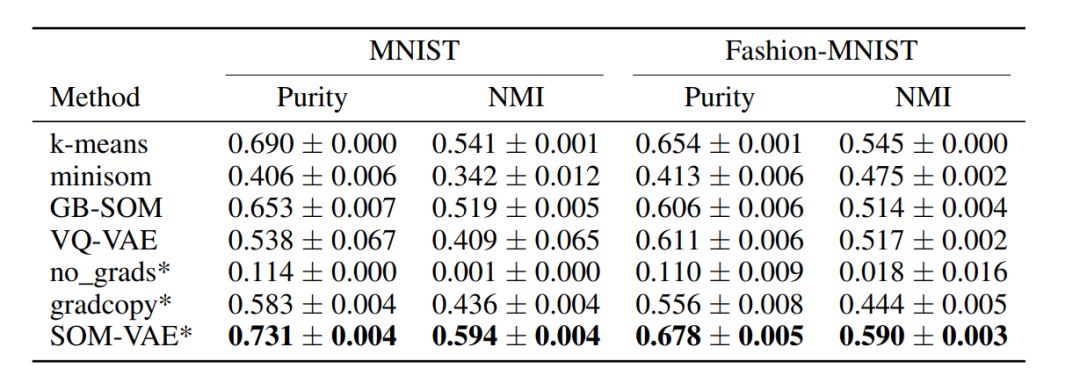
表2:基于不同基准数据集的纯度和归一化互信息,有无潜在马尔可夫模型(SOM-VAUE_prob)与k均值的性能比较。这些值是10次运行的平均值和各自的标准错误。每个方法都适用于64个嵌入式/集群。
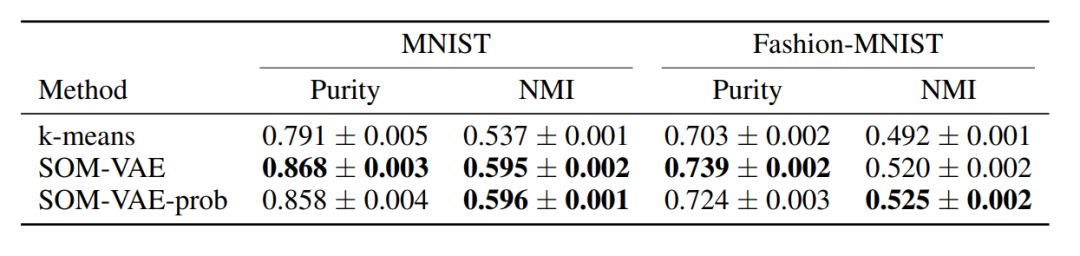
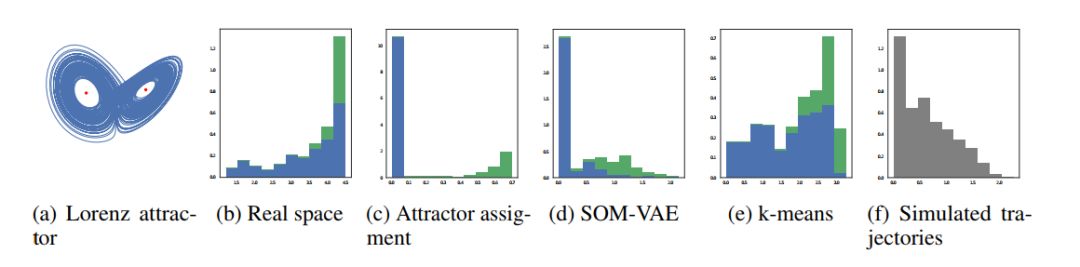
图3:洛伦兹吸引子子轨迹上熵分布的直方图(x轴上的熵)
文字来源于网络 侵删
翻译:人工智能学术前沿
加关注
qq群号:966308496
人工智能学术前沿
长按左边二维码
感谢您的关注
以上是关于SOM-VAE:时间序列的可解释离散表示学习的主要内容,如果未能解决你的问题,请参考以下文章