python实践——时间序列分析建模理论及代码实现
Posted AI蜗牛车
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了python实践——时间序列分析建模理论及代码实现相关的知识，希望对你有一定的参考价值。
声明：本文所讲的时间序列分析并不是指pandas的时间序列处理方法，pandas时间序列处理更缺确切地说时间序列的可视化、窗口移动操作等一些操作的统称。本文所讲的时间序列分析指的是一种算法，一种通过序列本身所潜在的规律去预测未来某个时刻可能发生的状况。
python时间序列分析
目录
一 什么是时间序列
二 为什么要用python
三 环境配置
四 时间序列分析
4.1 基本模型
4.2 pandas时间序列操作
4.3 平稳性检验
4.4 平稳性处理
4.5 模型识别
4.6 样本拟合
4.7 完善ARIMA模型
4.8 滚动预测
4.9 模型序列化
五 总结
01
什么是时间序列
时间序列简单的说就是各时间点上形成的数值序列，时间序列分析就是通过观察历史数据预测未来的值。在这里需要强调一点的是，时间序列分析并不是关于时间的回归，它主要是研究自身的变化规律的（这里不考虑含外生变量的时间序列）。
02
为什么用python
现在各类编程语言都有专门的时间序列分析开源框架或者是专门处理的相关程序库，处理时间序列最多的是使用MATLAB，因为它现成的工具函数，只需要使用几句话就可以实现一个时间序列建模模型。而我之所以选择python来实现，用两个字总结“情怀”，爱屋及乌，个人比较喜欢python，就用python撸了。能做时间序列的软件很多，SAS、R、SPSS、Eviews甚至matlab等等，实际工作中应用得比较多的应该还是SAS和R，前者推荐王燕写的《应用时间序列分析》，后者推荐“基于R语言的时间序列建模完整教程”这篇博文（翻译版）。python作为科学计算的利器，当然也有相关分析的包:statsmodels中tsa模块，当然这个包和SAS、R是比不了，但是python有另一个神器：pandas！pandas在时间序列上的应用，能简化我们很多的工作。
03
环境配置
python推荐直接装Anaconda，它集成了许多科学计算包，有一些包自己手动去装还是挺费劲的。statsmodels需要自己去安装，这里我推荐使用0.6的稳定版，0.7及其以上的版本能在github上找到，该版本在安装时会用C编译好，所以修改底层的一些代码将不会起作用。
04
时间序列分析
自回归移动平均模型(ARMA(p，q))是时间序列中最为重要的模型之一，它主要由两部分组成：AR代表p阶自回归过程，MA代表q阶移动平均过程，其公式如下：
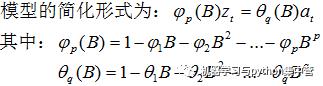
依据模型的形式、特性及自相关和偏自相关函数的特征，总结如下：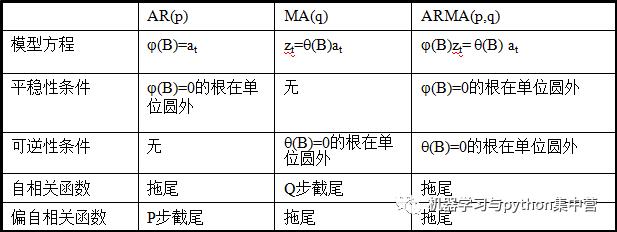 
在时间序列中，ARIMA模型是在ARMA模型的基础上多了差分的操作。
大熊猫真的很可爱，这里简单介绍一下它在时间序列上的可爱之处。和许多时间序列分析一样，本文同样使用航空乘客数据（AirPassengers.csv）作为样例。
数据读取：
# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pylab as plt
# 读取数据，pd.read_csv默认生成DataFrame对象，需将其转换成Series对象
df = pd.read_csv('AirPassengers.csv', encoding='utf-8', index_col='date')
df.index = pd.to_datetime(df.index) # 将字符串索引转换成时间索引
ts = df['x'] # 生成pd.Series对象
# 查看数据格式
ts.head()
ts.head().index
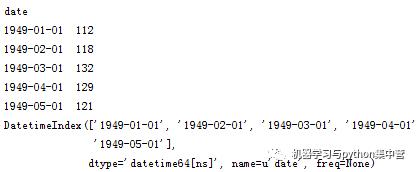
查看某日的值既可以使用字符串作为索引，又可以直接使用时间对象作为索引
ts['1949-01-01']
ts[datetime(1949,1,1)]
两者的返回值都是第一个序列值：112
如果要查看某一年的数据，pandas也能非常方便的实现
ts['1949']
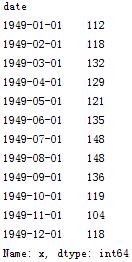
切片操作：
ts['1949-1' : '1949-6']
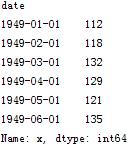
注意时间索引的切片操作起点和尾部都是包含的，这点与数值索引有所不同
pandas还有很多方便的时间序列函数，在后面的实际应用中在进行说明。
我们知道序列平稳性是进行时间序列分析的前提条件，很多人都会有疑问，为什么要满足平稳性的要求呢？在大数定理和中心定理中要求样本同分布（这里同分布等价于时间序列中的平稳性），而我们的建模过程中有很多都是建立在大数定理和中心极限定理的前提条件下的，如果它不满足，得到的许多结论都是不可靠的。以虚假回归为例，当响应变量和输入变量都平稳时，我们用t统计量检验标准化系数的显著性。而当响应变量和输入变量不平稳时，其标准化系数不在满足t分布，这时再用t检验来进行显著性分析，导致拒绝原假设的概率增加，即容易犯第一类错误，从而得出错误的结论。
平稳时间序列有两种定义：严平稳和宽平稳
严平稳顾名思义，是一种条件非常苛刻的平稳性，它要求序列随着时间的推移，其统计性质保持不变。对于任意的τ，其联合概率密度函数满足：
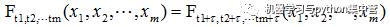
严平稳的条件只是理论上的存在，现实中用得比较多的是宽平稳的条件。
宽平稳也叫弱平稳或者二阶平稳（均值和方差平稳），它应满足：
常数均值
常数方差
常数自协方差
平稳性检验：观察法和单位根检验法
基于此，我写了一个名为test_stationarity的统计性检验模块，以便将某些统计检验结果更加直观的展现出来。
# -*- coding:utf-8 -*-
from statsmodels.tsa.stattools import adfuller
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 移动平均图
def draw_trend(timeSeries, size):
f = plt.figure(facecolor='white')
# 对size个数据进行移动平均
rol_mean = timeSeries.rolling(window=size).mean()
# 对size个数据进行加权移动平均
rol_weighted_mean = pd.ewma(timeSeries, span=size)
timeSeries.plot(color='blue', label='Original')
rolmean.plot(color='red', label='Rolling Mean')
rol_weighted_mean.plot(color='black', label='Weighted Rolling Mean')
plt.legend(loc='best')
plt.title('Rolling Mean')
plt.show()
def draw_ts(timeSeries):
f = plt.figure(facecolor='white')
timeSeries.plot(color='blue')
plt.show()
'''
Unit Root Test
The null hypothesis of the Augmented Dickey-Fuller is that there is a unit
root, with the alternative that there is no unit root. That is to say the
bigger the p-value the more reason we assert that there is a unit root
'''
def testStationarity(ts):
dftest = adfuller(ts)
# 对上述函数求得的值进行语义描述
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
return dfoutput
# 自相关和偏相关图，默认阶数为31阶
def draw_acf_pacf(ts, lags=31):
f = plt.figure(facecolor='white')
ax1 = f.add_subplot(211)
plot_acf(ts, lags=31, ax=ax1)
ax2 = f.add_subplot(212)
plot_pacf(ts, lags=31, ax=ax2)
plt.show()
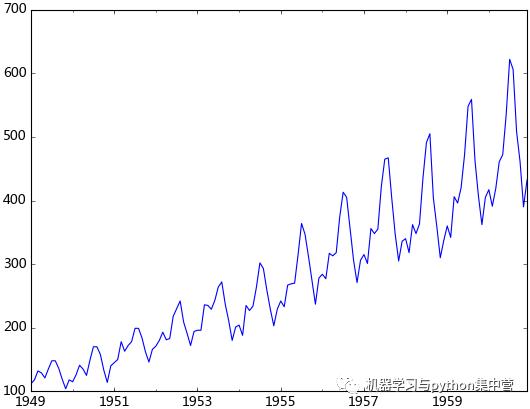
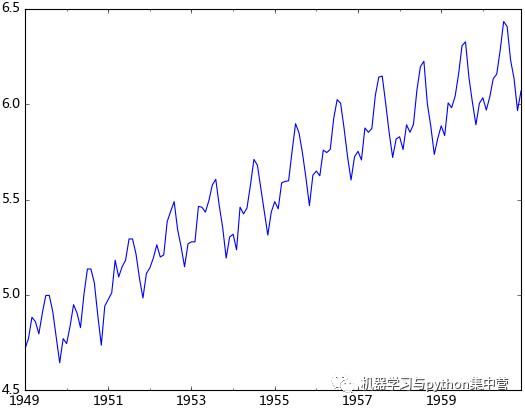
观察法，通俗的说就是通过观察序列的趋势图与相关图是否随着时间的变化呈现出某种规律。所谓的规律就是时间序列经常提到的周期性因素，现实中遇到得比较多的是线性周期成分，这类周期成分可以采用差分或者移动平均来解决，而对于非线性周期成分的处理相对比较复杂，需要采用某些分解的方法。下图为航空数据的线性图，可以明显的看出它具有年周期成分和长期趋势成分。平稳序列的自相关系数会快速衰减，下面的自相关图并不能体现出该特征，所以我们有理由相信该序列是不平稳的。
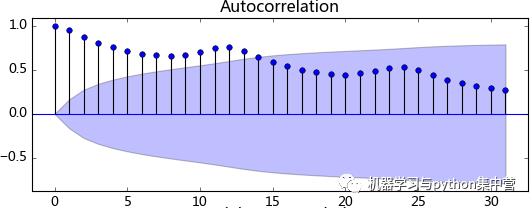
单位根检验：ADF是一种常用的单位根检验方法，他的原假设为序列具有单位根，即非平稳，对于一个平稳的时序数据，就需要在给定的置信水平上显著，拒绝原假设。ADF只是单位根检验的方法之一，如果想采用其他检验方法，可以安装第三方包arch，里面提供了更加全面的单位根检验方法，个人还是比较钟情ADF检验。以下为检验结果，其p值大于0.99，说明并不能拒绝原假设。
由前面的分析可知，该序列是不平稳的，然而平稳性是时间序列分析的前提条件，故我们需要对不平稳的序列进行处理将其转换成平稳的序列。
a. 对数变换
对数变换主要是为了减小数据的振动幅度，使其线性规律更加明显（我是这么理解的时间序列模型大部分都是线性的，为了尽量降低非线性的因素，需要对其进行预处理，也许我理解的不对）。对数变换相当于增加了一个惩罚机制，数据越大其惩罚越大，数据越小惩罚越小。这里强调一下，变换的序列需要满足大于0，小于0的数据不存在对数变换。
ts_log = np.log(ts)
test_stationarity.draw_ts(ts_log)
b. 平滑法
根据平滑技术的不同，平滑法具体分为移动平均法和指数平均法。
移动平均即利用一定时间间隔内的平均值作为某一期的估计值，而指数平均则是用变权的方法来计算均值。
test_stationarity.draw_trend(ts_log, 12)
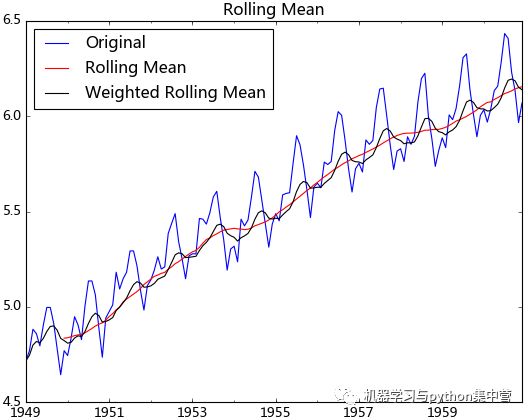
从上图可以发现窗口为12的移动平均能较好的剔除年周期性因素，而指数平均法是对周期内的数据进行了加权，能在一定程度上减小年周期因素，但并不能完全剔除，如要完全剔除可以进一步进行差分操作。
c. 差分
时间序列最常用来剔除周期性因素的方法当属差分了，它主要是对等周期间隔的数据进行线性求减。前面我们说过，ARIMA模型相对ARMA模型，仅多了差分操作，ARIMA模型几乎是所有时间序列软件都支持的，差分的实现与还原都非常方便。而statsmodel中，对差分的支持不是很好，它不支持高阶和多阶差分，为什么不支持，这里引用作者的说法：
作者大概的意思是说预测方法中并没有解决高于2阶的差分，有没有感觉很牵强，不过没关系，我们有pandas。我们可以先用pandas将序列差分好，然后在对差分好的序列进行ARIMA拟合，只不过这样后面会多了一步人工还原的工作。
diff_12 = ts_log.diff(12)
diff_12.dropna(inplace=True)
diff_12_1 = diff_12.diff(1)
diff_12_1.dropna(inplace=True)
test_stationarity.testStationarity(diff_12_1)
从上面的统计检验结果可以看出，经过12阶差分和1阶差分后，该序列满足平稳性的要求了。
d. 分解
所谓分解就是将时序数据分离成不同的成分。statsmodels使用的X-11分解过程，它主要将时序数据分离成长期趋势、季节趋势和随机成分。与其它统计软件一样，statsmodels也支持两类分解模型，加法模型和乘法模型，这里我只实现加法，乘法只需将model的参数设置为"multiplicative"即可。
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log, model="additive")
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
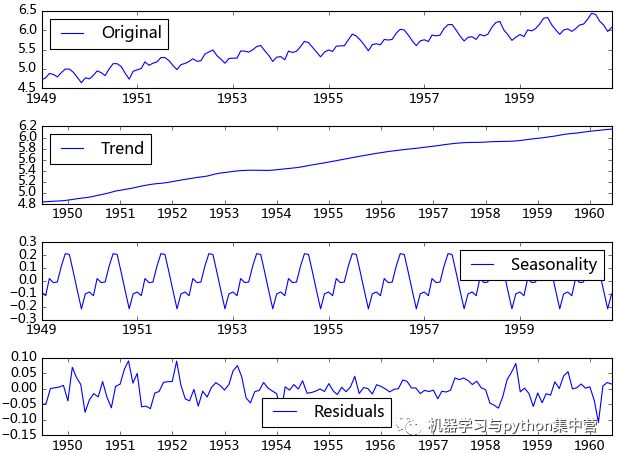
得到不同的分解成分后，就可以使用时间序列模型对各个成分进行拟合，当然也可以选择其他预测方法。我曾经用过小波对时序数据进行过分解，然后分别采用时间序列拟合，效果还不错。由于我对小波的理解不是很好，只能简单的调用接口，如果有谁对小波、傅里叶、卡尔曼理解得比较透，可以将时序数据进行更加准确的分解，由于分解后的时序数据避免了他们在建模时的交叉影响，所以我相信它将有助于预测准确性的提高。
在前面的分析可知，该序列具有明显的年周期与长期成分。对于年周期成分我们使用窗口为12的移动平进行处理，对于长期趋势成分我们采用1阶差分来进行处理。
rol_mean = ts_log.rolling(window=12).mean()
rol_mean.dropna(inplace=True)
ts_diff_1 = rol_mean.diff(1)
ts_diff_1.dropna(inplace=True)
test_stationarity.testStationarity(ts_diff_1)
观察其统计量发现该序列在置信水平为95%的区间下并不显著，我们对其进行再次一阶差分。再次差分后的序列其自相关具有快速衰减的特点，t统计量在99%的置信水平下是显著的，这里我不再做详细说明。
ts_diff_2 = ts_diff_1.diff(1)
ts_diff_2.dropna(inplace=True)
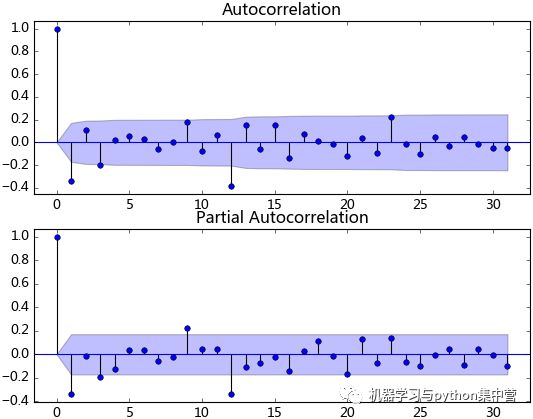
数据平稳后，需要对模型定阶，即确定p、q的阶数。观察上图，发现自相关和偏相系数都存在拖尾的特点，并且他们都具有明显的一阶相关性，所以我们设定p=1, q=1。下面就可以使用ARMA模型进行数据拟合了。这里我不使用ARIMA(ts_diff_1, order=(1, 1, 1))进行拟合，是因为含有差分操作时，预测结果还原老出问题，至今还没弄明白。
from statsmodels.tsa.arima_model import ARMA
model = ARMA(ts_diff_2, order=(1, 1))
result_arma = model.fit( disp=-1, method='css')
模型拟合完后，我们就可以对其进行预测了。由于ARMA拟合的是经过相关预处理后的数据，故其预测值需要通过相关逆变换进行还原。
predict_ts = result_arma.predict()
# 一阶差分还原
diff_shift_ts = ts_diff_1.shift(1)
diff_recover_1 = predict_ts.add(diff_shift_ts)
# 再次一阶差分还原
rol_shift_ts = rol_mean.shift(1)
diff_recover = diff_recover_1.add(rol_shift_ts)
# 移动平均还原
rol_sum = ts_log.rolling(window=11).sum()
rol_recover = diff_recover*12 - rol_sum.shift(1)
# 对数还原
log_recover = np.exp(rol_recover)
log_recover.dropna(inplace=True)
我们使用均方根误差（RMSE）来评估模型样本内拟合的好坏。利用该准则进行判别时，需要剔除“非预测”数据的影响。
ts = ts[log_recover.index] # 过滤没有预测的记录
plt.figure(facecolor='white')
log_recover.plot(color='blue', label='Predict')
ts.plot(color='red', label='Original')
plt.legend(loc='best')
plt.title('RMSE: %.4f'% np.sqrt(sum((log_recover-ts)**2)/ts.size))
plt.show()
观察上图的拟合效果，均方根误差为11.8828，感觉还过得去。
前面提到statsmodels里面的ARIMA模块不支持高阶差分，我们的做法是将差分分离出来，但是这样会多了一步人工还原的操作。基于上述问题，我将差分过程进行了封装，使序列能按照指定的差分列表依次进行差分，并相应的构造了一个还原的方法，实现差分序列的自动还原。
# 差分操作
def diff_ts(ts, d):
global shift_ts_list
# 动态预测第二日的值时所需要的差分序列
global last_data_shift_list
shift_ts_list = []
last_data_shift_list = []
tmp_ts = ts
for i in d:
last_data_shift_list.append(tmp_ts[-i])
print last_data_shift_list
shift_ts = tmp_ts.shift(i)
shift_ts_list.append(shift_ts)
tmp_ts = tmp_ts - shift_ts
tmp_ts.dropna(inplace=True)
return tmp_ts
# 还原操作
def predict_diff_recover(predict_value, d):
if isinstance(predict_value, float):
tmp_data = predict_value
for i in range(len(d)):
tmp_data = tmp_data + last_data_shift_list[-i-1]
elif isinstance(predict_value, np.ndarray):
tmp_data = predict_value[0]
for i in range(len(d)):
tmp_data = tmp_data + last_data_shift_list[-i-1]
else:
tmp_data = predict_value
for i in range(len(d)):
try:
tmp_data = tmp_data.add(shift_ts_list[-i-1])
except:
raise ValueError('What you input is not pd.Series type!')
tmp_data.dropna(inplace=True)
return tmp_data
现在我们直接使用差分的方法进行数据处理，并以同样的过程进行数据预测与还原。
diffed_ts = diff_ts(ts_log, d=[12, 1])
model = arima_model(diffed_ts)
model.certain_model(1, 1)
predict_ts = model.properModel.predict()
diff_recover_ts = predict_diff_recover(predict_ts, d=[12, 1])
log_recover = np.exp(diff_recover_ts)
是不是发现这里的预测结果和上一篇的使用12阶移动平均的预测结果一模一样。这是因为12阶移动平均加上一阶差分与直接12阶差分是等价的关系，后者是前者数值的12倍，这个应该不难推导。
对于个数不多的时序数据，我们可以通过观察自相关图和偏相关图来进行模型识别，倘若我们要分析的时序数据量较多，例如要预测每只股票的走势，我们就不可能逐个去调参了。这时我们可以依据BIC准则识别模型的p, q值，通常认为BIC值越小的模型相对更优。这里我简单介绍一下BIC准则，它综合考虑了残差大小和自变量的个数，残差越小BIC值越小，自变量个数越多BIC值越大。个人觉得BIC准则就是对模型过拟合设定了一个标准（过拟合这东西应该以辩证的眼光看待）。
def proper_model(data_ts, maxLag):
init_bic = sys.maxint
init_p = 0
init_q = 0
init_properModel = None
for p in np.arange(maxLag):
for q in np.arange(maxLag):
model = ARMA(data_ts, order=(p, q))
try:
results_ARMA = model.fit(disp=-1, method='css')
except:
continue
bic = results_ARMA.bic
if bic < init_bic:
init_p = p
init_q = q
init_properModel = results_ARMA
init_bic = bic
return init_bic, init_p, init_q, init_properModel
相对最优参数识别结果：BIC: -1090.44209358 p: 0 q: 1 ， RMSE:11.8817198331。我们发现模型自动识别的参数要比我手动选取的参数更优。
所谓滚动预测是指通过添加最新的数据预测第二天的值。对于一个稳定的预测模型，不需要每天都去拟合，我们可以给他设定一个阀值，例如每周拟合一次，该期间只需通过添加最新的数据实现滚动预测即可。基于此我编写了一个名为arima_model的类，主要包含模型自动识别方法，滚动预测的功能，详细代码可以查看附录。数据的动态添加：
from dateutil.relativedelta import relativedelta
def _add_new_data(ts, dat, type='day'):
if type == 'day':
new_index = ts.index[-1] + relativedelta(days=1)
elif type == 'month':
new_index = ts.index[-1] + relativedelta(months=1)
ts[new_index] = dat
def add_today_data(model, ts, data, d, type='day'):
_add_new_data(ts, data, type) # 为原始序列添加数据
# 为滞后序列添加新值
d_ts = diff_ts(ts, d)
model.add_today_data(d_ts[-1], type)
def forecast_next_day_data(model, type='day'):
if model == None:
raise ValueError('No model fit before')
fc = model.forecast_next_day_value(type)
return predict_diff_recover(fc, [12, 1])
现在我们就可以使用滚动预测的方法向外预测了，取1957年之前的数据作为训练数据，其后的数据作为测试，并设定模型每第七天就会重新拟合一次。这里的diffed_ts对象会随着add_today_data方法自动添加数据，这是由于它与add_today_data方法中的d_ts指向的同一对象，该对象会动态的添加数据。
ts_train = ts_log[:'1956-12']
ts_test = ts_log['1957-1':]
diffed_ts = diff_ts(ts_train, [12, 1])
forecast_list = []
for i, dta in enumerate(ts_test):
if i%7 == 0:
model = arima_model(diffed_ts)
model.certain_model(1, 1)
forecast_data = forecast_next_day_data(model, type='month')
forecast_list.append(forecast_data)
add_today_data(model, ts_train, dta, [12, 1], type='month')
predict_ts = pd.Series(data=forecast_list, index=ts['1957-1':].index)
log_recover = np.exp(predict_ts)
original_ts = ts['1957-1':]
动态预测的均方根误差为：14.6479，与前面样本内拟合的均方根误差相差不大，说明模型并没有过拟合，并且整体预测效果都较好。
在进行动态预测时，我们不希望将整个模型一直在内存中运行，而是希望有新的数据到来时才启动该模型。这时我们就应该把整个模型从内存导出到硬盘中，而序列化正好能满足该要求。序列化最常用的就是使用json模块了，但是它是时间对象支持得不是很好，有人对json模块进行了拓展以使得支持时间对象，这里我们不采用该方法，我们使用pickle模块，它和json的接口基本相同，有兴趣的可以去查看一下。我在实际应用中是采用的面向对象的编程，它的序列化主要是将类的属性序列化即可，而在面向过程的编程中，模型序列化需要将需要序列化的对象公有化，这样会使得对前面函数的参数改动较大，我不在详细阐述该过程。
04
总结
与其它统计语言相比，python在统计分析这块还显得不那么“专业”。随着numpy、pandas、scipy、sklearn、gensim、statsmodels等包的推动，我相信也祝愿python在数据分析这块越来越好。与SAS和R相比，python的时间序列模块还不是很成熟，我这里仅起到抛砖引玉的作用，希望各位能人志士能贡献自己的力量，使其更加完善。实际应用中我全是面向过程来编写的，为了阐述方便，我用面向过程重新罗列了一遍，实在感觉很不方便。原本打算分三篇来写的，还有一部分实际应用的部分，不打算再写了，还请大家原谅。实际应用主要是具体问题具体分析，这当中第一步就是要查询问题，这步花的时间往往会比较多，然后再是解决问题。以我前面项目遇到的问题为例，当时遇到了以下几个典型的问题：1.周期长度不恒定的周期成分，例如每月的1号具有周期性，但每月1号与1号之间的时间间隔是不相等的；2.含有缺失值以及含有记录为0的情况无法进行对数变换；3.节假日的影响等等。
以上是关于python实践——时间序列分析建模理论及代码实现的主要内容，如果未能解决你的问题，请参考以下文章