常微分方程在推荐系统中的应用
Posted 推荐系统与数据挖掘
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了常微分方程在推荐系统中的应用相关的知识,希望对你有一定的参考价值。
1 摘要
本文最大的贡献就是创新性的把离散的隐藏状态转变为连续的状态,可以很好的捕获动态的趋势。
1.1相关工作
用微分方程的视角来看待和理解神经网络是一种新的视角,该观点最早出现在2016年鄂维南院士的一篇proposal里:A Proposal on Machine Learning viaDynamical Systems.。
在Neural 2018中,来自多伦多大学的陈天琦,提出的Neural ODE获得了NeurIPS的最佳论文奖。在这篇文章中,作者创新性的把离散的隐藏状态转变为连续的状态。传统的神经网络会使用一系列的离散隐藏层,而这篇文章利用一个神经网络将隐藏状态的微分进行了参数化。这一神经网络的输出由一个黑箱的微分方程求解器进行计算求解。像这样的连续深度神经网络具有常量的内存消耗,可以根据每一个输入自适应地调整求值策略,并可以显式地进行数值精度和求解速度之间的交换。
在AAAI 2020中,将神经常微分方程应用到了推荐系统中,解决了用户兴趣随着时间动态变化的问题。
本篇论文着重讲常微分方程在推荐系统中的一个应用:DTS模型,并且重点讲微分方程。该模型已在工业界中尝试应用。
1.2常微分方程的数值解法
1.2.1常微分方程引例
对于给定一个初值(变化过程开始的地方),我们可以确定一条曲线,它描述了状态y随着过程x的变化。
图1-1 常微分方程引例
1.2.2常微分方程的解法
在适当的形式下,常微分方程可以解析求解,但通常是数值求解。求微分方程最简单古老的古方法就是欧拉方法,其核心思想是用切线逐步逼近函数,公式如下所示。

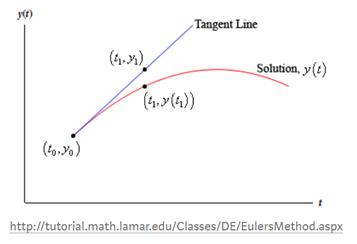
图1-2 欧拉方法
1.3 ResNets和RNNs与微分方程的联系
ResNet:,其中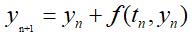 是输入,
是输入,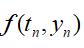 是该层自身的输出,显然这是一个微分方程,特定于时间间隔为1的情况。
是该层自身的输出,显然这是一个微分方程,特定于时间间隔为1的情况。
对于RNNs有隐藏状态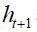 和
和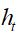 ,
,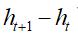 可以解释为
可以解释为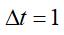 的离散化导数
的离散化导数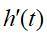 ,当
,当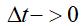 时有
时有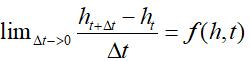 。微分方程
。微分方程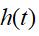 的解可以由ODE求解器得到。其中这个求解器可以是我们数值分析课程中学的方法,比如龙格-库塔方法。
的解可以由ODE求解器得到。其中这个求解器可以是我们数值分析课程中学的方法,比如龙格-库塔方法。
2 Deep Time-Stream Framework forClick-Through Rate Prediction by TrackingInterest Evolution(DTS模型)
2.1摘要
人们提出了深度学习模型来学习用户整体兴趣的表示,但忽略了兴趣可能会随着时间动态变化的事实。我们认为在CTR模型中考虑连续时间信息,从丰富的历史行为中跟踪用户的兴趣趋势是必要的。
因此,作者提出了一种新的深度时间流框架(DTS),它将time-stream信息引入到CTR模型中。具体来说,DTS通过参数化用户潜在兴趣状态对时间的导数,利用ODE对用户潜在兴趣的演化进行建模,使得ODE的求解描述了用户兴趣的动态演化。此外,DTS具有通过点击时间戳统一用户历史行为(点击了什么)和目标项目(将点击什么)在time-stream上的能力,从而可以对给定的下一次做出相应的推断,提供更精确的CTR预测。
2.2模型介绍
2.2.1模型
我们首先将CTR形式化为一个二分类问题。最小化下列函数:
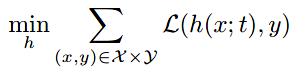
DTS模型由BaseModel和Time-Stream 模块组成,即DTS = BaseModel +Time-Stream Module。一般的base model是embedding-pooling-MLP,先对输入进行embedding提取信息,再喂到池化层提取主要信息,最后送入多层感知机中得到最后的输入。
2.2.2 Time-Stream 模块
用户的兴趣是随时间变化的,而不是静态的。BaseModel通过对所单击的项特性进行池化操作来获得用户感兴趣的表示向量,但忽略时间信息。动态模式的缺乏限制了用户行为特性的能力,而用户点击的项目是用户在相应时间内兴趣的表达,因此用户行为特性是用户兴趣建模的关键。对于BaseModel来说,由于缺乏对连续模式的建模能力,导致无法准确地对用户动态兴趣进行建模。
是否有一种优雅的方式来表示用户的实时兴趣并对动态兴趣演化模式进行建模?连续时间演化的本质启发作者设计一种新的方法,称为time-stream框架ODE用于建立动态兴趣跟踪模型。
ODE可以是RNNs的一般形式,而RNNs可以看作是连续ODE的离散化。连续的ODE方法具有灵活的计算能力,可以自适应地选择神经网络的长度。此外,我们还可以使用先进的数值方法进行训练,如多网格法或并行射击法。下图详细说明了Time-Stream Module。
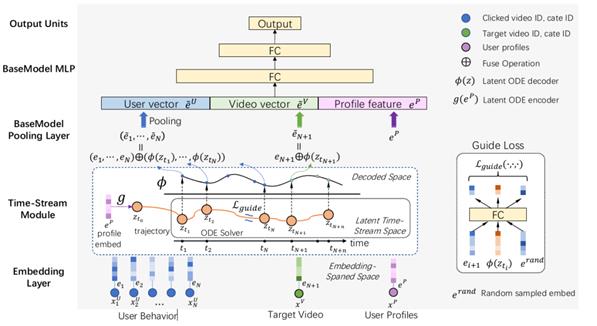
图2-1 模型示意图
2.2.3 初值的获取
因为相似的人具有相似的兴趣演化模式,我们通过构造一个映射g将user profile embedding 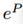 变换到一个潜语义time-stream 空间来得到初值
变换到一个潜语义time-stream 空间来得到初值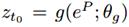 。有如下式子:
。有如下式子:
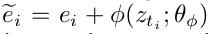
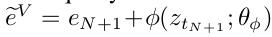
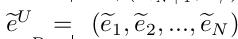
另一方面,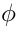 是将潜语义time-stream 特征zti转换到video embedding-spanedspace。
是将潜语义time-stream 特征zti转换到video embedding-spanedspace。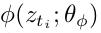 是对用户行为的补充,带有额外的行为进化模式信息。
是对用户行为的补充,带有额外的行为进化模式信息。
2.2.4 微分方程的定义
简单形式:
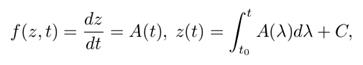
A是一个控制函数,C是一个常数在初始状态下可以解出来。当
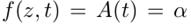
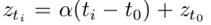
从中可以看出,f单调的轨迹模仿了用户兴趣的特征:主要受近期兴趣的影响,所以应该减少早期兴趣的影响,增加用户近期行为的影响。这种特殊情况非常简单,但在实验中却表现出惊人的性能。
复杂的形式:
上述简单的f形式无法表达用户多样的时间序列模式。为了克服这一局限性,另一种方法是利用神经网络对动力学f的导数进行参数化,大大提高了模型的表达能力。本文使用的是具有sigmoid激活单元的两层神经网络:
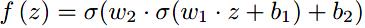
实验结果:
以上是关于常微分方程在推荐系统中的应用的主要内容,如果未能解决你的问题,请参考以下文章