推荐系统 | 一文带你了解协同过滤的前世今生

Posted 2021-05-01 小小挖掘机

导读

协同过滤：在推荐领域中，让人耳熟能详、影响最大、应用最广泛的模型莫过于协同过滤。2003年，Amazon发表的论文[1]让协同过滤成为今后很长时间的研究热点和业界主流的推荐模型。

什么是协同过滤

协同过滤是 基于用户行为设计的推荐算法，具体来说，是 通过群体的行为来找到某种相似性（用户之间的相似性或者物品之间的相似性），通过相似性来为用户做决策和推荐。从字面上理解，协同过滤包括协同和过滤两个操作。协同就是汇集所有用户的反馈、评价等（与网站不断进行互动。而过滤，通过协同得到的信息，从海量物品进行过滤，筛选出用户感兴趣的物品。

协同过滤的分类

关于协同过滤方法的分类众说不一，这里结合项亮《推荐系统实战》 [2]一书中的分类，将其分为：

1. 传统的协同过滤方法

• 基于邻域的方法

            基于用户的协同过滤方法

            基于物品的协同过滤方法

• 隐语义模型

            矩阵分解

• 基于图的随机游走方法

      PageRank

2. 基于深度学习的协同过滤方法

• 基于表示学习的模型

• 基于匹配方法学习的模型

传统的协同过滤算法

基于邻域的方法

基于邻域的方法 根据计算用户或物品的相似性的不同又细分为两种：基于用户的协同过滤（User CF）和基于物品的协同过滤（Item CF）。

相似度

在基于邻域的方法中，计算用户或物品的相似度至关重要。这里我们假设两个用户（物品）向量为 和 ，两个向量之间的相似度计算方法主要有如下几种：

1. Jaccard系数：用于计算两个集合之间的相似度，比较适合隐式反馈类型的用户行为。

2. Cosine相似度：用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似。

3. Pearson相关性系数：是衡量向量相似度的一种方法。输出范围为[-1, +1]， 0代表无相关性，负值为负相关，正值为正相关。

基于用户的协同过滤

基于用户的协同过滤算法的简单定义：在一个在线个性化推荐系统中，当一个用户需要个性化推荐时，可以先找到和他有相似兴趣的其他用户，然后把那些用户喜欢的、而当前用户没有听说过的物品推荐给他。简而言之，就是去找到志同道合（相似）的用户，这些用户可以互相补充各自的评分。

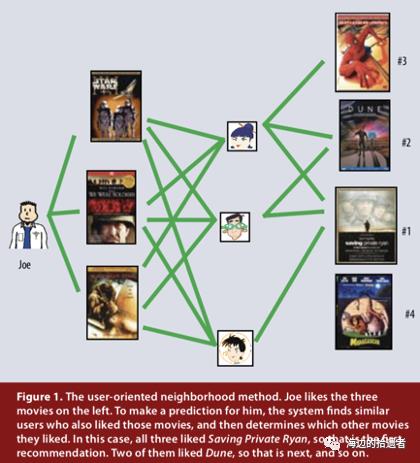
基于用户的协同过滤符合人们直觉上的思想，但是也存在以下缺陷：

（1）当用户数远大于物品数，用户相似度矩阵的开销会特别大。

（2）当用户行为过于稀疏时，找到相似用户的准确度是特别低的。

（3）解释性不强。

基于物品的协同过滤

由于基于用户的协同过滤的缺陷，当时Amazon采用了基于物品的协同过滤方法来实现最初的推荐系统。基于物品的协同过滤算法并 不利用物品的内容属性计算物品之间的相似度，它主要通过分析用户的行为记录计算物品之间的相似度。

该算法认为：物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。

基于物品的协同过滤的解释性强（讨论的是物品的相似性），但也存在着一些缺陷：

（1）当物品数远大于用户数，物品相似度矩阵的开销会特别大。

（2）当有新物品时，没有办法在不离线更新物品相似度表的情况下将新物品推荐给用户；

总结

关于基于用户的协同过滤和基于物品的协同过滤出的选择需要对当前背景进行分析判断。基于用户的协同过滤适合时效性较强，用户的个性化兴趣不太明显的领域，如新闻领域；而基于物品的协同过滤适合兴趣变化较为稳定的应用，比如电商场景、视频推荐等。

对于基于邻近的方法，虽然其解释性较强，但是它并不具有较强的泛化能力。处理稀疏向量的能力弱。因此为了解决这个问题，矩阵分解技术被提出。

隐语义模型

矩阵分解

矩阵分解是隐语义模型中最成功的方法，2006年，Netflix举办的著名推荐算法竞赛Netflix Prize Challenge中，矩阵分解技术大放光彩，因此我们直接对矩阵分解进行讨论。

矩阵分解引入了一个隐向量（latent vector）的概念，通过从物品评分模式中推断出的隐向量来表征物品和用户。隐向量，类似于NLP中的Word2vec技术，也就是后来深度学习中的Embedding向量。隐向量的不同的因子可能表示不同的具体含义，对于电影来说，发现的因素可能会衡量明显的维度，例如喜剧与戏剧，动作量或对儿童的定向；不太明确的尺寸，例如角色发展的深度或古怪程度；亦或者是完全无法解释的尺寸。对于用户来说，每个因素都会衡量用户对在相应电影的喜欢程度。

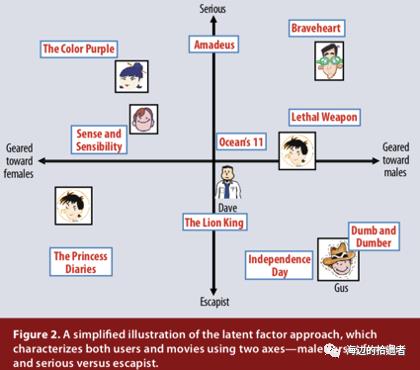
适用于推荐系统的矩阵分解的主要方法有两种：奇异值分解（Singular Value Decomposition）和梯度下降（Gradient Descent）。

• 奇异值分解（SVD）

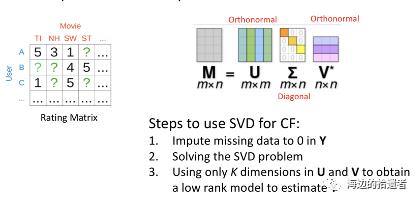
以上等于求解一个最优化问题：

但使用SVD方法存在一些缺陷：

1. 奇异值分解要求原始的共现矩阵是稠密的。然而现实中用户-物品矩阵非常稀疏，这与奇异值分解的应用条件相悖。如果应用，就必须对确实元素进行填充，如填充0。这样缺失的数据和所观测的数据具有相同的权重。
2. 无法进行正则化，容易过拟合。
3. 计算复杂度高 。

因此传统的奇异值分解也并不适合大规模稀疏矩阵的矩阵分解问题。因此梯度下降法成为了进行矩阵分解的主要方法。

• 梯度下降法

梯度下降法通常是用来求解无约束最优化问题的一种最常用方法，是一种迭代算法。

最基础的模型为：

其中 为用户隐向量（user latent vector）， 为物品隐向量（item latent vector）。

损失函数为：

其中 为正则化参数。

MF主要分为两步：

1. 将用户和物品都表示为隐向量。
2. 使用内积（inner product）作为用户和物品之间的交互函数，结果代表为用户对物品的偏好程度。

然后使用梯度下降法对其进行优化，同时可以加入正则化来降低模型的过拟合。

• SVD++

2008年，Korean等人[3]提出的SVD++模型。SVD++融合了MF和FISM[4]的优势，直接将Implicit数据反馈到模型中，优化了对用户的表示：

其中 表示用户和物品的偏置， 分别表示用户、物品的隐向量， 表示用户 对所有物品的隐式偏好。

• 加入额外信息

2009年，koren对矩阵分解模型进行总的概括和扩展[5]，除了基础的模型，主要加入了一些额外信息：

（1）添加偏置（adding biaes）：虽然基本的矩阵分解可以捕获用户和物品之间的交互，但是，观察到的许多评分变化是由于与用户或物品相关的影响（称为偏差）所致，而与任何交互无关。

因此单纯用内积的交互来解释一个评分值是比较粗糙的。因此，使用偏置来解释用户/物品的自身影响：

其中 被定义为总平均评分（例如单个用户对所有电影的平均评分），参数 和 分别表示物品和用户的偏置，将偏置加入最终的评分中：

评分被分解为四项：总平均得分，物品偏置，用户偏置和物品用户的交互。

（2）额外的输入源（additionaL input sources）：推荐系统总会面临一个冷启动问题，一个缓解这个问题的方案是添加额外的用户信息源。推荐系统可以使用隐式反馈来深入了解用户的偏好。实际上，无论用户是否愿意提供明确的评分，他们都可以收集行为信息。零售商除了可以提供客户的评价外，还可以使用其客户的购买或浏览历史记录来了解其趋势。

简单起见，定义一个 来表示用户隐式偏好的物品集。对于物品 关联一个向量 (等于对每一个物品的隐式偏好做一个one-hot编码）。因此，一个用户的偏爱对于在 中的物品来说可以形容为一个向量：

归一化后，

另一个信息源是用户属性，定义一个布尔属性 来表示用户 相关的信息，如性别、年龄、组群、所在地的邮编、收入水平等，对于每一个属性可以用一个向量表示， ，一个用户的所有属性表示为：

矩阵分解模型整合输入源，最后的评分形式为：

（3）时间的动态性（temporaL dynamics）：随着新选择的出现，物品的感知度和受欢迎度会不断变化。同样，用户的喜好也在不断发展，导致他们重新定义了品味。矩阵分解方法非常适合于对时间效应进行建模，从而可以显着提高准确性。将评分分解为不同的项可以使系统分别处理不同的时间方面。

一个评分项中随着时间的改变发生变化的有：物品偏置 ，用户偏置 以及用户偏好 。最终评分形式可以变为：

• 矩阵分解技术总结

矩阵分解有很多优点：

1. 泛化能力强。在一定程度上解决了数据稀疏问题。
2. 空间复杂度低。不需要存储用户相似或物品相似矩阵，只需存储用户和物品的隐向量。空间复杂度由 降低到 级别。
3. 更好的扩展性和灵活性。矩阵分解最后得到用户和物品隐向量，这其实与深度学习中的Embedding思想不谋而合，因此矩阵分解的觉果非常便于与其他特征进行组合和拼接。

但矩阵分解也存在一定的局限性。总的来说应该是整个协同过滤模型的局限性，无法加入用户、物品属性、上下文特征等边信息，这是的丧失了很多有效信息，无法进行有效的推荐。

基于图的随机游走方法

PageRank

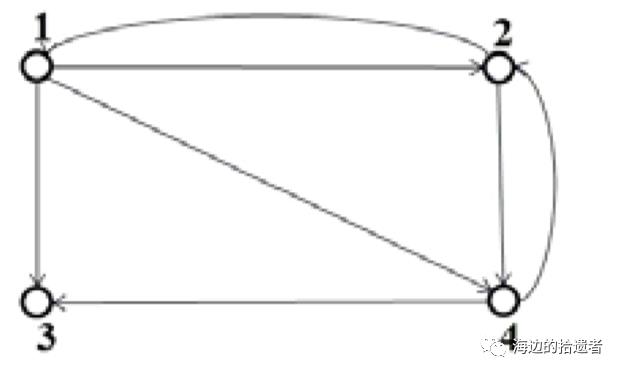
• 二部图

在推荐系统中，用户-商品数据可以转换成二部图的存储形式，其中，在转化后的用户-商品二部图中，两个子集V1 和V2 分别为用户节点的集合和商品节点的集合。常见二部图如下：

例如有一个用户-商品矩阵，将其转换为二部图。

其中，未打分的地方“-”用0表示。

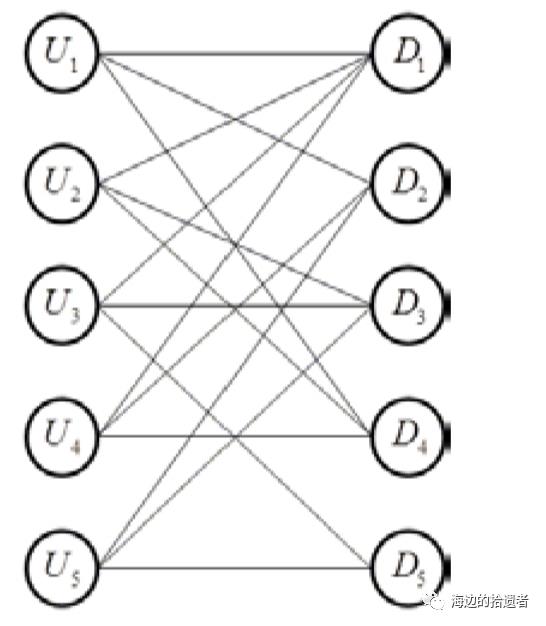
在推荐系统中，其最终的目的是为用户Ui 推荐相关的商品，此时，对于用户Ui ，需要计算商品列表{D1 ，D2 ，...，D5 }中的商品对其重要性程度，并根据重要性程度生成最终的推荐列表。PageRank算法是用于处理图上的重要性排名的算法。

• PageRank算法概念

PageRank算法，即网页排名算法，是由佩奇和布林在1997年提出来的链接分析算法。PageRank是用来标识网页的等级、重 要性的一种方法，是衡量一个网页的重要指标。

网页的链接分析可以抽象成图模型，如下所示。

对于某个网页的PageRank的计算是基于以下两个假设:

数量假设。在 Web 图模型中，如果一个页面节点接收到的其他网页指向的链接数量越多，那么这个页面就越重要。即: 链接到网页 A 的链接数越多，网页A越重要。

质量假设。指向页面 A 的入链的质量不同，质量高的页面会通过链接向其他的页面传递更多的权重，所以越是质量高的 页面指向页面 A，则页面 A 越重要。即:链接到网页A的原网页越重要，则网页A也会越重要。

PageRank算法很好地 组合了这两个假设，使得对网页的重要性评价变得更加准确。

• 计算算法

利用PageRank算法计算节点的过程分别为：1.将有向图转换成图的邻接矩阵M;2.计算出链接概率矩阵;3.计算概率转移矩阵;4.修改概率转移矩阵;5.迭代求解PageRank值。

对于上述的PageRank算法，其计算公式可以表示为:

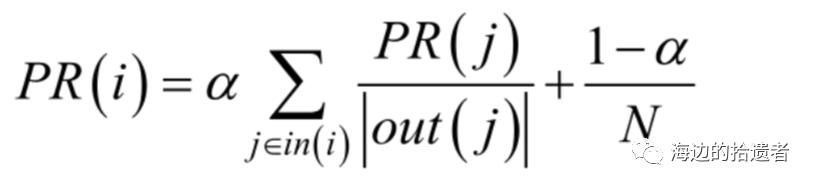
其中，PR(i)表示的是图中i节点的PageRank值，α 表示转移概率(通常取0.85)，N表示的是网页的总数，in(i)表示的是指向网页i的网 页集合，out(j)表示的是网页 j指向的网页集合。

基于深度学习的协同过滤

深度学习匹配模型可以分为两类：基于表示学习的模型和基于匹配方法学习的的模型。基于深度学习的协同过滤方法也可以按此进行划分。

基于表示学习的模型

结构如下：

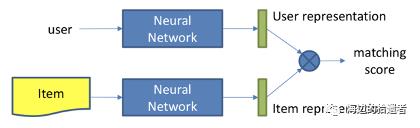
用户和物品分别通过神经网络生成各自的Embedding向量，即表示向量。将其作为中间产物，然后再通过内积等交互函数得到匹配分数，进行排序推荐。

【注】：Embedding向量学习与得到匹配分数的学习是分开的。

AutoRec

AutoRec模型 [5]利用协同过滤中的共现矩阵，完成物品向量或者用户向量的自编码。再利用自编码的结果得到用户对物品的评分，完成推荐。

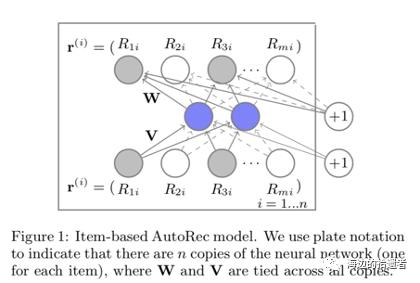
DeepMF

DeepMF模型 [6]是一种具有神经网络架构的矩阵分解模型。首先，构造一个具有明确评分和非偏好隐式反馈的用户物品共现矩阵。以此矩阵作为输入，提出了一种深度结构学习体系结构，以学习用于用户和物品表示的通用低维空间。其次，作者基于二元交叉熵设计了一个新的损失函数，以实现更好的优化。

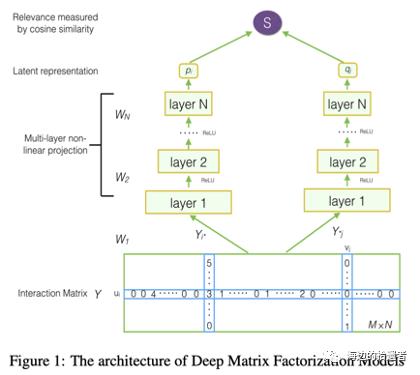
基于匹配方法学习的模型

基于匹配方法学习的深度推荐模型结构如下：

是一个端到端的模型。

NCF

NCF（Neural collaborative filtering）模型 [7]是一个端到端的模型。模型使用Embedding层来学习用户和物品的低维向量表示，并且用多层神经网络代替了矩阵分解模型中的内积操作，提高了特征的交叉能力。并且NeuralCF模型将通用的矩阵分解模型（加入了非线性的激活函数）与基于MLP协同过滤模型相结合来提高模型的性能。

ONCF

ONCF（Outer product-based neural collaborative filtering）模型 [8]是在NCF的基础上在用户embedding和物品的embedding的交互采用外积操作替换了原来的拼接操作。

总结

协同过滤只依赖于过去的用户行为，从最传统的基于邻近的方法，推进到基于矩阵分解的协同过滤。然后进入深度学习时代，协同过滤与深度学习紧密的结合，提高了传统的协同过滤模型的特征交叉能力，通过特征非线性的组合来优化模型。但是基于深度学习的协同过滤模型的基本原理还是经典的协同过滤的思路。

参考文献

[1]: Linden G, Smith B, York J. Amazon. com recommendations: Item-to-item collaborative filtering[J]. IEEE Internet computing, 2003, 7(1): 76-80. 

[2]: 项亮.推荐系统实战[M].北京：人民邮电出版社，2012.

[3]: Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model[C]//Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. 2008: 426-434. 

[4]: Kabbur S, Ning X, Karypis G. Fism: factored item similarity models for top-n recommender systems[C]//Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. 2013: 659-667. 

[5]: Sedhain S, Menon A K, Sanner S, et al. Autorec: Autoencoders meet collaborative filtering[C]//Proceedings of the 24th international conference on World Wide Web. 2015: 111-112. 

[6]: Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30-37. 

[7]: He X, Liao L, Zhang H, et al. Neural collaborative filtering[C]//Proceedings of the 26th international conference on world wide web. 2017: 173-182. 

[8]: He X, Du X, Wang X, et al. Outer product-based neural collaborative filtering[J]. arXiv preprint arXiv:1808.03912, 2018.

看完本文的你，对协同过滤技术有什么新的看法呢，欢迎交流～