推荐系统｜局部排序-全局融合的top-n推荐
Posted MINS
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了推荐系统｜局部排序-全局融合的top-n推荐相关的知识，希望对你有一定的参考价值。
本次为大家带来一篇推荐算法论文的导读，该论文已被Applied Soft Computing（IF: 5.472）在线刊发（Volume 96, November 2020）。
题目：Local Ranking and Global Fusion for Personalized Recommendation
DOI: https://doi.org/10.1016/j.asoc.2020.10663601
论文整体介绍
当前大多数的top-n推荐算法都基于全部用户-物品的行为数据来学习一个推荐列表，这里隐含着一个假设是所有的用户（或物品）都处于同一个特征空间。我们认为这种假设是限制推荐性能进一步提升的因素之一，因为在全局空间下学到的特征粒度比较粗，而在这种全局空间下学到的推荐列表可能被用户兴趣的一些显著部分所主导。
这篇文章提出了一种新颖的局部排序-全局融合框架LRGF，它允许使用多个更细粒度的局部特征空间来进行排序学习。一方面，LRGF希望不同的局部特征空间能够捕获用户兴趣（或物品属性）的不同方面，因为每个用户和物品都能被分配进多个特性不同的子群；另一方面，因为不同局部空间学到的特征有不同的特性，LRGF直接从不同的局部空间融合所生成的局部列表，而不是融合局部的预测分数。
LRGF框架包含两个部分：（1）局部排序（2）全局融合。在（1）局部排序中，首先将用户和物品划分成不同的子群，每个子群都是由最相关的用户和物品组成的。在每个子群中，本文又进一步提出了考虑成对差距的BPR算法来进行局部的排序学习；在（2）全局融合中，LRGF框架采用了一种决策融合方式直接融合各个子群生成的局部列表，融合既考虑局部列表的顺序，也同时考虑了各个子群的特性。
02
算法介绍
LRGF框架包含局部排序和全局融合两个部分，其中在局部排序中，LRGF提出了一种新的pairwise gap-aware BPR的成对排序算法，这种排序算法可以应用在一个更通用的排序任务中。下面将先介绍这种Pairwise gap-aware BPR的排序算法，再介绍LRGF框架的具体细节。
BPR算法是一种广泛应用的成对排序算法，与预测一个物品的打分不同，它预测的是一对物品之间的成对偏好。然而，对不同的物品对，BPR算法不能区分出他们之间偏好关系的相对强弱，而这种相对强弱关系是可以从用户对物品的评分数据中抽取出来的。
如上图所示，对于一个用户看过的样本，用户对其的打分反应了用户对其的热爱程度；对于一个用户没看过的样本，它可能是用户没注意到它，也可能是用户不喜欢它。因此不同物品对之间的偏好差距是不一样的。
对于样本(u,i,j), 定义积极度描述样本i，它等于用户对其的打分
，定义消极度NL描述样本j，因为j是用户没有看过的样本，因此利用j被别的用户打分情况去预估其消极度：
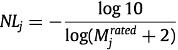
从而可以计算出训练样本(u,i,j)中物品对的偏好差距为：
最终该排序模型的损失函数为
完整的LRGF框架是由3步骤完成的：（1）构建用户-物品子群 （2）在子群生成排序列表 （3）融合局部列表生产全局列表。下图是算法的完整框架。
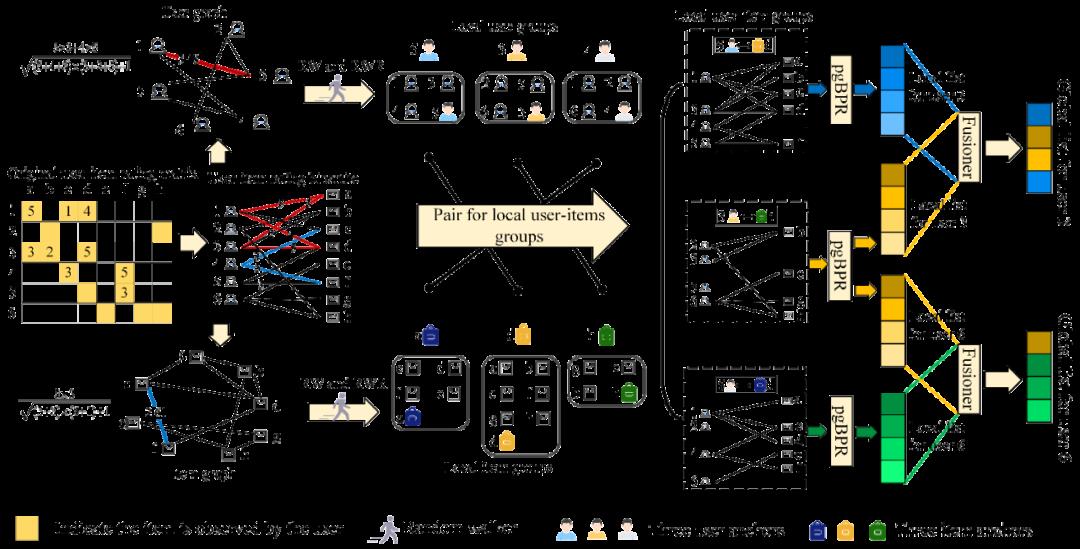
（1) 用户-物品子群构建
步骤一：图转换
基于用户-物品的评分数据，可以得到一个用户-物品二分图：若用户对物品进行过打分，则该用户和物品节点间将存在一条无向的连边，连边的权重是评分的分值。接下来将这个二分图转换成一个用户图和一个物品图。
具体规则为：如果两个用户给相同的物品打过分，则这两个用户之间存在一条连边，物品同理。具体转换公式如下：
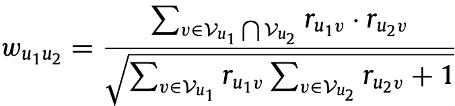
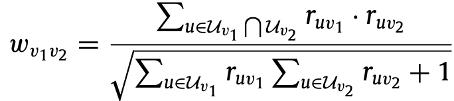
步骤二：锚点选择
接下来分别在用户图和物品图上进行随机游走，选择一批用户锚点和物品锚点。这里以用户图为例介绍具体过程：
对用户图的邻接矩阵进行列归一化，得到其转移概率矩阵
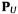。随机初始化每一个用户节点的概率，然后在用户图上进行随机游走，直至收敛:
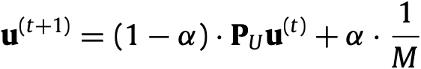
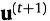表示t轮迭代时的全体用户的节点概率向量。根据每个节点收敛时的概率值，选择收敛概率最大的A个用户作为用户锚点，用
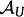表示这A个用户锚点的集合；物品同理可以按照此方法获得A个物品锚点，用
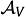表示这A个物品锚点的集合。
步骤三：子群构建
以构建用户子群为例。对于第二步所确定的每个用户锚点，以其为重启动节点，在用户图上进行带重启动的随机游走：
游走收敛以后，每个用户节点都会得到自身的收敛概率，该值反映了它与当前锚点的近似关系；对于每个用户，将其分配给使它收敛最大的
个用户锚点；从而所有分配给锚点
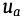的用户组成了用户子群 
。对于每个物品锚点，采用类似的过程游走，可以得到每一个物品子群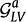 
。
最后，将A个用户锚点和A个物品锚点进行随机匹配，组成A个用户-物品锚点对。对于锚点对
。它相应的用户子群
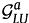和物品子群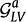形成了用户-物品子群
。
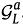（2) 局部排序
接下来，在每个子群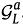里，采用提出的pgBPR算法进行排序学习。其中每个物品对中，用户看过的物品的积极度仍然等于其打分；而对于用户没看过的物品j，在计算他的消极度时，应该考虑它所属的子群数据分布的特性：
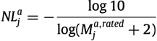
从而对于三元组(u,i,j)在子群a 中，i 和 j 之间的偏好差距为
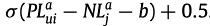
在每个子群，优化下面损失函数：
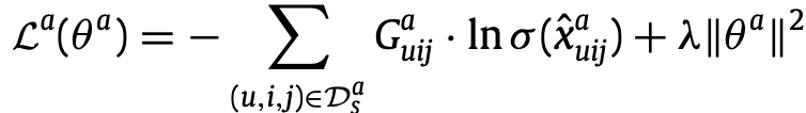
其中
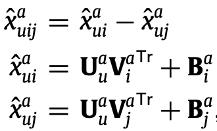
最终，物品u对i的预测得分为：
对每个用户，计算出它对该子群未观测过的物品的得分，选择得分最大的K个物品作为他在该子群的局部推荐列表
。
（3) 全局决策融合
LRGF框架中，用户的全局推荐列表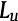
是由其的各个局部排序列表直接融合而成的，并不需要考虑用户对物品的局部预测评分。我们的列表融合算法有两个特点：
(a) order-scoring: 物品在局部排序列表的顺序反应了用户在该子群物品中的偏好顺序，这种局部的顺序关系在融合成全局列表时是必然要考虑的，这里定义用户u在子群a 中的局部列表中的物品v 的顺序得分为：
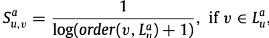
(b) group-aware：不同的子群有不同的成员组成，因此在融合的时候要考虑每个子群的特性。这里认为，如果一个用户在某个子群中给越多的物品打过分，则他在该子群的局部排序列表应该对全局列表贡献更多。这里定义物品v的在子推荐列表a中的子群得分为：
因此用户u 的在局部列表a 中每个物品的局部得分为：
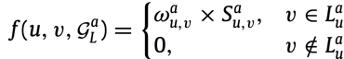
最终的用户u 的全局推荐列表是根据每个物品的全局得分来进行排序生成的，全局得分计算公式为：
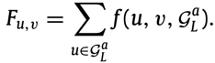
下图展示了LRGF框架的算法流程：
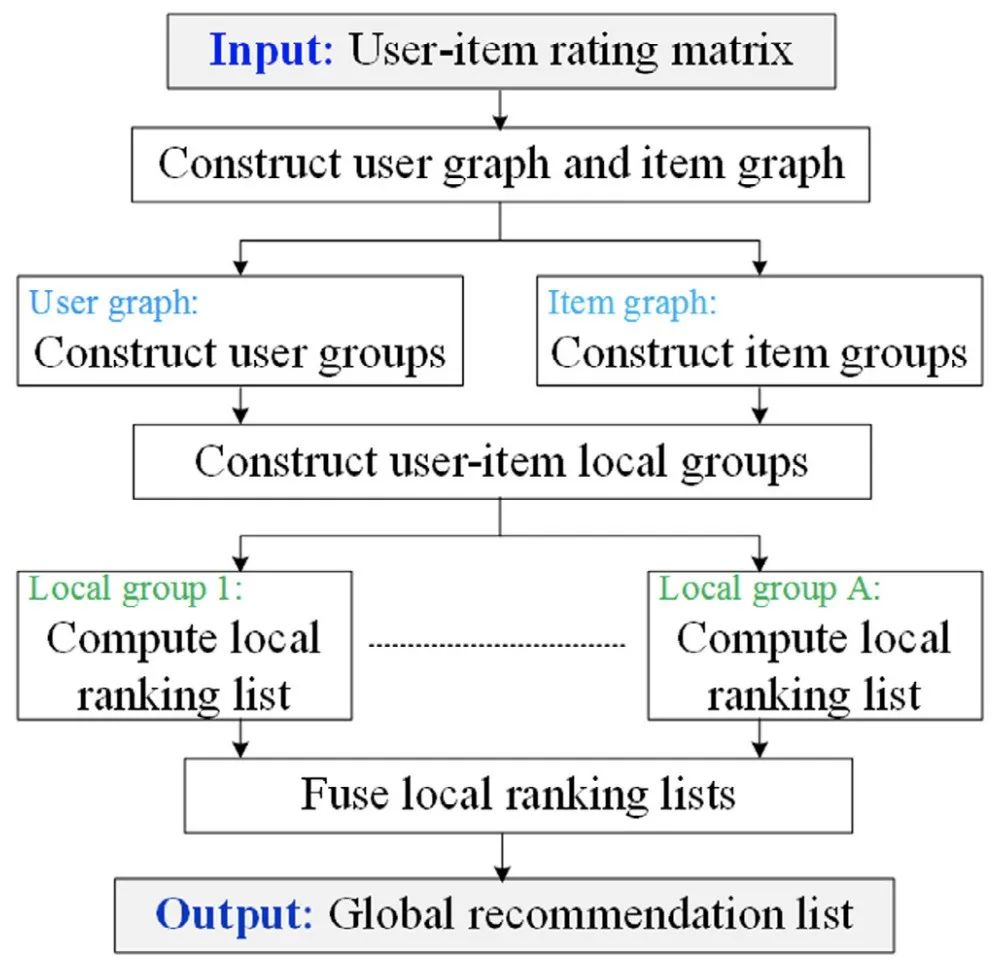
03
实验
1. 对比实验
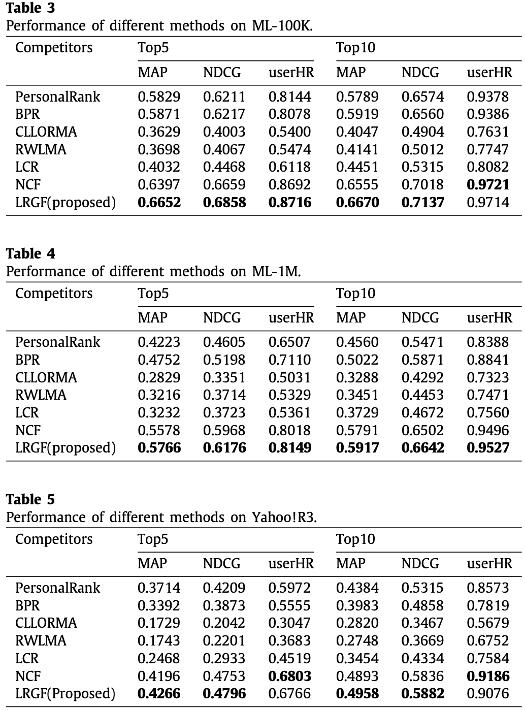
下面三个表分别表示在三个数据集上进行的对比实验，可以看出，
对比其他一些local-global模型，CLLORMA、RWLMA、LCR，LRGF框架能实现最好的结果，这证明了决策融合的有效性
LRGF的表现在绝大多数情况下要高于全局的排序模型，这证明了构建局部模型进行排序的优势
2. 消融实验
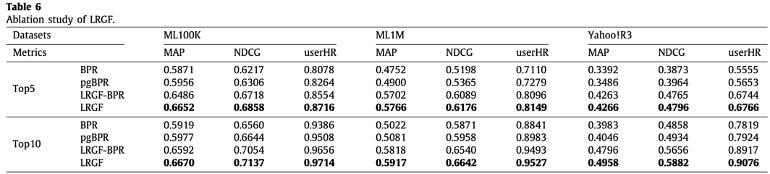
采用消融实验验证模型各个部分的有效性：
（1）对比BPR和pgBPR，或者LRGF-BPR和LRGF，可以看出pgBPR取得了一定的提升，无论是直接在全局建模还是局部建模
（2）对比BPR和LRGF-BPR，或者pgBPR和LRGF，可以看出无论排序模型使用BPR还是pgBPR，构建局部模型再融合的方式都要由于在全局直接排序的方式。
3. top-K实验
Top-k实验展现了推荐列表取不同长度时，不同算法的对比结果。
4. 局部列表长度变化
在进行全局列表融合时，局部列表的长度是其中一个超参数。通过该实验发现，局部列表的长度其实对全局融合的效果影响并不大。
04
结论
本文提出了一种局部排序-全局融合框架，允许使用多个更细粒度的特征空间进行排序学习。在局部排序时，采用两阶段随机游走构建子群，在每个子群中使用pgBPR算法进行排序学习；在全局融合阶段，采用了一种决策融合的方式直接将每个局部列表融合成全局的列表。实验结果证明了这种框架的有效性。
主要参考文献
[1] X. He, L. Liao, H. Zhang, L. Nie, X. Hu, T.-S. Chua, Neural collaborative filtering, in: Proceedings of the 26th International Conference on World Wide Web, WWW ’17, 2017, pp. 173–182, http://dx.doi.org/10.1145/3038912. 3052569.
[2] S. Rendle, C. Freudenthaler, Z. Gantner, L. Schmidt-Thieme, BPR: Bayesian personalized ranking from implicit feedback, in: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, UAI ’09, 2009, pp. 452–461.
[3] M. Zhang, B. Hu, C. Shi, B. Wang, Local low-rank matrix approximation with preference selection of anchor points, in: Proceedings of the 26th International Conference on World Wide Web Companion, No. 9, WWW ’17 Companion, 2017, pp. 1395–1403, http://dx.doi.org/10.1145/3041021. 3051148.
[4] X. Yang, B. Wang, Local matrix approximation based on graph random walk, in: Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR’19, 2019, pp. 1037–1040, http://dx.doi.org/10.1145/3331184.3331338.
[5] J. Lee, S. Bengio, S. Kim, G. Lebanon, Y. Singer, Local collaborative ranking, in: Proceedings of the 23rd International Conference on World Wide Web, No. 12, WWW ’14, 2014, pp. 85–96, http://dx.doi.org/10.1145/2566486. 2567970
以上是关于推荐系统｜局部排序-全局融合的top-n推荐的主要内容，如果未能解决你的问题，请参考以下文章