一文梳理推荐系统的中 EMBEDDING 的应用实践
Posted 浅梦的学习笔记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一文梳理推荐系统的中 EMBEDDING 的应用实践相关的知识,希望对你有一定的参考价值。
“ 自Embedding的概念问世以来,Embedding的探索和应用就没有停止过,Word2Vec、Sentence2Vec、Doc2Vec、Item2Vec,甚至Everything2Vec。对,“万物皆可Embedding”。几年来,Embedding在推荐系统中的应用也越来越多,方式众多,技法新颖。”
在之前的文章中,《文本内容分析算法》和《基于矩阵分解的推荐算法》文中都稍有提及Embedding的概念,由于Embedding太过重要,本文我们将详细讲解Embedding的相关知识,以及在推荐系统中的一些应用,因篇幅限制,关于Embedding在推荐系统中的应用实践我分为了两篇文章来讲述,本篇主讲Embedding以及相关延伸方法,另外一篇是大厂的Embedding实践应用,是更加偏tricks的一些应用实践总结。
Embedding的理解
Embedding,即嵌入,起先源自于NLP领域,称为「词嵌入(word embedding)」,主要是利用背景信息构建词汇的分布式表示,最终可以可以得到一种词的向量化表达,即用一个抽象的稠密向量来表征一个词。
从数学角度看,Embedding其实是一个映射(mapping),同时也是一个函数(function),即 ,该函数是injective(就是我们所说的单射函数,每个 只有唯一的 对应,反之亦然)和structure-preserving (结构保存,比如在X所属的空间上 ,那么映射后在 所属空间上同理 )的。那么对于Word Embedding,就是将单词映射到另外一个空间,这个映射也具有injective和structure-preserving的特点。
“嵌入”本身是一个数学概念。我们这里通俗理解,「如果将词看作是文本的最小单元,词嵌入本身是一种特别的映射过程,即将文本空间中的某个词,通过一定的方法,映射或者说嵌入到另一个数值向量空间,原来的整数全部变为实数,是用连续向量表示离散变量的方法。之所以称之为Embedding,是因为这种表示方法往往伴随着一种降维的意思,就像高维事物拍扁了嵌入到另一个低维空间中一样。」
Embedding这种向量化表达过程通常伴随以下变化:
-
高维——>低维 -
稀疏——>稠密 -
离散——>连续 -
整数——>实数
不难发现,「经过Embedding向量化表达后的数据,其实变得更加适合深度神经网络的训练和学习,也有利于工业界数据的工程化处理。」高维稀疏数据对于机器学习的参数学习和相关计算都不太友好(「高维易引发“维度之灾”,使空间距离很难有效衡量,另外高维经常使参数数量变得非常多,计算复杂度增加,也容易导致过拟合;稀疏容易造成梯度消失,导致无法有效完成参数学习」),因此通常特别稀疏的高维离散数据更适合使用Embedding代替传统One-Hot编码方式。
此外,「Embedding虽然是一种降维表示,但是却携带了语义信息,而且这种表示方式并不局限于词,可以是句子、文档、物品、人等等,Embedding能够很好地挖掘嵌入实体间的内部关联,即便降维也能保留这种潜在关系」,这简直就是“神来之笔”,怪不得说万物皆可Embedding。
词嵌入的维度表示某个隐含语义,一个词可能隐藏很多语义信息,比如北京,可能包含“首都、中国、北方、直辖市、大城市”等等,这些语义在所有文本上是有限的,比如 128 个,于是每个词就用一个 128 维的向量表达,向量中各个维度上的值大小代表了词包含各个语义的多少。
本质上来说,经过「Word Embedding」之后,各个单词就组合成了一个相对低维空间上的一组向量,这些向量之间的远近关系则由他们之间的语义关系决定。
因为上面提到的特性,使用Embedding可带来诸多好处:
-
不丢失信息的情况下降低维度 -
矩阵及向量运行便于并行 -
向量空间具有物理意义,比如可以根据距离比较相似性 -
可以在多个不同的维度上具有相似性 -
线性规则:king - man = queen - woman
Embedding的这种携带语义信息以及保留嵌入实体间的潜在关系的特性,使Embedding有了更多用武之地,例如:
-
「计算相似度」,比如 「man」和 「woman」的相似度比 「man」和 「apple」的相似度高 -
「在一组单词中找出与众不同的一个」,例如在如下词汇列表中: 「[dog, cat, chicken, boy]」,利用词向量可以识别出 「boy」和其他三个词不是一类。 -
「直接进行词的运算」,例如经典的: 「woman + king-man = queen」 -
「表征文本」,如累加得到一个文本的稠密向量,或平均表征一个更大的主体; -
「方便聚类」,会得到比使用词向量聚类更好的语义聚类效果。 -
「由于携带了语义信息,还可以计算一段文字出现的可能性」,也就是说,这段文字是否 「通顺」。
上面的嵌入实体是单词,如果换成推荐物品(item),上面的一些用法,是不是让你眼前一亮呢?
Word2Vec
:books: Distributed Representations of Words and Phrases and their Compositionality
:books: word2vec Parameter Learning Explained
:books: word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method
词嵌入表示通常会用到谷歌提出的 Word2Vec工具库,另外fastText和TensorFlow中也可以实现Embedding的功能。这个小节我们借助Word2Vec工具的模型实现来更加深入理解Embedding。
Word2Vec的原理
Word2Vec 是用浅层神经网络学习得到每个词的向量表达,而且在工程上进行了优化,使得百万词的规模在单机上可以几分钟轻松跑出来。它有两种网络结构,分别是CBOW(Continues Bag of Words)和Skip-gram,两种网络结构图见下图。
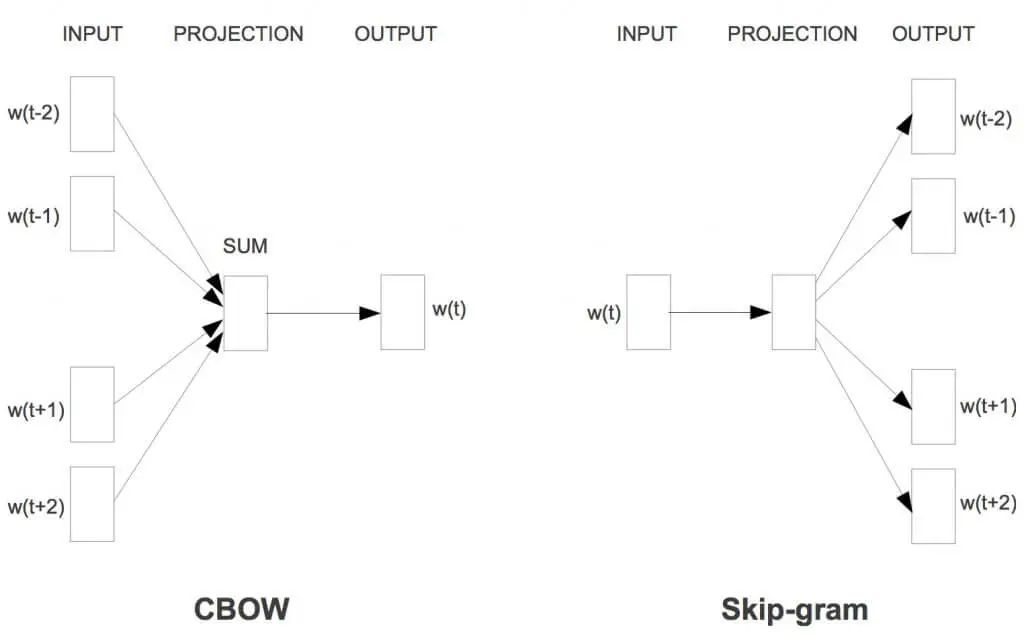
这两种结构都是假定每个词都跟其相邻的词的关系最密切,不同的是CBOW模型的动机是每个词都是由相邻的词决定的,所以CBOW的输入是 周边的词,预测的输出是 ,而Skip-gram模型的动机则是每个词都决定了相邻的词,输入是 ,输出是 周边的词。这里相邻的词通常由一个滑动窗口来获得,滑动窗口的长度为2c+1(目标词前后各选c个词),从句子左边滑倒右边,每滑一次,窗口中的词就形成了我们的一个正样本。如上图,这里的c设为2,其中 是当前所关注的词, 、 、 、 是上下文中出现的词。
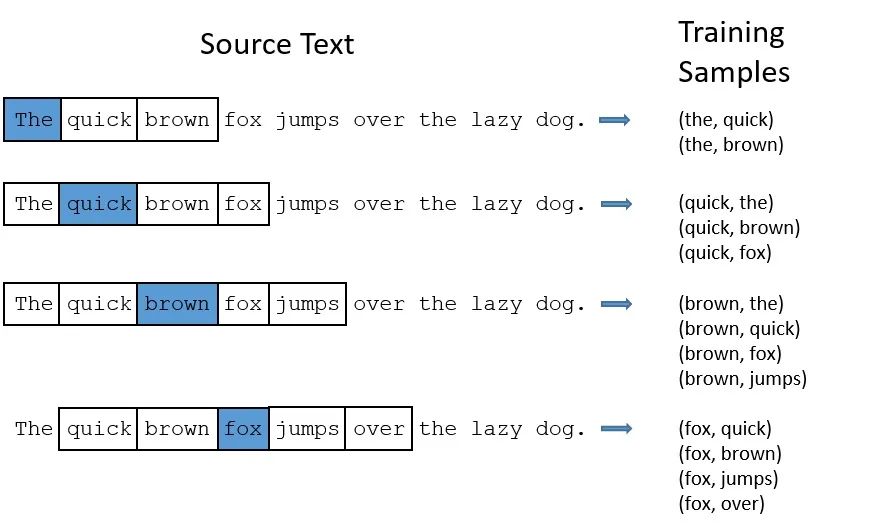
经验上讲Skip-gram的效果要更好一点,我们以Skip-gram为例,理解一下原理。上面讲到通过滑动窗口可以获取到训练样本,有了训练样本之后我们就可以着手定义优化目标了,既然每个词 都决定了相邻词 ,基于极大似然,我们希望所有样本的条件概率 之积最大,于是有:
转为最大化对数似然:
其中,T是文本长度,即单词总数,c是窗口大小,另外单词一般需要先用One-Hot编码。
其实从上面的图中可以看出,在实际训练学习过程中,训练样本是由中心词和其上下文词组成一个个Pair对,那我们可以将目标函数写成一个更容易理解的的式子:
其中, 表示中心词 与其上下文词 构成的样本对, 是语料中所有单词及其上下文词构成的样本对集合,这里的 为「待定参数集」。
接下来的问题是怎么定义 ,作为一个多分类问题,最简单最直接的方法当然是直接用Softmax函数,同时我们希望用隐向量来表示每个词。
于是设 为中心词w的词向量, 为上下文词c向量,向量维度等于设置的隐藏层单元数量。整个语料共有V个单词,也就是词汇表单词数。
因此:
带入上面的目标函数,可以得到:
其中,参数 是 和 , , 是向量维度。
这两个单词的隐向量的点积表示语义的接近程度,其实点积的物理意义就是词之间的距离,点积越大,表明两个单词的语义越接近,向量点积展开如下:
(注:向量点积在不同的论文有不同的表示形式,本文为了推导后面的负例采样优化,写法与第三篇论文的写法保持一致。)
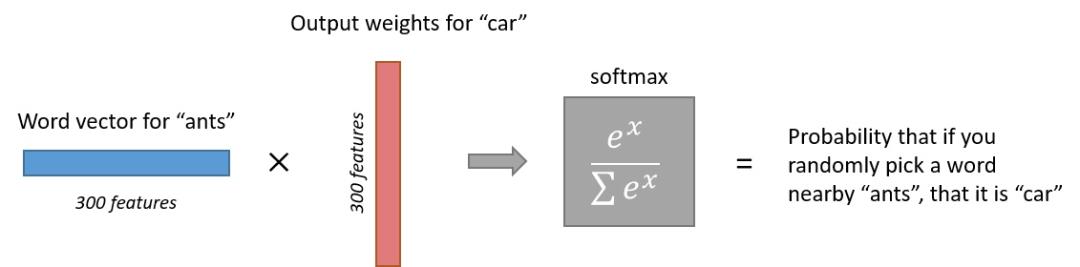
而Softmax的作用就是将点积转换成概率,下图的例子可以辅助理解[^1]:
Word2Vec的网络结构
CBOW和Skip-gram都可以表示成由输入层(Input)、映射层(Projection)和输出层(Output)组成的神经网络。
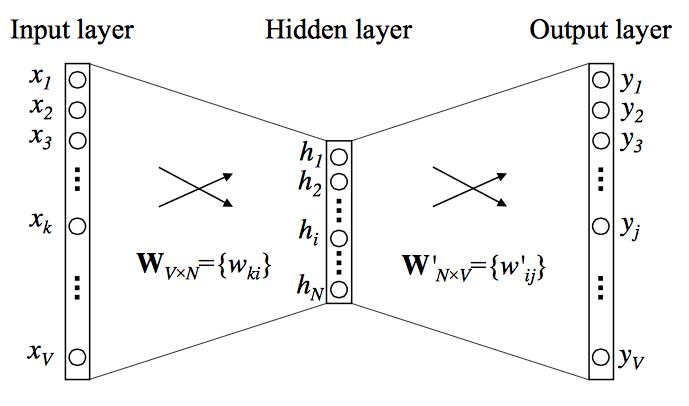
输入层中的每个词通常由独热编码(One-Hot)方式表示,即所有词均表示成一个 维向量,其中 为词汇表中单词的总数。在向量中,每个词都将与之对应的维度置为1,其余维度的值均设为0。
在映射层(也就是隐含层)中, 个隐含单元(Hidden Units)的取值可以由 维输入向量以及连接输入和隐含单元之间的 维权重矩阵 计算得到。在CBOW中,还需要将各个输入词所计算出的隐含单元求和。需注意的是,「Word2Vec网络中的隐含层没有使用任何非线性激活函数,或者可以勉强说用的是线性激活函数(Linear Activation Function)。因为Word2Vec不是为了做语言模型,它不需要预测的更准,加入非线性激活函数没有什么实际意义,反而会降低Word2Vec的性能。」
同理,输出层向量的值可以通过隐含层向量,以及连接隐含层和输出层之间的 维权重矩阵 计算得到。输出层也是一个 维向量,每维与词汇表中的一个单词相对应。最后,对输出层向量应用Softmax激活函数,可以计算出每个单词的生成概率。
再之后,利用反向传播来训练神经网络的权重即可。
不过上图的网络结构是单个上下文的一个示例,即当前词预测下一个词,对于真正的多词上下文的CBOW和Skip-gram,通常是下面的结构:
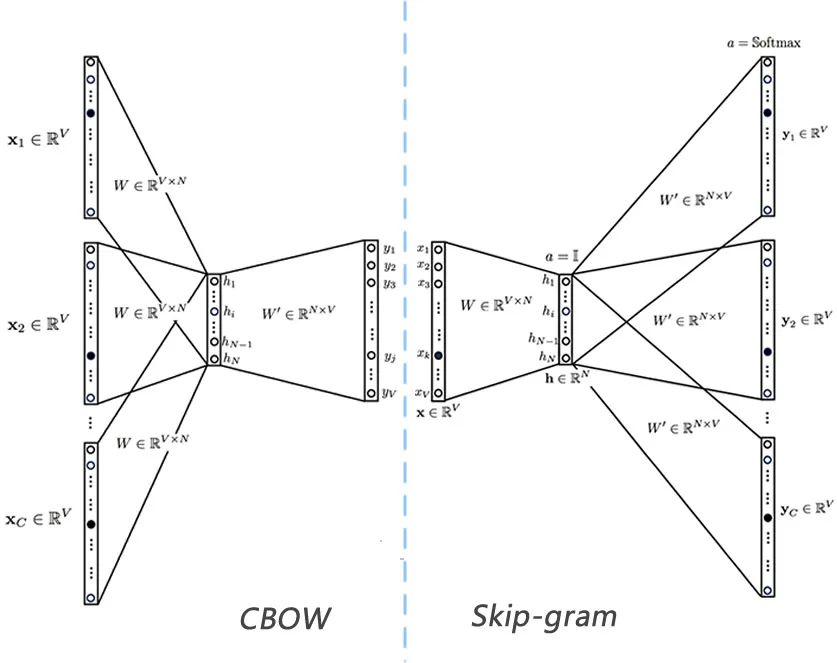
以Skip-gram模型为例,其前向公式为:
因为输出层共享权重 ,所以 都是一样的,输出向量 也是都一样的,即 。
如果想更详细地了解CBOW和Skip-gram的原理、后向传播、示例讲解等,推荐查看
以上是关于一文梳理推荐系统的中 EMBEDDING 的应用实践的主要内容,如果未能解决你的问题,请参考以下文章