布隆过滤器

Posted 2021-05-01 mikeDi智能世界

布隆过滤器的原理

布隆过滤器是一种多哈希函数映射的快速查找算法。它可以判断出某个元素肯定不在集合里或者可能在集合里，即它不会漏报，但可能会误报。通常应用在一些需要快速判断某个元素是否属于集合，但不严格要求100％正确的场合。

基本原理

1. 一个空的布隆过滤器是一个m位的位数组， m是由存入的元素n决定的， 一般m=n*c (c为某一个固定的常数)，初始时m所有位的值都为0。 

2. 定义了k个不同的符合均匀随机分布的哈希函数，每个函数把集合元素映射到位数组的m位中的某一位。
   

添加一个元素：

先把这个元素作为k个哈希函数的输入，拿到k个数组位置，然后把所有的这些位置置为1。

查询一个元素（测试这个元素是否在集合里）：

把这个元素作为k个哈希函数的输入，得到k个数组位置。这些位置中只要有任意一个是0，元素肯定不在这个集合里。如果元素在集合里，那么这些位置在插入这个元素时都被置为1了。如果这些位置都是1，那么要么元素在集合里，要么所有这些位置是在其他元素插入过程中被偶然置为1了，导致了一次“误报”。

一个布隆过滤器的例子见下图，代表了集合{x,y,z}。带颜色的箭头表示了集合中每个元素映射到位数组中的位置。元素w不在集合里，因为它哈希后的比特位置中有一个值为0的位置。在这个图里，m=18,k=3。

一个布隆过滤器的例子

简单的布隆过滤器不支持删除一个元素，因为“漏报”是不允许的。一个元素映射到k位，尽管设置这k位中任意一位为0就能够删除这个元素，但也会导致删除其他可能映射到这个位置的元素。因为没办法决定是否有其他元素也映射到了需要删除的这一位上。

通过好几个哈希函数来共同判断这个元素是否在集合里，比只用一次哈希带来冲突的可能性要低很多。暴雪的MPQ归档文件中使用的哈希算法跟布隆过滤器也有异曲同工之妙。

误判率

当误判率<=1%时, m/n是9.6，即m=n*9.6，此时k=6.72，即7bit，即需要7次hash，每个元素占7bit作为布隆过滤器的位数组数据。

上面也就是说，我们存1亿个数据，此时要建立9亿个位的bit作为布隆向量。然后再找7个hash函数。将1亿数中的每个数经过7个hash函数得到7个数，分别将布隆向量7个位置置为1.

查的过程，同样作相同过程操作，看这7位是否为1.如果都是，则表示存在该元素。

误差率，m和n、k的关系如下面部分分析。

误判率就是在插入n个元素后，某元素被判断为“可能在集合里”，但实际不在集合里的概率，此时这个元素哈希之后的k个比特位置都被置为1。

假设哈希函数等概率地选择每个数组位置，即哈希后的值符合均匀分布，那么每个元素等概率地哈希到位数组的m个比特位上，与其他元素被哈希到哪些位置无关(独立事件)。设定数组总共有m个比特位，有k个哈希函数。在插入一个元素时，一个特定比特没有被某个哈希函数置为1的概率是：

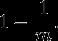
插入一个元素后，这个比特没有被任意哈希函数置为1的概率是：

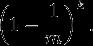
在插入了n个元素后，这个特定比特仍然为0的概率是：

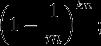
所以这个比特被置为1的概率是：

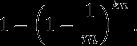
现在检测一个不在集合里的元素。经过哈希之后的这k个数组位置任意一个位置都是1的概率如上。这k个位置都为1的概率是：

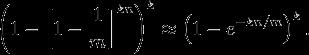
哈希函数个数的最优解

对于给定的m和n，让“误报率”最小的k值为：

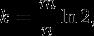
此时“误报率”为：

可以简化为：

在leveldb中，

设定的误判率<=1%,所以m/n是9.6，即10个比特，此时k=6.72，即7bit，即需要7次hash，每个元素占7bit，总共需要m=n*9.6个比特作为布隆过滤器的位数组数据。

优点

1. 存储空间和插入/查询时间都是常数，远远超过一般的算法

2. Hash函数相互之间没有关系，方便由硬件并行实现

3. 不需要存储元素本身，在某些对保密要求非常严格的场合有优势

缺点

1. 有一定的误识别率

2. 删除困难

应用

1. 搜索引擎中的海量网页去重

2. leveldb等数据库中快速判断元素是否存在，可以显著减少磁盘访问