布隆过滤器来了解一下?
Posted 搬砖攻城师
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了布隆过滤器来了解一下?相关的知识,希望对你有一定的参考价值。
布隆过滤器应用于最近比较火的海量处理问题。可以快速判断一个元素在不在海量数据的集合当中。缺点是有一定的失误率,优势是占用内存较少。
这一天,程序媛小王去一家互联网公司面试。
面试官问了这样一个问题:不安全网页的黑名单里有100亿个URL,每一个网页的URL最多占用64B。要求实现一种过滤系统,可以根据网页的URL判断是否在这个黑名单中。
小王: 可以将所有url保存在一个集合里,然后通过比较判断黑名单里有没有。
面试官:你那具体要怎么实现呢?请告诉我你存储需要的存储空间具体是多少?
小王:使用HashSet,内存大概需要100亿*64B=640GB。
面试官(面无表情):“这个空间太大了,要求的额外的空间不能超过30GB,有没有一种更好的算法?
小王:emmm
面试官:提示你一下,这个系统允许有万分之一的失误率。
这时候我们的布隆过滤器可以就派上用场。
布隆过滤器本质上是一个bit数组,可以用极少的空间解决“判断在不在”这种问题。
以这道题为例,小王是思路是将所有的URL整个都存储起来,但是这个题目其实只需要我们判断在不在,我们根本无需存整个URL,甚至无需在意一个URL是多少字节,只需要存这个URL是“在”还是“不在”这两种状态就好了。
讲到这里不知读者有没联想我们计算机世界的0和1。我们完全可以用一个容器存放这两种状态,在黑名单URL用1来表示,不在黑名单用0来表示。
接下来我们就使用布隆过滤器着手解决这道题。
首先创建一个bit数组,数组里所有位置初始化都为0。然后100亿个URL每一个都做hash运算,每一次得出的结果在bit数组对应的下标位置把0变成1。有URL对应的数组位置会被我们“标记”。当100亿个URL改变了bit数组里对应位置的值后,就得到我们所需要的布隆过滤器
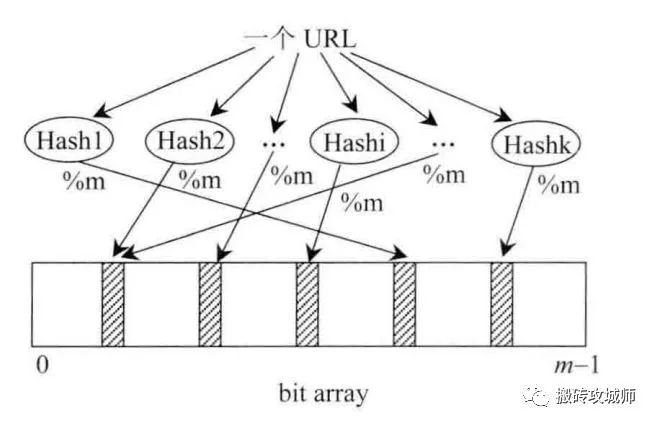
重头戏来了,当我们需要判断一个URL在不在黑名单里,只需要判断URL在经过hash函数后对应的bit数组下标的位置是“0”还是“1”。如果对应位置是0,意味这个位置仍是初始化状态,没有被标记过,所以这个URL不在黑名单里。如果对应位置是1,意味这个位置已经被标记过,所以这个URL在黑名单里。
讲到这里,读者可能已经有一个“布隆过滤器器就是一个bit数组的”模糊全局概念。因为以上描述只是为了让读者知道布隆过滤器是个啥。
接下来,请看几个布隆过滤的重要知识点。
上面所提到的“100亿个URL每一个都做hash运算”,这里的hash运算在现实中不只是一个hash函数,而是一组hash函数。
顺便说一句hash函数不需要自己实现,经典的哈希函数已经有很多了,比如MD5、SHAI。
但为什么URL经过hash函数的出来的值一定会是bit数组下标?
打个比方,一个最简单的hash运算:%3。集合里的数经过%3的hash运算后,是只可能得出0或1或2,这三种情况。也就是说hash运算得出的输出域是固定的。
这是hash函数的一个重要性质:哈希函数有无限的输入域,但只有固定有限输出域。
布隆过滤器是有一定失误率。它的误判类型是——宁可错杀一百,也不能放过一个。也就是说如果URL在黑名单,判断结果一定会表示在。可能失误的情况是:某个URL不在黑名单里,也被判断在。
为什么布隆过滤器会失误?并且只会“冤枉”,不会“漏判”?
这是因为hash函数的另一个性质:不同的输入值hash运算后得到的散列输出值可能不同,也可能相同。但是不同的散列输出值对应的输入值一定不同。
假如要判断的两个URLhash运算得到了相同的结果,但一个在黑名单里,一个不在黑名单里,对应的数组下标位置已经被描黑,那么两个URL都会被判为在黑名单里。
想要减少失误率就需根据三个公式设计一个长度合适的bit数组。
还是上面那道题为例,n是样本量,即100亿;p预期失误率,即0.0001,m是数组元素个数。
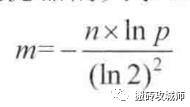
01
公式一:计算布隆过滤器的大小
把p和n代入公式match,lnp等于-9.21,(ln2)的平方是0.7,n是100亿
计算出来m等于19.19n,转为GB,等于bit数组大小要开25G
02
公式二:我们还得确定hash函数的个数,哈希函数的个数k公式:
算出k为14,需要14个hash函数
03
公式三:计算失误率,p公式:
算出失误率是0.006%。
此时小王可以自信的回答面试官“可以使用布隆过滤器,布隆过滤器是xxx。如果布隆过滤器的大小开25g,那么有0.006%的失误率,内存和失误率都满足要求。”
布隆过滤器可以解决许多问题,比如:网页URL的去重,缓存穿透,垃圾邮件的判别等问题。
这里重点介绍一下布隆过滤器如何解决缓存穿透的问题。
缓存穿透,简单来说就是因为有海量的不存在的key请求,导致缓存起不了作用,大量请求引向数据库,导致数据库宕机。
但当有人恶意攻击,把发起海量的不存在的key请求,由于都是不存在的请求,缓存自然查不到,这些海量的请求就会都会落到数据库中。导致数据库崩溃。
一般解决方案是:缓存空数据,如果某key数据库查询结果为空,则把这个不存在值的key也缓存起来,设置较短过期时间,当后续又出现该key时,就可以在缓存里查询到了,不再请求数据库。但是如果有人恶意攻击,key是随机生存的,请求的key是大量而不重复,这样的做法就用处不大了。
用布隆过滤器解决:是请求过来,先调用布隆过滤器判断数据是否存在。如果不存在的数据,就不要把请求引向数据库。直接过滤掉了大量不存在的数据攻击。
总的来说,当数据量比较大并且重复率不高的时候,布隆过滤器的成本比一般解决方案成本更低。
看了这篇文章,不如乘热打铁,做道题目看看感觉如何
以上是关于布隆过滤器来了解一下?的主要内容,如果未能解决你的问题,请参考以下文章