堆排序就这么简单

Posted 2021-05-01 Java3y

一、堆排序介绍

来源百度百科：

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。

前面我已经有二叉树入门的文章了，当时讲解的是二叉查找树，那上面所说的完全二叉树是怎么样的一种二叉树呢？？还有满二叉树又是怎么的一种二叉树呢？？甚至还有完满二叉树？？

• 完全二叉树： 除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐。

• 满二叉树：除了叶子结点之外的每一个结点都有两个孩子，每一层(当然包含最后一层)都被完全填充。

• 完满二叉树：除了叶子结点之外的每一个结点都有两个孩子结点。

下面用图来说话：

• 完全二叉树(Complete Binary Tree)：

• 满二叉树(Perfect Binary Tree)：

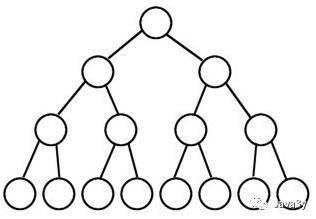
• 完满二叉树(Full Binary Tree)：

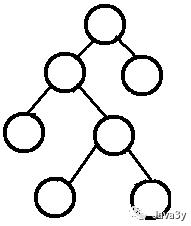
参考资料：

• http://www.cnblogs.com/idorax/p/6441043.html

简单来说：堆排序是将数据看成是完全二叉树、根据完全二叉树的特性来进行排序的一种算法

• 最大堆要求节点的元素都要不小于其孩子，最小堆要求节点元素都不大于其左右孩子

• 那么处于最大堆的根节点的元素一定是这个堆中的最大值

这里我们讨论最大堆：当前每个父节点都大于子节点

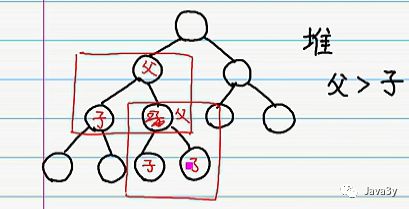
完全二叉树有个特性：左边子节点位置 = 当前父节点的两倍 + 1，右边子节点位置 = 当前父节点的两倍 + 2

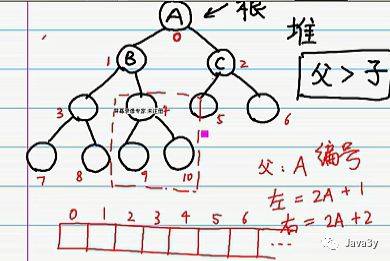
二、堆排序体验

现在我们有一个完全二叉树：左子树和右子树都符合最大堆-->父>子

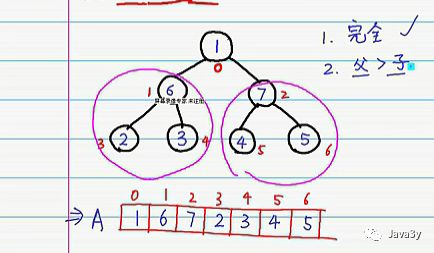
但是我们会发现：根元素所在的数并不符合，明显的是：1是小于7的

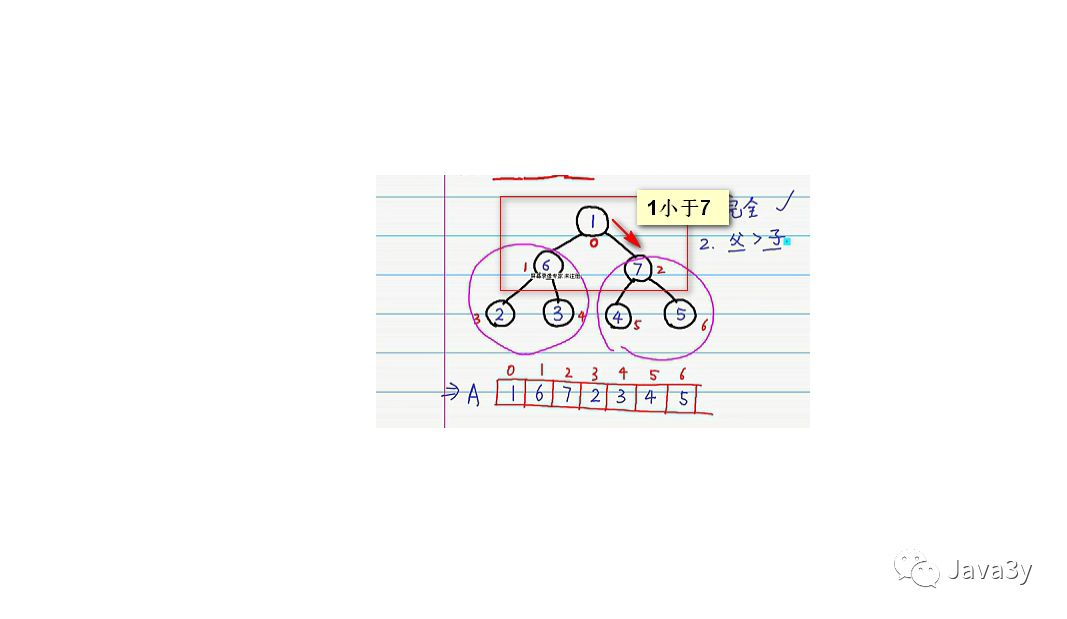
我们就对其进行交换，交换完之后我们会发现：右子树又不符合了～

因为，右子树变成了这样：

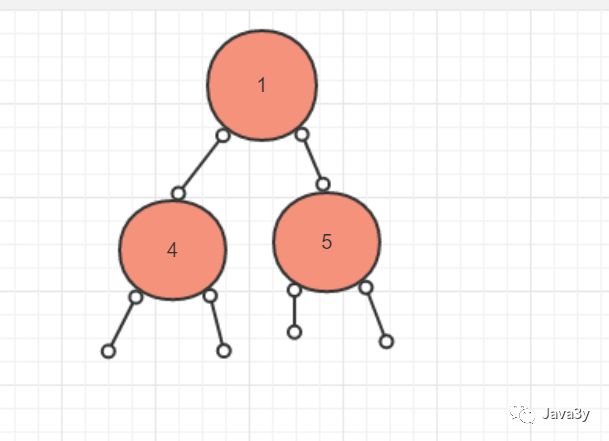
最后，我们将右子数的最大值也交换到右子树的根元素上

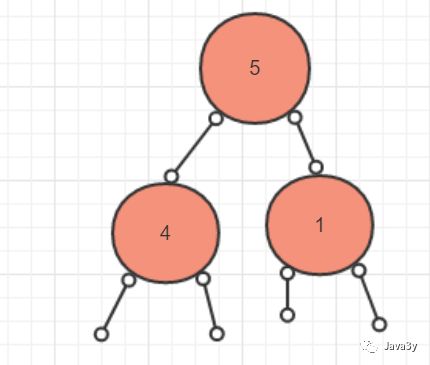
于是我们第一次的建堆操作就完成了！

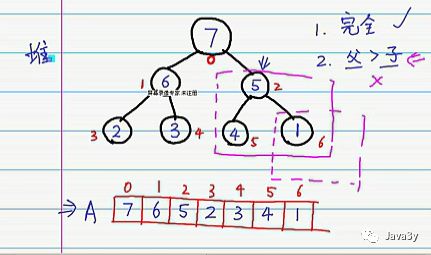
可以发现的是：一次堆建立完之后，我们的最大值就在了堆的根节点上

随后将堆顶最大值和数组最后的元素进行替换，我们就完成了一趟排序了。

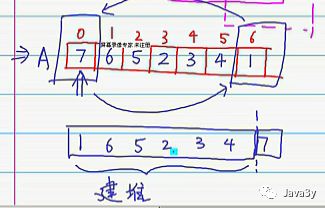
接下来，剩下的数不断进行建堆，交换就可以完成我们的堆排序了

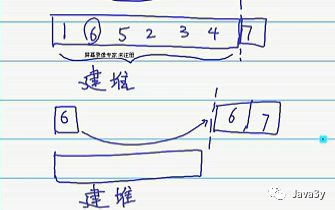
………建堆，交换….建堆，交换…建堆，交换…建堆，交换..

三、堆排序代码实现

比较当前父节点是否大于子节点，如果大于就交换，直到一趟建堆完成～

    /**
     * 建堆
     *
     * @param arrays          看作是完全二叉树
     * @param currentRootNode 当前父节点位置
     * @param size            节点总数
     */
    public static void heapify(int[] arrays, int currentRootNode, int size) {

        if (currentRootNode < size) {
            //左子树和右字数的位置
            int left = 2 * currentRootNode + 1;
            int right = 2 * currentRootNode + 2;

            //把当前父节点位置看成是最大的
            int max = currentRootNode;

            if (left < size) {
                //如果比当前根元素要大，记录它的位置
                if (arrays[max] < arrays[left]) {
                    max = left;
                }
            }
            if (right < size) {
                //如果比当前根元素要大，记录它的位置
                if (arrays[max] < arrays[right]) {
                    max = right;
                }
            }
            //如果最大的不是根元素位置，那么就交换
            if (max != currentRootNode) {
                int temp = arrays[max];
                arrays[max] = arrays[currentRootNode];
                arrays[currentRootNode] = temp;

                //继续比较，直到完成一次建堆
                heapify(arrays, max, arrays.length);
            }
        }
    }

值得注意的是：在上面体验堆排序时，我们是左子树和右子数都是已经有父>子这么一个条件的了。

• 显然，一个普通的数组并不能有这种条件(父>子)，因此，我们往往是从数组最后一个元素来进行建堆

    /**
     * 完成一次建堆，最大值在堆的顶部(根节点)
     */
    public static void maxHeapify(int[] arrays, int size) {

        // 从数组的尾部开始，直到第一个元素(角标为0)
        for (int i = size - 1; i >= 0; i--) {
            heapify(arrays, i, size);
        }

    }

完成第一次建堆之后，我们会发现最大值会在数组的首位：

接下来不断建堆，然后让数组最后一位与当前堆顶(数组第一位)进行交换即可排序：

    for (int i = 0; i < arrays.length; i++) {

        //每次建堆就可以排除一个元素了
        maxHeapify(arrays, arrays.length - i);

        //交换
        int temp = arrays[0];
        arrays[0] = arrays[(arrays.length - 1) - i];
        arrays[(arrays.length - 1) - i] = temp;

    }

四、总结

堆排序是比其他排序要难一点，他用到了完全二叉树这么一个特性来进行排序，代码实现上也比其他排序要复杂一点。

参考资料：

• http://www.cnblogs.com/skywang12345/p/3602162.html