一文读懂堆排序
Posted 算法爱好者
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一文读懂堆排序相关的知识,希望对你有一定的参考价值。
(点击上方公众号,可快速关注)
https://61mon.com/index.php/archives/202/
堆排序是利用堆的性质进行的一种选择排序。下面先讨论一下堆。
堆实际上是一棵完全二叉树,其满足性质:任何一结点大于等于或者小于等于其左右子树结点。
堆分为大顶堆和小顶堆,满足 “任何一结点大于等于其左右子树结点” 的称为大顶堆,满足 “任何一结点小于等于其左右子树结点” 的称为小顶堆。
由上述性质可知:大顶堆的堆顶肯定是最大的,小顶堆的堆顶是最小的。
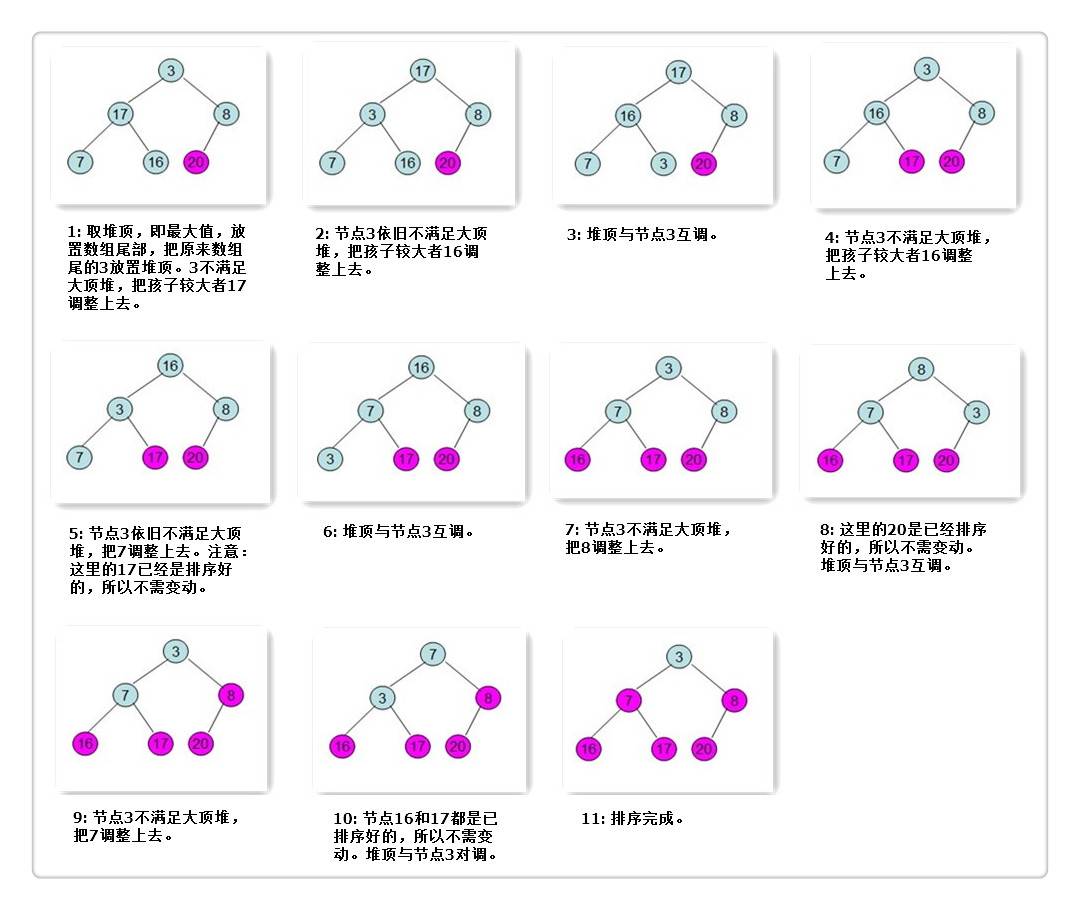
下面举个例子(资源来自堆排序 - 海子)来说明堆排序的过程(以升序为例):
给定整型数组:{16, 7, 3, 20, 17, 8},根据该数组 “构建” 完全二叉树(并不是真的写代码去构建,只是把数组看成完全二叉树去操作)。
程序从最后一个非叶子结点开始,即 3。判断其左右孩子:8,8 比 3 大,把 8 调整上去。
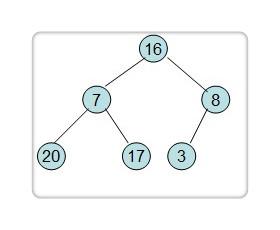
3 结点下无孩子,判断结束。
继续往前一步,至 7 结点,判断其左右孩子:20 和 17,20 是最大的,将其调整上去。
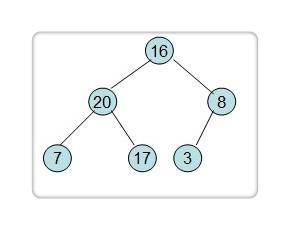
7 结点下无孩子,判断结束。
继续往前一步,至 16 结点,判断其左右孩子:20 和 8,20 是最大的,将其调整上去。
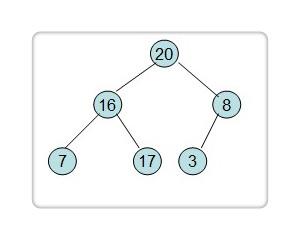
判断 16 结点下左右孩子:7 和 17,17 是最大的,将其调整上去。
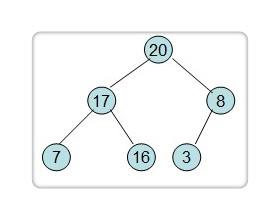
16 结点下无孩子,判断结束。
遍历已至头部,结束。
至此数组已经满足大顶堆的性质,接下来的操作就很简单了。
看完上面所述的流程你至少有两个疑问:
1、如何确定最后一个非叶子结点?
其实这是有一个公式的,设二叉树结点总数为 n,则最后一个非叶子结点是第 ⌊n2⌋ 个。
2、数组当中如何确定当前结点的左右孩子位置?
设当前结点下标是 i,则其左孩子的下标是 2i,右孩子的下标是 2i+1。请注意:这是建立在数组下标从 1 开始的情况。若数组下标从 0 开始,则其左右孩子下标还各需多加一个 1。
以下代码默认数组下标从 1 开始,请读者注意。
/* 已知 array[left]...array[right] 的值除 array[left] 之外均满足堆的定义,
本函数调整 array[left],使 array[left]...array[right] 成一个大顶堆 */
void HeapAdjust(int array[], int left, int right)
{
int index = left;
for (int i = left * 2; i <= right; i = i * 2)
{
if (i < right && array[i] < array[i + 1]) // 找到孩子中较大者
i++;
if (array[index] > array[i])
return;
swap(array[index], array[i]);
index = i;
}
}
void HeapSort(int array[], int left, int right)
{
int len = right - left + 1;
for (int i = len / 2; i >= left; i--) // 把数组调整成大顶堆
HeapAdjust(array, i, right);
for (int i = right; i > left; i--) // 排序
{
swap(array[left], array[i]);
HeapAdjust(array, left, i - 1);
}
}
时间复杂度为 O(nlogn),证明如下。
首先计算建堆的时间,也就是下面的代码,
for (int i = len / 2; i >= left; i--) // 把数组调整成大顶堆
HeapAdjust(array, i, right);
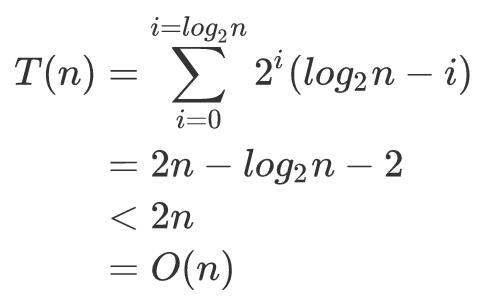
接下来就是排序的时间,即下面的代码:
for (int i = right; i > left; i--) // 排序
{
swap(array[left], array[i]);
HeapAdjust(array, left, i - 1);
}
HeapAdjust( ) 耗时 logn,共 n 次,故排序时间为 O(nlogn)。
综上所述,堆排序时间复杂度为 T(n)=O(n)+O(nlogn)=O(nlogn)。
觉得本文有帮助?请分享给更多人
关注「算法爱好者」,修炼编程内功
淘口令:复制以下红色内容,再打开手淘即可购买
范品社,使用¥极客T恤¥抢先预览(长按复制整段文案,打开手机淘宝即可进入活动内容)
以上是关于一文读懂堆排序的主要内容,如果未能解决你的问题,请参考以下文章