图解排序算法：堆排序

Posted 2021-05-01 纯文笔记

堆与树

很多朋友看到堆排序时，很可能是从冒泡等各种排序算法一路看过来的，其对于堆这种数据结构并无概念。

因此我们先对堆及相关数据结构的概念做个基本介绍。

二叉堆是一种完全二叉树。

树又是怎样的数据结构？

之前，我们接触的常用数据结构如链表、栈、队列等，都是线性结构的，也就是一个节点的左右最多只有一个节点，故而在某些场景中，它们的使用效率太低。而树则不同，它的每个节点可以有N个节点。

（注意：没有任何一种数据结构能通用所有场景，在不同场景中各种数据结构有不同的优劣势）

什么是树

树是包含n个节点的有空合集，n>0。先看一张树的例图。

根据上图，我们来理一理树的一些概念：

1. 每个节点有0至多个子节点；
2. 每个子节点只有一个父节点；
3. 没有父节点的节点称之为根节点，或者树根；
4. 没有子节点（或说子节点为0个）的节点称之为叶节点；
5. 节点的度：即节点的宽度（分支数量），指节点含有几个子节点，如节点12的度为2，节点15的度为3；
6. 树的度：即树的最大宽度，以最大度节点的度为准，如上图中节点20的度最大，所以整个树的度为4；
7. 树的高度： 即从树根开始到叶节点的最长路径（层次），如上图中树的高度为4（路径15-20-13-36或15-20-13-19）；
8. 子树：由每个节点及其下面的子节点、孙节点、叶节点等所有节点组成。如子树20的高度为3，子树13的高度为2。
9. 多叉树：每个节点最多有N个子节点（宽度、分支为N），称之为N叉树。如上图可称为4叉树。同理，二叉树即为所有节点最多只有2个子节点的树（子节点范围为0、1、2个）。

根据树的不同特征，有一些比较特殊的树，下面做个简单的介绍。

满二叉树

1：除了最后一层，其余层次的所有节点都有2个子节点。

2：其叶节点全部在最后一层，上面层次不存在叶节点。

完全二叉树

1：除了最后一层与其上一层，其余层次的所有节点都有2个子节点

2：最后一层的叶节点从左向右紧密相连排列，中间不能有空缺。

开篇即说二叉堆是一种完全二叉树，所以请注意它的特性，下文会用到。

上图中，右侧那个不是完全二叉树，因为最后一层的叶节点不是从左向右紧密相连，中间有空缺。

可以发现，满二叉树满足完全二叉树的特征，因此它也算一种特殊的完全二叉树。

二叉搜索树/BST树

仅作了解，与堆排序无关。

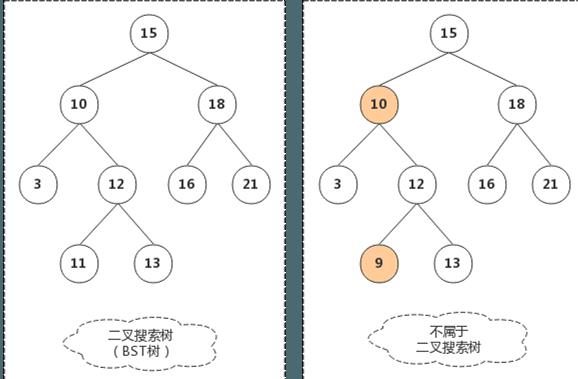
对任意一个父节点，其左支所有节点都比它的值小，其右支所有节点都比它的值大，这样特征的二叉树被称为二叉搜索树（BST树）。

上图左侧为一个二叉搜索树，而右侧不是，因为10的右支中出现了比它小的节点，而按照定义，任意一个节点，其右支的所有节点都必须比它大。

要在二叉搜索树中检索某个值，先从根节点开始比对，如该值小，说明该值不可能出现在右支，因此往左支继续比对；如该值大，则往右支节点比对下去……如此循环比对下去。

平衡二叉树/AVL树

仅作了解，与堆排序无关。

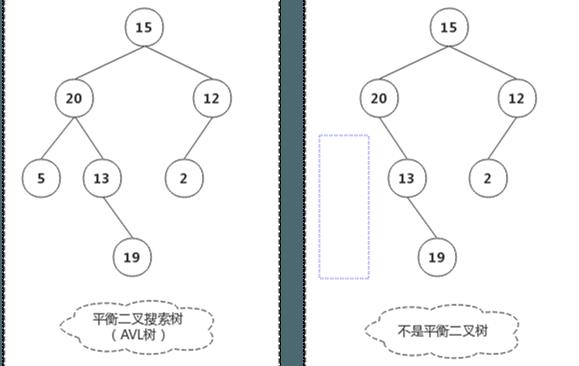
对于整个树及任意一个子树，其左支高度与右支高度相差不超过1，则称之为平衡二叉树（AVL树）。

上图中，左侧为AVL树，而右侧不是。因为虽然对于子树20来说，其左支高度为1，右支高度为3（从子树根节点20算起），高度相差为2，不符合AVL树的定义。

二叉堆

上文对树做了简单的概念介绍，对我们理解堆排序有很好的铺垫作用。

二叉堆是一种完全二叉树，但完全二叉树只是拥有结构特征，对各节点的值没有要求。而二叉堆则不同，它除了据有完全二叉树的结构特征，其节点的值另有特性。

二叉堆分为最大堆与最小堆，也有叫法是大顶堆/大根堆、小顶堆/小根堆。

对于最大堆来说，任意一个父节点的值都大于或等于它的子节点；

对于最小堆来说，任意一个父节点的值都小于或等于它的子节点。

从上面的特征可以发现，最大堆的根是整个堆中的最大值；最小堆的根是整个堆中的最小值。

综合来说，二叉堆有2个特性，将在堆排序中用到：其一，完全二叉树的结构特性；其二，最小堆/最大堆的父子节点值大小特性。

请记住二叉堆的特性，堆排序就是根据此特性演算的。

用图来说明。

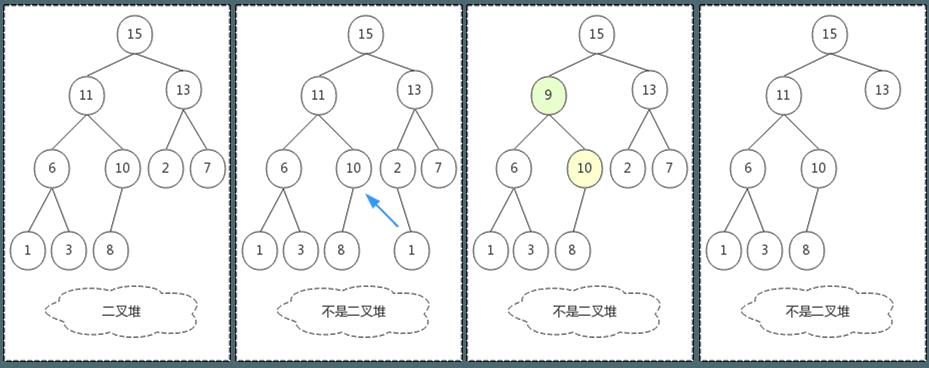
左一为二叉堆；左二不是，因为它最后一层叶子节点之间有空缺，不符合完全二叉树的特征；左三也不是，因为它不符合堆的父子节点值大小特性；左四也不是，因为它不符合“除最后一层和上一层外，其余节点都必须有2个子节点”的特性。

堆/子节点的下标关系

假定堆的各节点数值组成一个数组，即根节点为a[0]，那么a[i]节点的2个子节点下标是什么呢？

关系如下：

j = 2 * i + 1

下文我们简要推导一下，了解这点知识的朋友可跳过此小节。

第1层只有根节点，共1个节点，即 1=2^1-1；
第2层有2个节点，即 2=2^2-1；
第3层有4个节点，即 4=2^3-1；
……
根据堆的特性，我们可以推测出：
第n-1层，该层节点共有2^(n-1)-1；
第n层，该层节点共有2^n-1；

在上图中，i 为父节点的下标，其左子节点下标为 j 。
那么根据堆（完全二叉树）的特性，最后一层的叶子节点从左向右紧密排列，之间没有空缺。因此，如果我们假定 i 左边有 x 个兄弟节点，那么显然， j 左边就有 2x 个兄弟节点。

我们来用算术式表示第n层的 i 在整个堆中的位置，即有：

式子A：i + 1 = 2^1-1 + 2^2-1 + 2^3-1 + …… + 2^(n-1)-1 + x + 1;

同理，第n+1层的 j 在整个堆中的位置为：

式子B： j + 1 = 2^1-1 + 2^2-1 + 2^3-1 + …… + 2^(n-1)-1 + 2^n-1 + 2x +1 ;

两个式子左边 +1是因为 i j 为下标，下标从0开始，因此表示位置要 +1，例如根节点在数组中的下标为0，但其位置是1。

式子 B - 2*A，右边消除相同式子。可以算出：

j = 2*i + 1

即：父节点 i 的左子节点下标为 2i+1，右子节点下标为 2i +2。

图解堆的构建

讲了这么多说明，那么对于给定的一个序列，如何构建堆呢？构建后又如何排序呢？

构建堆

依然以图解来说明其详细过程。假定对于给定的一个无序数组{6, 8, 9, 7, 2, 5, 1, 3}，我们要对其从大到小排序，那么，我们首先要对其构建最小堆，令其最小值浮到根节点。

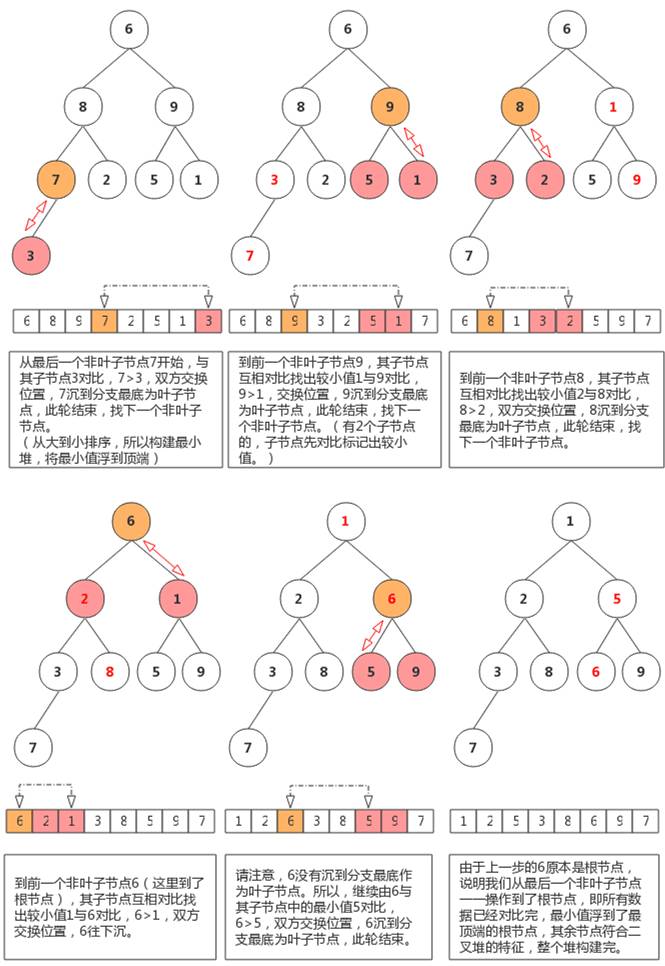
根据以上步骤，我们构建了一个堆，此时数组变成了{1, 2, 5, 3, 8, 6, 9, 7}。

在图解中，我们多次提到了从最后一个非叶子节点开始往前调整。

那么，在堆中，最后一个非叶子节点的下标或位置又是什么呢？是否有什么规律呢？

我们假定 i 为堆中最后一个非叶子节点，也就是说 i 右边及下层都是叶子节点，i 右边的节点不可能有子节点了，即 i 节点的子节点是整个堆中的最后节点。

如果 i 仅有1个子节点，那么 左节点 j 就是堆中最后一个叶子节点，即堆长度为

len = j+1 = (2i+1) +1 = 2i + 2，即 i = (len-2)/2；

（j 是下标，所以计算长度要 +1）

如果 i 有2个子节点，那么最后一个节点就是 j 右侧那个节点，即堆长度为

len = (j + 1)+1 = 2i+3，即 i = (len - 3)/2。

（j 是下标，所以计算长度要 +1）

因此，我们在调整堆时，需要分别根据堆的长度为偶数还是奇数判断最后一个非叶子节点的位置。

不过，分两个条件写有点繁琐，能否长度不论为偶数奇数就只用一个条件就可以表示2种情况呢？即无论奇数偶数，该式子所求出的 i 值都是相同的，指向的最后一个非叶节点相同。

在同一个父节点时，只有左节点长度为偶数，含有左右节点长度为奇数，也就是这里所说的长度：如果是奇数，永远会比偶数大1。

在上面的前提下，我们来分析一下。

假设只用第二个式子 i = (len-3)/2。根据int类型整除向下取整的特性，当长度为奇数时，该式等同于 i = len / 2 - 1；当长度为偶数时，该式等同于 i = len / 2 - 2。两种情况时 i 的结果不同，指向的非叶子节点不是最后一个非叶子节点，有一种情况会指向前一个非叶子节点，那么此时最后一个非叶子节点就无法参与排序，因此不能用第二个式子来代替奇偶两种情况。

假设只用第一个式子 i = (len-2)/2。当长度为奇数时，该式等同于 i = len /2 -1；当len为偶数时，该式等同于 i = len / 2 -1。两种情况指向的 i 是相同的，即指向的最后一个非叶子节点是正确的。

因此，最后一个非叶子节点的下标，我们统一标记为 i = (len-2)/2，这个点也是堆调整的起始点，之后每调整完一个值，就往前找另一个非叶子节点，即 a-- 自减。

构建堆的代码表达

根据图解中构建堆的大致过程，我们尝试用代码方式来表达。

   public static void buildHeap(int[] a) {
       // 从最后一个非叶子节点开始
       for (int i = (a.length -2)/ 2; i >= 0; i--) {
           heapAdjust(a, i, a.length);//每次的非叶子节点自减1
       }
   }

   //调整堆
   private static void heapAdjust(int[] a, int parent, int length) {
       int temp = a[parent]; //temp保存当前非叶子/父节点的值
       int child = 2 * parent + 1; //左节点下标 j=2i+1

       while (child < length) {
           // 左右节点对比，标记值小者
           if (child + 1 < length && a[child] > a[child + 1]) {
               child++;
           }

           // 如果父结点的值已经小于等于孩子结点的值，无法下沉，说明已到合适位置
           if (temp <= a[child])
               break;

           // 否则，把子节点值放在父节点，将子节点当成父节点继续向下沉
           a[parent] = a[child];
           parent = child;
           child = 2 * child + 1;
       }

       //将初始的非叶子节点值赋值给当前的节点
       a[parent] = temp;
   }

图解堆排序

接下来依然用图解的方式将堆排序的过程详细画出，不过刚才的数组长度为8位，用图解方式画出来比较占篇幅而且重复、累赘，我们这里用一个稍短一些的有堆特性的5位长度数组来演示。

数组从刚才那个构建好堆的数组中截取前4位。

（看图会发现，前任意n位元素，其实就是堆中的前n个节点。所以此处截取前任意n个的元素组成新数组，都是符合堆特性的。）

数组为：{1, 2, 5, 3}。

从图解中可以看出，在一个已调整好的二叉堆中，排序的整体思路是将首尾的值进行了交换，将最小值取出放入数组末位，此时根节点的值可能不符合最小堆的特性，因此需要将其和子节点中的小值对比往下沉，直到沉到合适位置……此时二叉堆又调整好了，开始新一轮的取出……

我们依然尝试用代码来表达……

public static void sortHeap(int[] a){
  int temp;

  //从数组末位下标开始，每循环一次，长度-1，直到只剩1个节点
  for(int i=a.length-1; i>0;i--){

     //交换首尾值
     temp = a[0];
     a[0] = a[i];
     a[i] = temp;

     //每次从根节点开始调堆，长度为i（因为每排好1个就无视1个节点）
     heapAdjust(a, 0, i);
  }
}

核心代码

我们整理一下上文的代码，堆排序算法如下：

public static void heapSort(int[] a){
   buildHeap(a);//构建二叉堆
   sortHeap(a);//堆排序
}

private static void buildHeap(int[] a) {
   // 从最后一个非叶子节点开始
   for (int i = (a.length -2)/ 2; i >= 0; i--) {
       heapAdjust(a, i, a.length);//每次的非叶子节点自减1
   }
}

private static void sortHeap(int[] a){
  int temp;

  //从数组末位下标开始，每循环一次，长度-1，直到只剩1个节点
  for(int i=a.length-1; i>0;i--){

     //交换首尾值
     temp = a[0];
     a[0] = a[i];
     a[i] = temp;

     //每次从根节点开始调堆，长度为i（因为每排好1个就无视1个节点）
     heapAdjust(a, 0, i);
  }
}

//调整堆
private static void heapAdjust(int[] a, int parent, int length) {
   int temp = a[parent]; //temp保存当前非叶子/父节点的值
   int child = 2 * parent + 1; //左节点下标 j=2i+1

   while (child < length) {
       // 左右节点对比，标记值小者
       if (child + 1 < length && a[child] > a[child + 1]) {
           child++;
       }

       // 如果父结点的值已经小于等于孩子结点的值，无法下沉，说明已到合适位置
       if (temp <= a[child]){
           break;
       }

       // 否则，把子节点值放在父节点，将子节点当成父节点继续向下沉
       a[parent] = a[child];
       parent = child;
       child = 2 * child + 1;
   }

   //将初始的非叶子节点值赋值给当前的节点
   a[parent] = temp;
}

纯文笔记

记录知识，分享心得。