二叉堆和堆排序（binary heap）

Posted 2021-05-01 秀觅code

• 什么是二叉堆

     

        二叉堆是一种特殊的二叉树。二叉树是每个节点只有两个子节点的树（应该都懂吧）。二叉堆分为两种：最大堆和最小堆，最大堆的父节点一定大于其子节点（根节点最大），最小堆的父节点小于其子节点（根节点最小）。

下面是一个二叉树：

         我们用一维数组将二叉树初始化，例如：我们有{1，2，3，4，5，6，7}七个数要放入堆中，第一步初始化数组的长度为8，array[0]为null，array[1]~array[7]放入数字。

          为什么array[0]为null呢？因为要用下标值找到它的子节点和父节点，比如a[1]=1,a[2]=2,a[3]。我们知道a[1]的子节点是a[2],a[3],由于是二叉树，a[k]的子节点一定是a[2k]和a[2k+1],a[k]的父点一定是a[k/2]。花个20秒思考一下吧。

         图示：

             

                           

          

                  

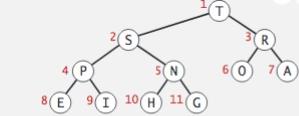
• 将一个二叉树变成二叉堆

       

          我以最大堆为例，最大堆的定义是：父节点的value一定要大于子节点的             value。

          1.  子节点的value大于父节点的value的情况

              

          此时T大于P，违反了最大堆的平衡性，所以要将T和其父节点对调

              

                           

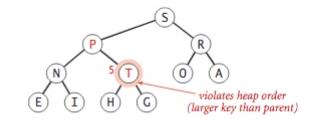
        但是T移动到了P的位置后，它的值依然比其父节点要大，还要上浮

                      

                                 

         

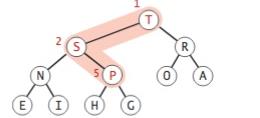
        最终T移动到了根节点，最大堆平衡了

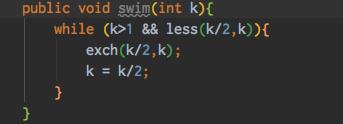
代码swim（名字起的真的很赞）

         

          

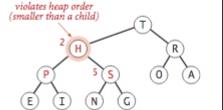
        2.  父节点的value小于子节点的value的情况

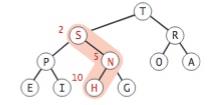
          此时，H比子节点要小，H要下沉，先比较P和S谁比较大，跟大的换位置

             

           

                              

          

          跟S换之后，发现依然比子节点要小，还是要下浮，最后

           

                               

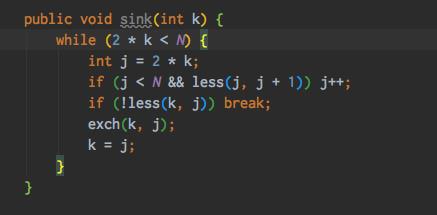
    代码sink：

        

                

• 上浮和下沉的作用，即第二部分的应用

       

1. 向数组插入value会用到上浮    

   
   

       每次向队尾插入一个value时，都要检查是否违反最大堆的平衡性。





        

                    

       

  b.   删除根节点时，会用到下沉

         

            每次想删除根节点，第一步是要将跟节点与最后一个节点互换位置后，将其删除，此时最后一个节点作为根节点，一定会比子节点要小，违反平衡性，那就下浮

      

          

                      




•     堆排序（简单提一提）

                

    很简单，最大堆为例，根节点是最大的节点，那就每次将根节点删除，待其最大堆再次平衡时，再将根节点删除，即为排序。代码不贴了，有兴趣可以自己尝试一下。