简易学算法之堆排序

Posted 2021-05-01 硬件工程师的自我修养

（请戳：  

因为昨天所介绍过选择排序，而堆排序是属于选择排序的一种，且效率更加高效，是普通选择排序的“升级版”！

相信有了昨天的简单选择排序的铺垫，堆排序估计不难！

可是等到要写才发现，如果要通过代码来讲解，那确实有些困难，而且我也还没有完全地理解代码方面的解析，就不好写出来了。

诚然，我目标是以个人理解到什么程度，然后写出来，大家看完之后，也能够达到我这个理解效果，我是一个老实的人！

“我用完之后是这个样子，而你们用完之后也会是这个样子！”

   ——国际知名影视巨星 成龙

难点关键在于这个“堆”字。

因为介绍“堆”需要用到有关“二叉树”的知识来解释...但用一篇文章来解释就有些不适合。我想，一篇文章只需要介绍一个知识点就够了，我是一个专一的人！

其实一般人也不需要怎么用到树的啦，又不是人人需要写程序，了解一下算法的思想就够了（没错，“二叉树”打算是作为与本篇 “堆排序”的接下来姐妹篇）

总之，先用图片介绍一下，同样是先有一个感性的认识吧。因为我是从这些图片理解了“堆排序”是怎么工作的。

来人，上图片！

遇到问题

有以下数列

91, 60, 96, 13, 35, 65, 46, 65, 10, 30, 20, 31, 77, 81, 22

请由小到大排列

堆排序

待排列的数列

先把这一排的数列，转换成堆。下图这个叫做 大顶堆：

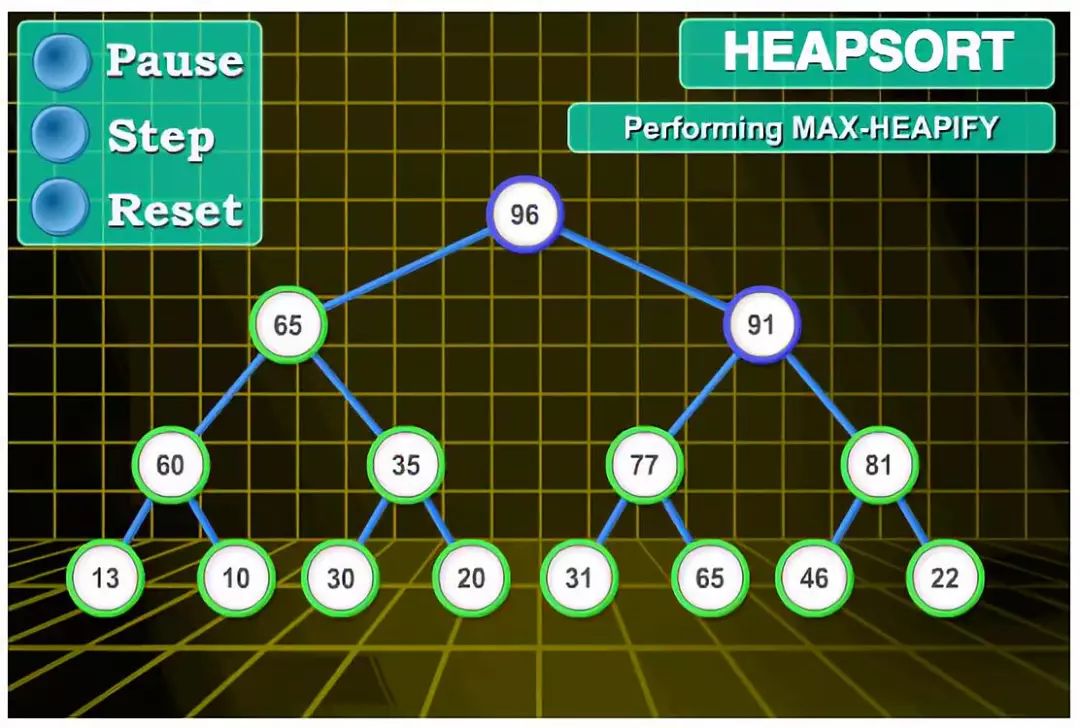
之所以称为“大”，是因为每一个节点（父节点）都比下面的分支（子节点）的数字要大。

如： 父节点 96，比其子节点 65和91大；父节点65，比其子节点60和35大。

相反地，我们也会有小顶堆，那是用来从大到小排列时用的。

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右子结点的值，称为小顶堆。

接下来开始排列，动起来，动起来：

好了，大概有点感性理解了没？我又专门地画一些简单的图呢！

进入最大堆；我可以看到最大堆里顶点肯定是数列中最大的一个，96。

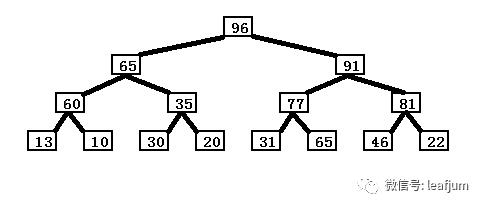
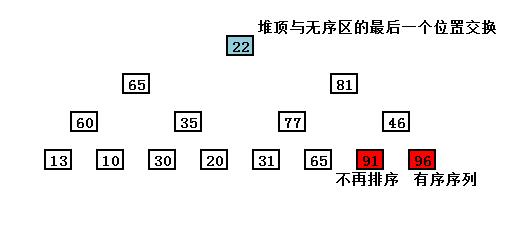
把顶点96和最底层最右边的子节点22交换。

（这里注意一下，堆只是说明父节点比子节点要大，至于两个子节点之间的大小、子节点与其他层级的节点大小无关，因此堆初始最右边放的并不是最小的值，如图是 22，并不是最小值）

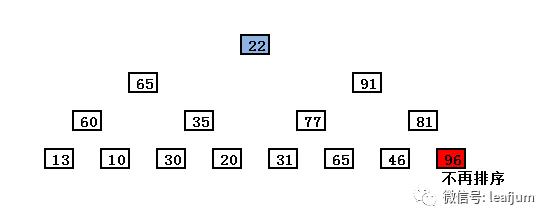
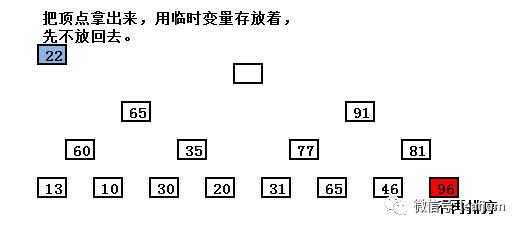
由于有空位，两个子节点 65 和 91 对比，91大，所以91成为父节点，顶上去！

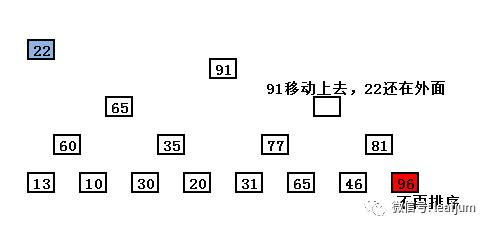
由于91移动上去，其下面的子节点要补充空位，同样把大的子节点移动上去。

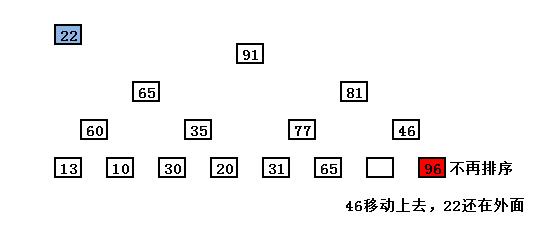
最后，22归位，补充空缺，这样就完成了一趟排序！堆也成为一个新的堆。

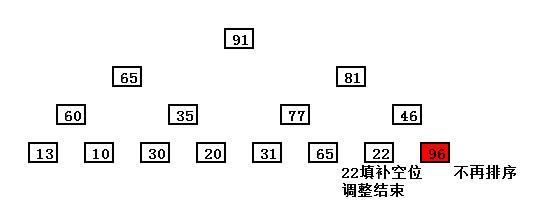
红色的数96，表示已经排列完成的数了，不再参与排序。它是属于“有序排列”，而白色的数是叫做“无序排列”。

那什么是有序排列、无序排列呢？在上一篇： 

里介绍选择排序有这么一出：

其中，大括号{ }外面的数，就是“有序排列”，括号里面的数就是“无序排列”。（这么说来，难怪这么奇葩的堆排序也称为是属于选择排序的一种了。）

上面的第一趟完成后，我们再重复开始第二趟！按照先前的步骤，交换堆顶与最后一个位置...如此循环直到所有数字成为有序排列。

得到最后答案 有序序列：

遗留问题

最后，相信大家心里是隐隐作痛，我怎么知道开始把一个一维数列，变化成为一个大顶堆，然后才开始这么排序啊！这就是我文中一开始所提出的难题啦。而本篇至少让我们明白了堆排序是怎么进行的了！

哒哒哒哒

至于关于数列转化堆这个疑问，就交由下一姐妹篇，“二叉树”篇来说明吧！