基础算法六之堆排序
Posted IT小码哥
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基础算法六之堆排序相关的知识,希望对你有一定的参考价值。
前言
曾经一度不想继续下去了,各种理由都是借口,惰性已经侵占了我,一回家,我就趟床上睡觉了,并没有按计划进行写作,心里确实很惭愧。希望大家监督,以后每天即使很晚都要完成自己定的目标,每周完成四篇原创算法文章。(已经有一周多没更新了,愧对为自己打气的小伙伴)
接下来将和大家一起进入堆排序的世界。
· 正 · 文 · 来 · 啦 ·
堆排序
首先了解几个概念:
普通队列:先进先出,后进后出
优先队列:出队顺序和入队顺序无关,和优先级相关
堆就是优先队列
二叉堆是一颗完全二叉树(最大堆:堆中某个节点的值总是不大于其父节点的值,堆总是一颗完全二叉树。反之最小堆定义),如下图
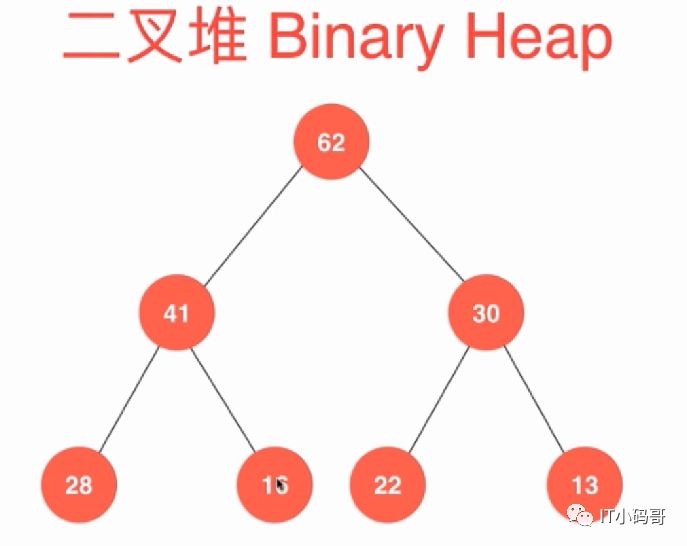
操作堆的过程中需要进行入队出队操作,所谓入队就是插入元素,出队就是选择优先级最高的元素。
普通数组,入队,也就是添加元素,时间复杂度为0(1),但是出队就需要比较了元素大小,复杂度为O(n),顺序数组入队则是O(n),出队则是O(1),堆入队出队都是O(㏒ n)。
首先定义一个MaxHeap类,模拟堆操作。但这之前需要知道左右孩子节点和父节点的关系,通过下图将一目了然
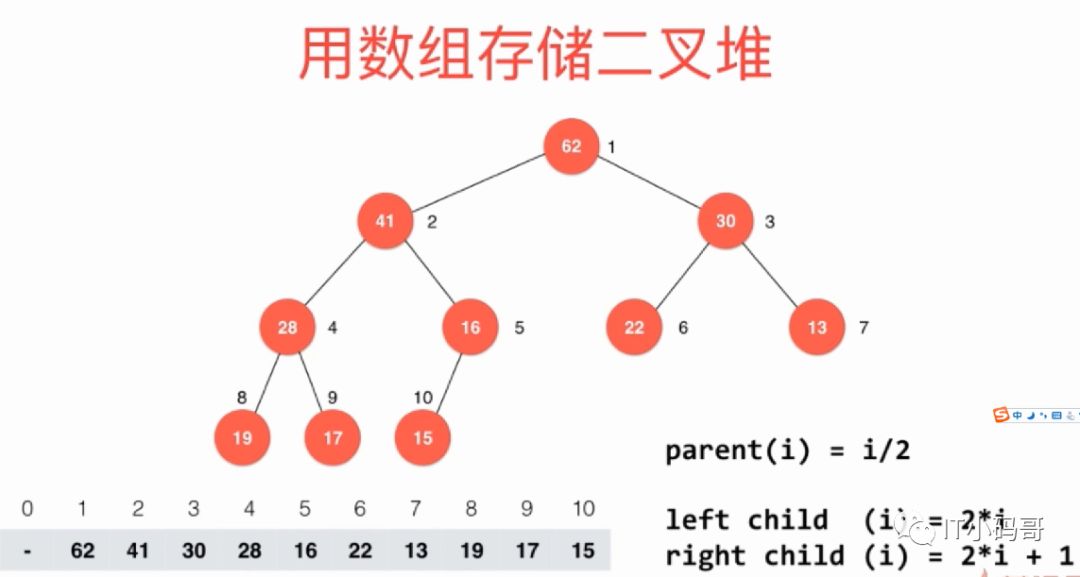
这里是从下标1开始存储的,包括代码实现都是从下标1开始记录的。一般情况都是从0到n-1为数组下标存储数据,如果从0开始存储则parent(i) = (i-1)/2,left child = 2*i+1 , right child = 2*i+2
下面则是MaxHeap类的具体实现与讲解。
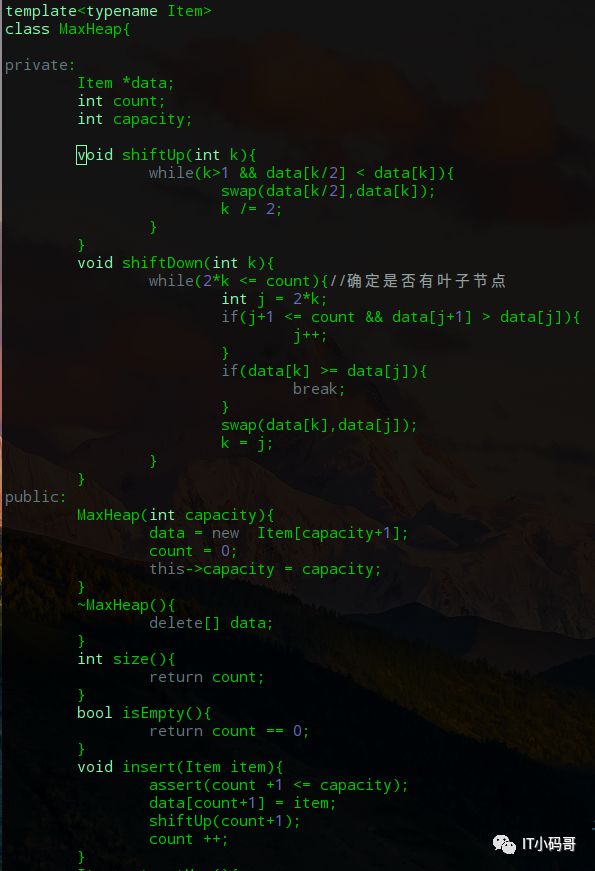
data是存储的数据数组,当每添加一个元素,count就加1,capacity是数组元素大小,因为data中是1到n存储数据,所以数组大小要多加1
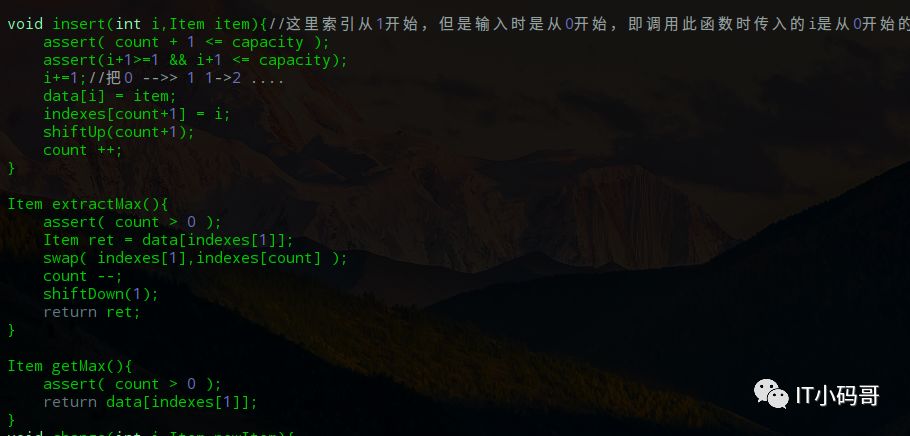
其中insert()函数是添加元素到堆中,每添加一个元素就需要执行该位置节点上的shiftUp操作
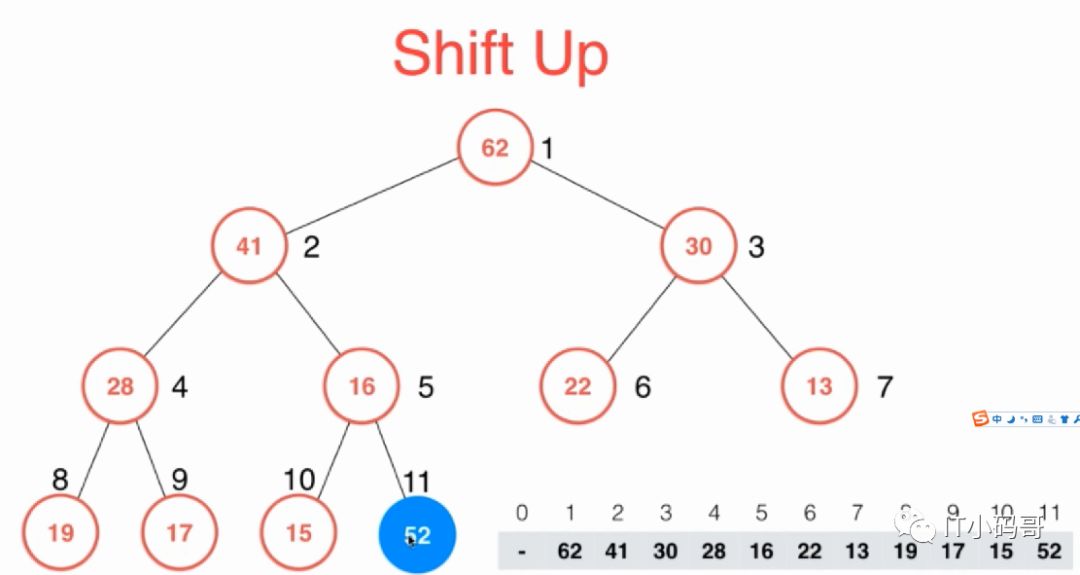
例如添加52这个元素,则需要将11节点上的52与5节点上的16比较,52大,则交换值并和2节点的41比较,一步一步往上进行比较,使得继续满足最大堆性质(本文都是基于最大堆实现的)。
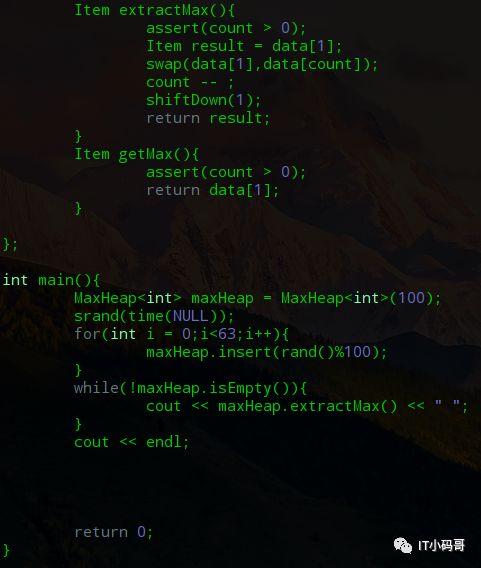
当执行出队操作时,就需要调用exractMax()将堆顶元素,即最大元素取出来,然后将最后一个叶子节点上的元素放到堆顶,执行shiftDown操作
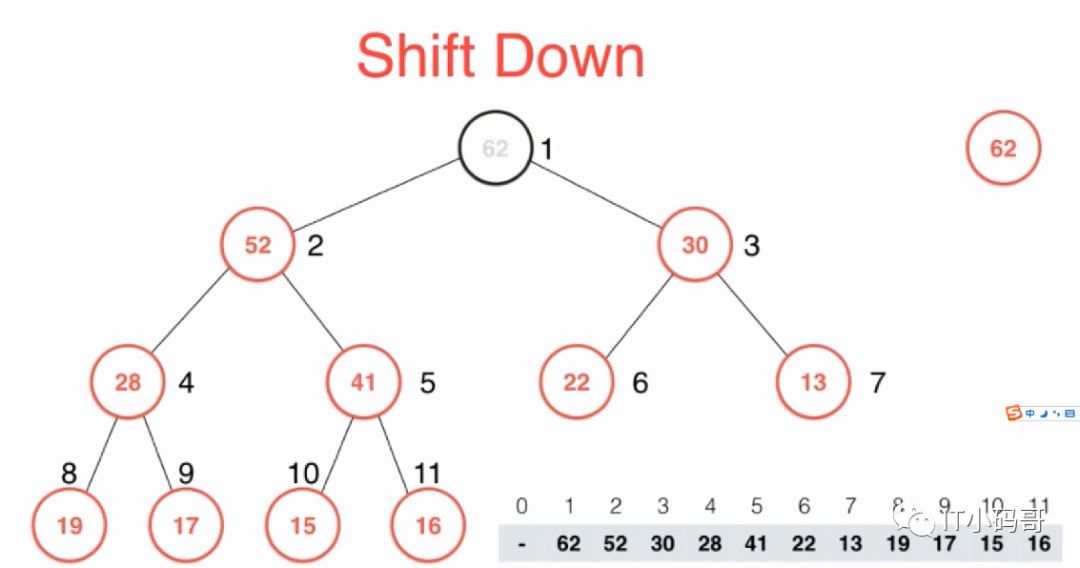
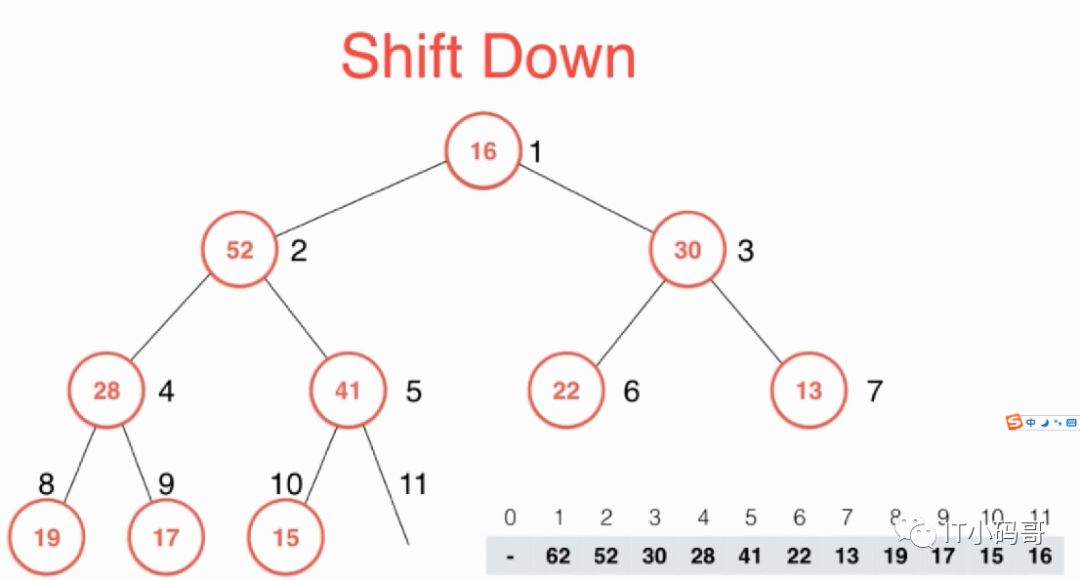
如上图,取出最大元素62后,把最后一个元素16放到堆顶,然后将此元素与直接子节点最大值比较,保证父节点元素大于两个子节点,依次往下操作,这就是shiftDown操作。
这里主要是排序,不进行删除等操作,所以仅仅实现了堆的插入和取出操作,有兴趣的读者可以完善。
利用堆的性质,入队和出队操作,可以实现堆一个数组进行排序,先将每个元素插入到堆中,然后取出每个元素,得到的数组即是排好序了的。
实现方法很简单,调用MaxHeap的insert方法,然后在调用extractMax方法即可。代码实现如下图的heapSort1方法
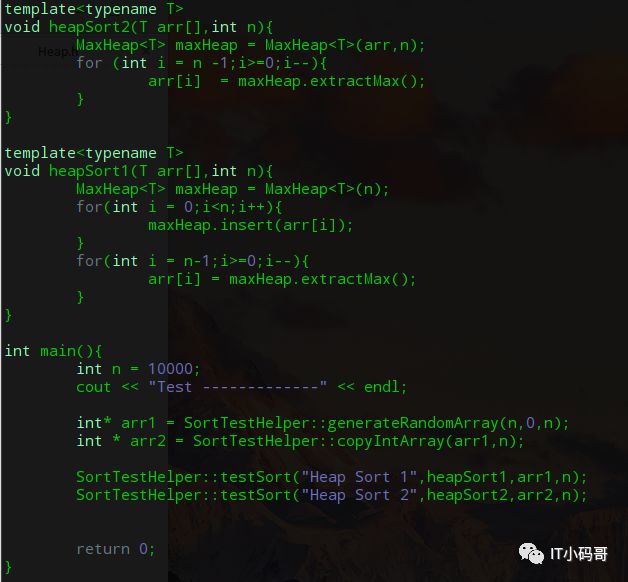
但是大家注意到没,heapSort1方法内是将一个个元素插入构成最大堆,我们可不可以直接将数组传入构建成最大堆呢,当然是可以的,例如上面的heapSort2方法,因为对用户或者调用者来说,无疑是我把一个集合给你,然后内部自动构建成堆的形式比较好。其中添加的构造方法如下,从第一个非叶子节点开始,执行shiftDown操作构建堆。
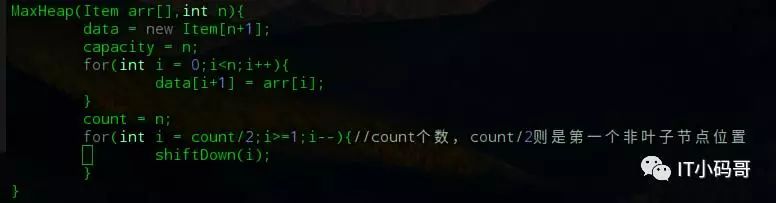
最重要的是heapSort2()这样构建堆,它的复杂度是O(n),而heapSort1()将元素插入到空堆中复杂度是O(n㏒ n)。所以尽量采用第二种方法进行排序。
堆排序的简单操作已经实现了,仔细的读者会发现,每次排序都要将数组的元素放到堆中,这样是不是会浪费内存呢,有没有方法进行原地排序呢?答案肯定是有的。我们可以先找到第一个非叶子节点元素,然后执行shiftDown操作。注意,这里是直接操作数组,所以下标从0开始,所以k位置如果是第一个非叶子节点,则2 × k + 1是该节点的左孩子的位置,这个值得小于数组大小。
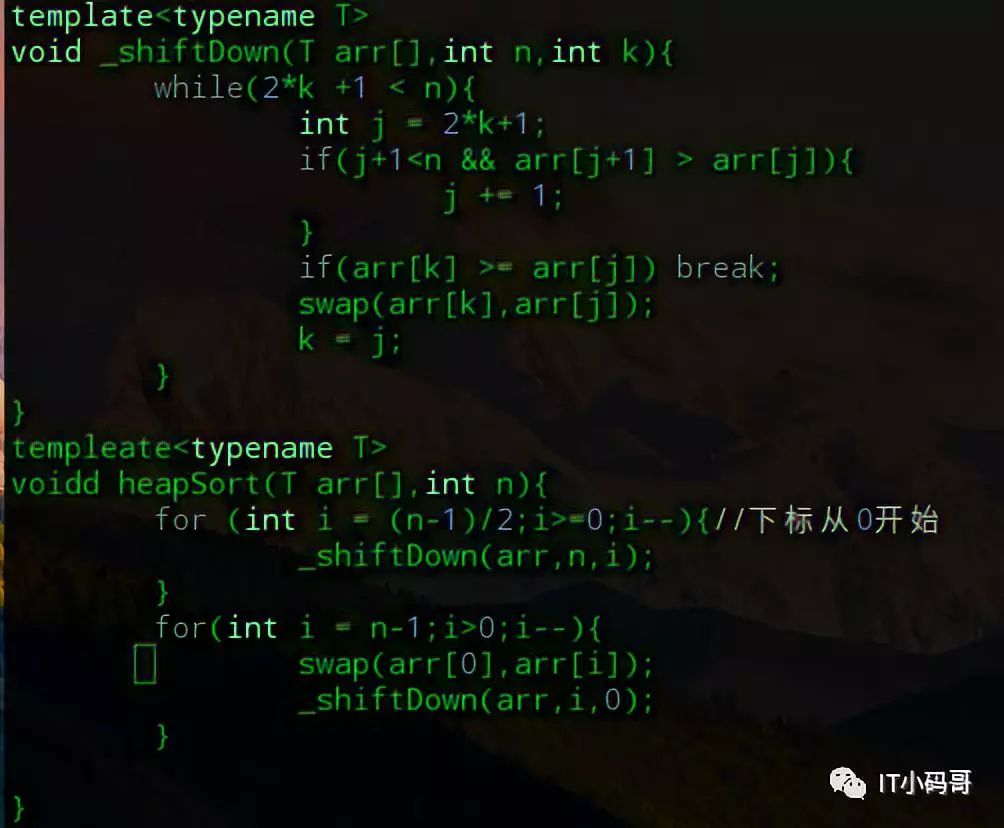
执行完第一个循环后,数组是最大堆形式。但是我需要将数组从小到大排序,所以就需要每次都将第一个元素和最后一个元素交换值,然后再将堆顶元素进行shiftDown操作。有人可能会说,我从头开始设计成最大堆不可以么,哪有这么费事,当然可以,但是需求总是突如其来的,最好的方法是将堆构建成以最大堆和最小堆共存的形式,然后提供给别人使用,想怎么用就怎么用。
在之前讲解插入排序时,将结果如何简化swap(arr[k],arr[j])这个步骤,不知道还记得么,这里再重新提一下,我们可以每次将需要shiftDwon的元素值先保存起来,找到最后需要放置的节点位置后,赋值。这样就避免了开辟一块新空间来交换值。
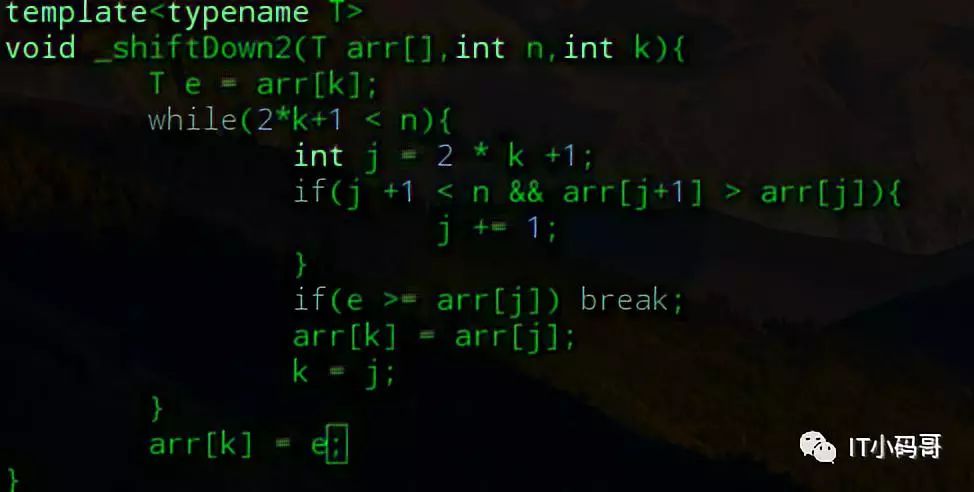
大家有没有想过,如果交换的元素是字符串或者其他复杂的结构,那这样每一次交换都会消耗不小的空间。
那怎么办呢,于是索引堆就出现了,每次我都交换索引岂不是妙哉。
接下来就需要改一下MaxHeap类了,只需要将之前元素下标的位置替换成索引数组的对应值就可以了,维护索引堆即可。
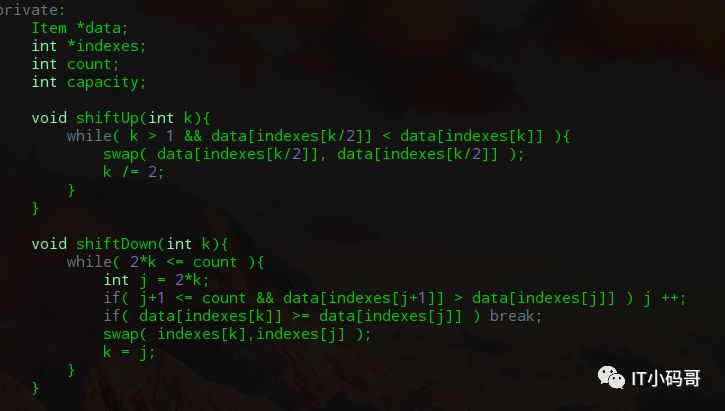
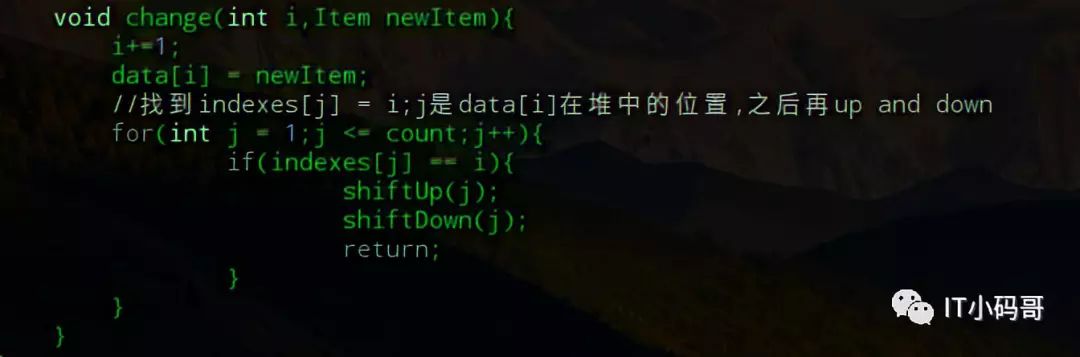
总结
当你看完了这篇堆排序,是不是觉得很简单。只要记住堆是一种完全二叉树,还有最大堆和最小堆的性质,根据这个基本就能写出来。
建议有时间的读者将前面几篇排序手写出来,这样理解得将会更深。
最近看到有个公司的面试题:
请写一段代码合并下面两个有序数组,要求输入{1,5,9,11,17}和{4,15,23,27,44},输出为{1,4,5,9,11,15,17,23,27,44},并写出所用的时间复杂度和空间复杂度。
分析:合并数组,取最小的元素放到新集合中,相同元素只放一个。
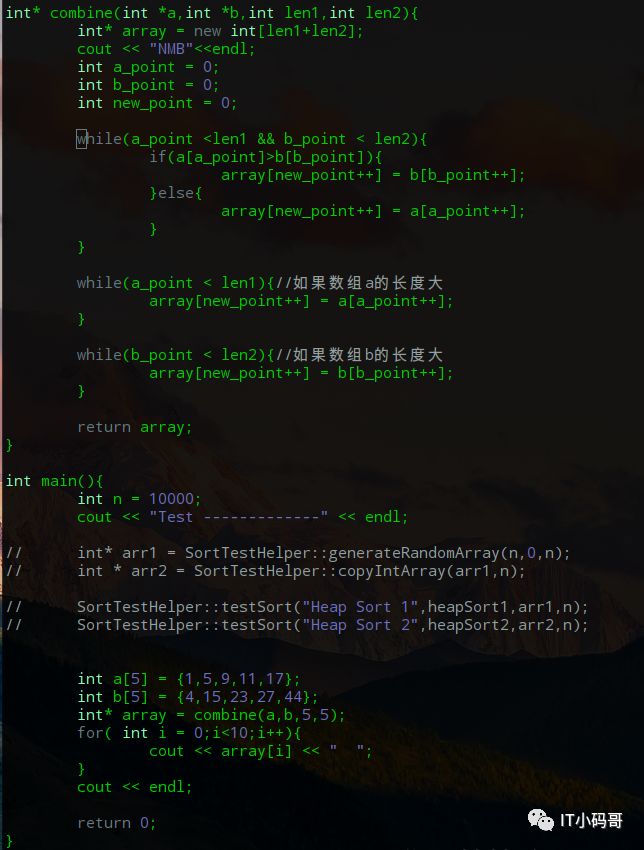
这里数组长度大家可以自行设置,时间复杂度O(m+n),辅助空间O(m+n),这样做并不是最优的,在上述问题中,完全可以根据a,b数组,谁的元素多用谁替换combine中定义的array,实现空间复杂度为O(1)。


欢迎大家关注
欢迎大家在后台回复『加群』或者点击『读者群』加入群一起交流

以上是关于基础算法六之堆排序的主要内容,如果未能解决你的问题,请参考以下文章