最大堆(创建删除插入和堆排序)
Posted BigData大数据分享
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最大堆(创建删除插入和堆排序)相关的知识,希望对你有一定的参考价值。
> 本文共计 7643 字,阅读时间大概 13 分钟。
关于最大堆
什么是最大堆和最小堆?
最大(小)堆是指在树中,存在一个结点而且该结点有儿子结点,该结点的data域值都不小于(大于)其儿子结点的 data 域值,并且它是一个『完全二叉树』(不是满二叉树)。
完全二叉树(Complete Binary Tree):除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。
下面列举了几个最大堆的图片,也可以更好的辨析何为完全二叉树。
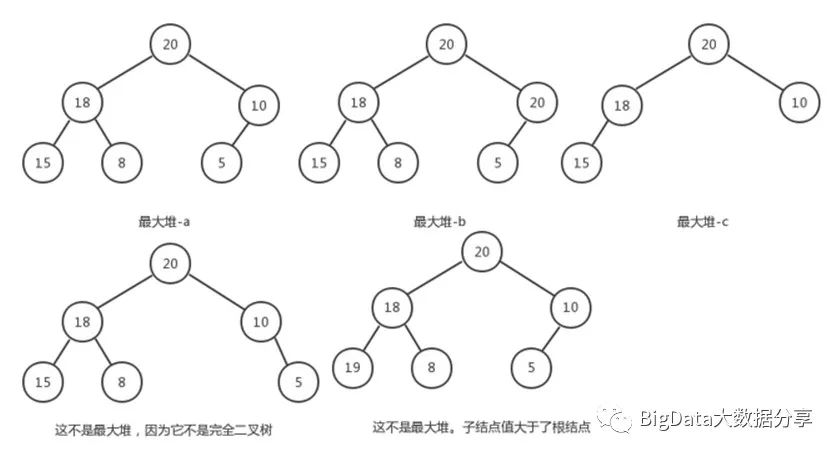
注意:最大堆中,根结点大于其它任意的子结点,并且是一个完全二叉树结构。
最大堆ADT
其抽象数据类型(ADT)需要考虑三个操作:
(1)、创建一个最大堆;
(2)、最大堆的插入操作;
(3)、最大堆的删除操作;
在最大堆中,不管是插入还是删除操作,我们都需要考虑如何维护这个最大堆,在插入还是删除之后,仍然还是一个『完全二叉树』。
最大堆在内存中有两种表现形式:
第一种方式,我们使用链表的方式来实现。(暂不考虑)
第二种方式,使用『数组』实现,在二叉树进行遍历的方法分为:先序遍历、中序遍历、后序遍历和层序遍历。我们可以通过层序遍历的方式将二叉树结点存储在数组中,由于最大堆是完全二叉树,不会存在数组的空间浪费。
比如,对下面的堆进行『层序遍历』。
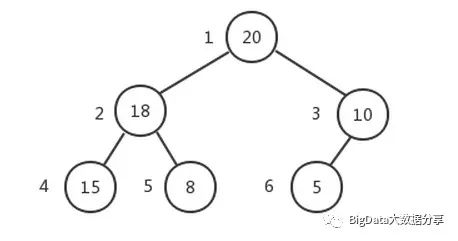
其中需要注意的是,我们的编号从 1 开始。层序遍历的流程变化如下:
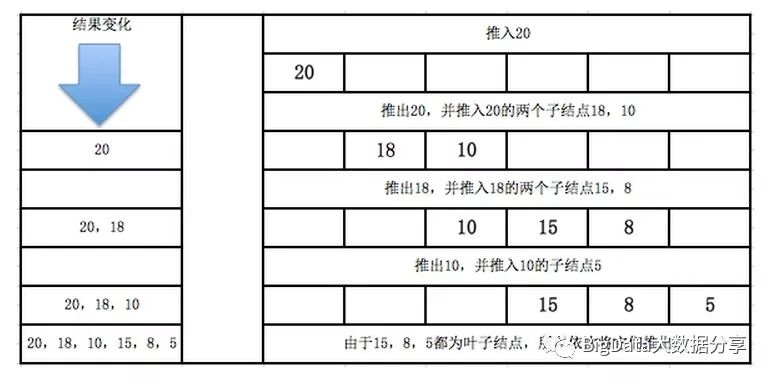
层序遍历的过程可以参考队列的思想『先进先出』。
上表中对应的内容和二叉树的内容是一致的。
那么对于数组我们怎么操作父结点和左右子结点呢?对于完全二叉树采用顺序存储表示,那么对于任意一个下标为i(1 ≤ i ≤ n)的结点:
(1)、父结点为:i / 2(i ≠ 1),若i = 1,则 i 是根节点。
(2)、左子结点:2i(2i ≤ n), 若不满足则无左子结点。
(3)、右子结点:2i + 1(2i + 1 ≤ n),若不满足则无右子结点
最后存储的的数据结构如下:
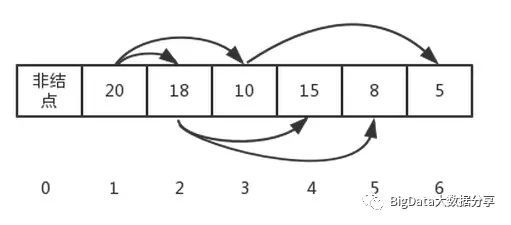
最大堆的插入
最大堆的插入,可以简单的看成是结点的『上浮』。当我们在向最大堆中插入一个结点我们必须满足完全二叉树的标准,那么被插入结点的位置的是固定的。而且要满足父结点关键字值不小于子结点关键字值,那么我们就需要去移动父结点和子结点的相互位置关系。具体的『最大堆插入』位置变化,可以看看下面的一个简单的图。
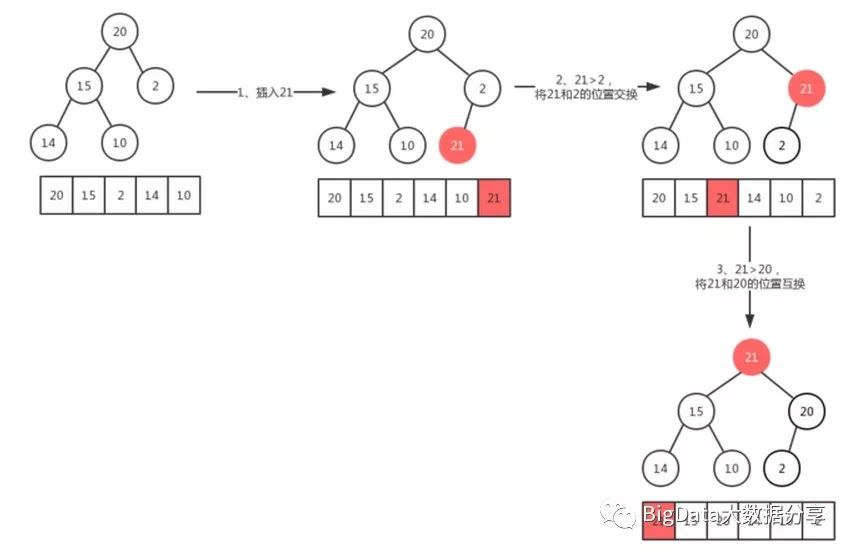
由于堆是一棵完全二叉树,存在n个元素,那么他的高度为:log2(n+1),这就说明代码中的for循环会执行O(log2(n))次。因此插入函数的时间复杂度为:O(log2(n))。
代码实现:
/** * 插入一个元素到heap中,插入一个数字,实现结点上浮 * * @param data 插入的数据 */ public void insertValue(int data) { int len = heap.length; int[] newArray = new int[heap.length + 1]; System.arraycopy(heap, 0, newArray, 0, len); newArray[len] = data; int index = len; while (index >= 1) { fixValue(newArray, index, newArray.length); index = index >> 1; } heap = newArray; }
最大堆的删除
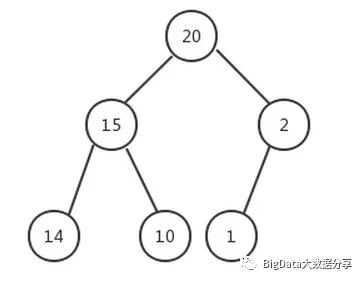
最大堆的删除操作,总是从堆的根结点删除元素。同样根元素被删除之后为了能够保证该树还是一个完全二叉树,我们需要来移动完全二叉树的最后一个结点,让其继续符合完全二叉树的定义,从这里可以看作是最大堆最后一个结点的下沉(也就是下文提到的结点1)操作。例如在下面的最大堆中执行删除操作:
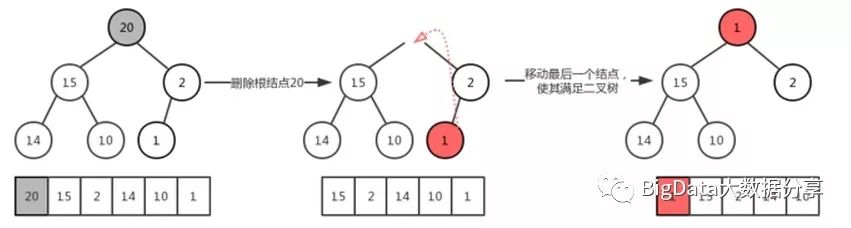
第一步,我们删除上图中的根结点
20;当删除根结点
20之后明显不是一个完全二叉树,更确切地说被分成了两棵树。我们需要移动子树的某一个结点来充当该树的根节点,那么在(15,2,14,10,1)这些结点中移动哪一个呢?显然是移动结点 1,如果移动了其他结点(比如14,10)就不再是一个完全二叉树了。
对上面三步图示如下:
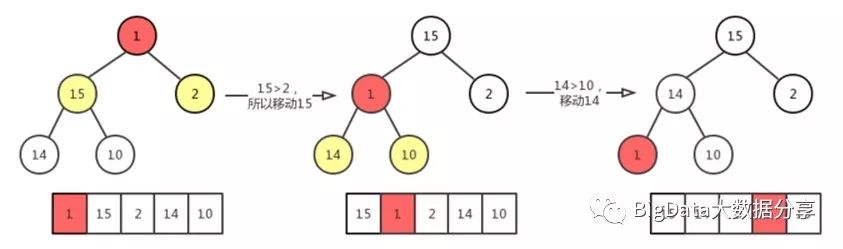
显然现在看来该二叉树虽然是一个完全二叉树,但是它并不符合最大堆的相关定义,我们的目的是要在删除完成之后,该完全二叉树依然是最大堆。因此就需要我们来做一些相关的操作!
1)、此时在结点(15,2)中选择较大的一个和 1 做比较,即 15 > 1 的,所以 15 上浮到之前的 20 的结点处。
2)、同第 1 步类似,找出(14,10)之间较大的和 1 做比较,即 14 > 1 的,所以 14 上浮到原来 15 所处的结点。
3)、因为原来 14 的结点是叶子结点,所以将 1 放在原来 14 所处的结点处。
同最大堆的插入操作类似,同样包含n个元素的最大堆,其高度为:log2(n+1),其时间复杂度为:O(log2(n))。
总结:由此可以看出,在已经确定的最大堆中做删除操作,被删除的元素是固定的,需要被移动的结点也是固定的,这里我说的被移动的元素是指最初的移动,即最大堆的最后一个元素。移动方式为从最大的结点开始比较。
代码实现:
void delete() { // 先把最末尾的元素放入到首 int len = heap.length; int[] newArray = new int[len - 1]; swap(heap, 1, len - 1); System.arraycopy(heap, 0, newArray, 0, len - 1); int index = 1; while (index < len - 1) { int nextIndex = downValue(newArray, index, len - 1); index = nextIndex; } heap = newArray; } /** * 下沉 * * @param array * @param i * @param len * @return */ int downValue(int[] array, int i, int len) { int left = 2 * i; int right = 2 * i + 1; if (right < len && array[right] > array[i]) { swap(array, i, right); return right; } if (left < len && array[left] > array[i]) { swap(array, i, left); return left; } return len + 1; }
最大堆的创建
为什么要把最大堆的创建放在最后来讲?因为在堆的创建过程中,有两个方法。会分别用到最大堆的插入和最大堆的删除原理。创建最大堆有两种方法:
(1)、先创建一个空堆,然后根据元素一个一个去插入结点。由于插入操作的时间复杂度为 O(log2(n)),那么 n 个元素插入进去,总的时间复杂度为O(n * log2(n))。
(2)、将这 n 个元素先顺序放入一个二叉树中形成一个完全二叉树,然后来调整各个结点的位置来满足最大堆的特性。
{79,66,43,83,30,87,38,55,91,72,49,9}
将上诉15个数字放入一个二叉树中,确切地说是放入一个完全二叉树中,如下:
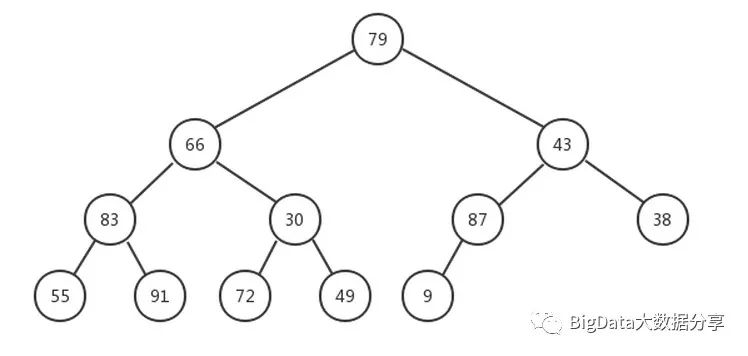
但是这明显不符合最大堆的定义,所以我们需要让该完全二叉树转换成最大堆!怎么转换成一个最大堆呢?
最大堆有一个特点就是其各个子树都是一个最大堆,那么我们就可以先把最小子树转换成一个最大堆,然后依次转换它的父节点对应的子树,直到最后的根节点所在的整个完全二叉树变成最大堆。那么从哪一个子树开始调整?
我们从该完全二叉树中的最后一个非叶子节点为根节点的子树进行调整,然后依次去找倒数第二个倒数第三个非叶子节点…
int[] heap; // 堆的数组表示 /** * 最大堆的创建,根据一个数组来创建一个最大堆 * * @param array 输入的数组 */ public void createHeap(int[] array) { int len = array.length; int[] newArray = new int[len + 1]; System.arraycopy(array, 0, newArray, 1, len); for (int i = newArray.length >> 1; i >= 1; i--) { fixValue(newArray, i, newArray.length); } heap = newArray; } /** * 调整非叶子结点的值,符合最大堆算法 * * @param array 数组 * @param i 非叶子结点的下标 * @param len 数组的长度 */ void fixValue(int[] array, int i, int len) { int left = 2 * i; int right = 2 * i + 1; if (right < len && array[right] > array[i]) { swap(array, i, right); } if (left < len && array[left] > array[i]) { swap(array, i, left); } }
具体步骤
在做最大堆的创建具体步骤中,我们会用到最大堆删除操作中结点位置互换的原理,即关键字值较小的结点会做下沉操作。
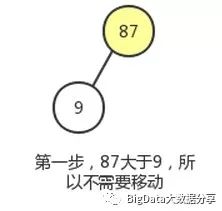
1)、就如同上面所说找到二叉树中倒数第一个非叶子结点 87,然后看以该非叶子结点为根结点的子树。查看该子树是否满足最大堆要求,很明显目前该子树满足最大堆,所以我们不需要移动结点。该子树最大移动次数为 1。
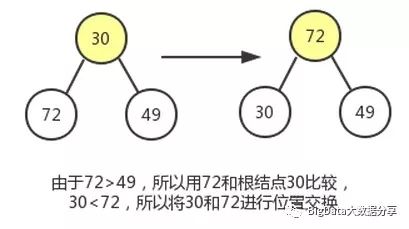
2)、现在来到结点 30,明显该子树不满足最大堆。在该结点的子结点较大的为 72,所以结点 72 和结点 30 进行位置互换。该子树最大移动次数为 1。
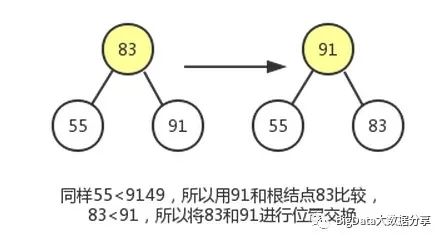
3)、同样对结点 83 做类似的操作。该子树最大移动次数为 1。
4)、现在来到结点 43,该结点的子结点有{87,38,9},对该子树做同样操作。由于结点 43 可能是其子树结点中最小的,所以该子树最大移动次数为 2。
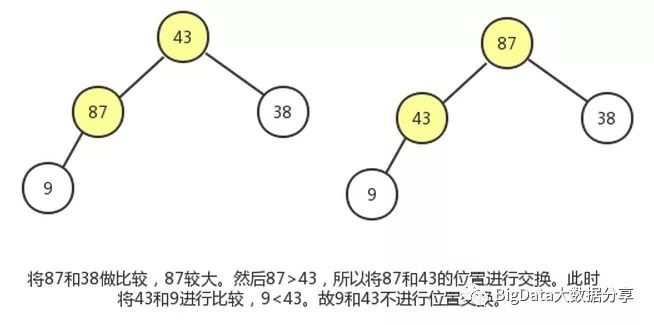
5)、结点 66 同样操作,该子树最大移动次数为2。
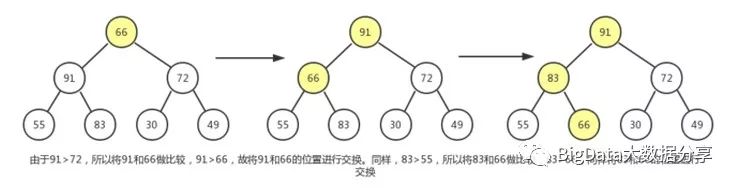
6)、最后来到根结点 79,该二叉树最高深度为 4,所以该子树最大移动次数为 3。
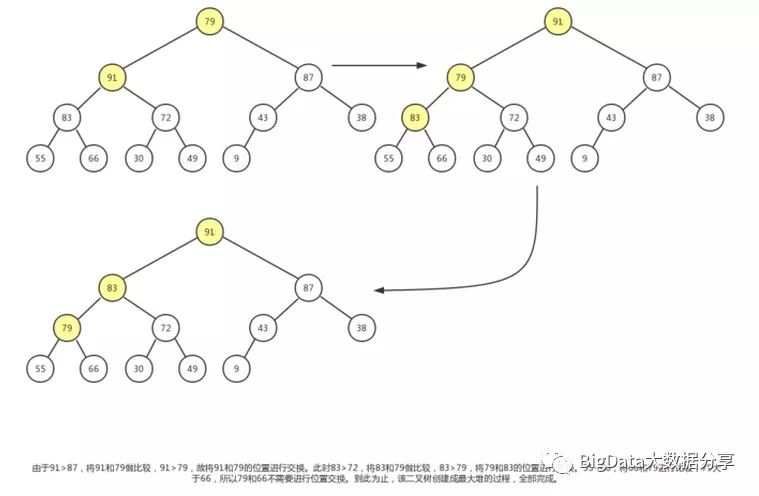
自此通过上诉步骤创建的最大堆为:
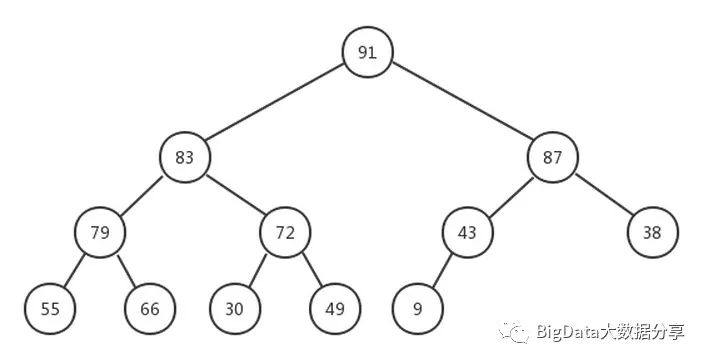
所以从上面可以看出,该二叉树总的需要移动结点次数最大为:10。
由于该完全二叉树存在n个元素,那么他的高度为:log2(n+1),这就说明代码中的for循环会执行O(log2(n))次。因此其时间复杂度为:O(log2(n))。
堆排序
堆排序要比空间复杂度为O(n)的归并排序要慢一些,但是要比空间复杂度为O(1)的归并排序要快!
通过上面最大堆创建一节中我们能够创建一个最大堆。出于该最大堆太大,我将其进行缩小以便进行画图演示。
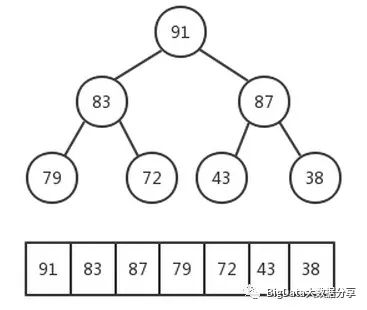
最大堆的排序过程其实是和最大堆的删除操作类似,由于最大堆的删除只能在根结点进行,当将根结点删除完成之后,就是将剩下的结点进行整理让其符合最大堆的标准。
1)、把最大堆根结点91“删除”,第一次排序图示:
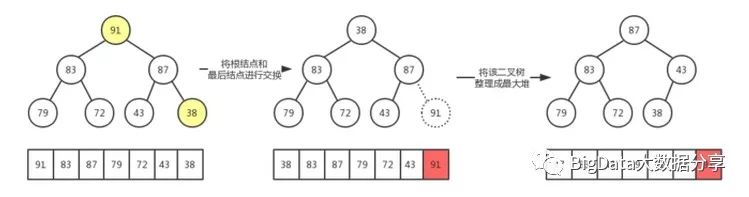
进过这一次排序之后,91 就处在最终的正确位置上,所以我们只需要对余下的最大堆进行操作!这里需要注意一点:
并不需要像创建最大堆时,从倒数第一个非叶子结点开始。因为在我们只是对第一个和最后一个结点进行了交换,所以只有根结点的顺序不满足最大堆的约束,我们只需要对第一个元素进行处理即可
2)、继续对结点87进行相同的操作:
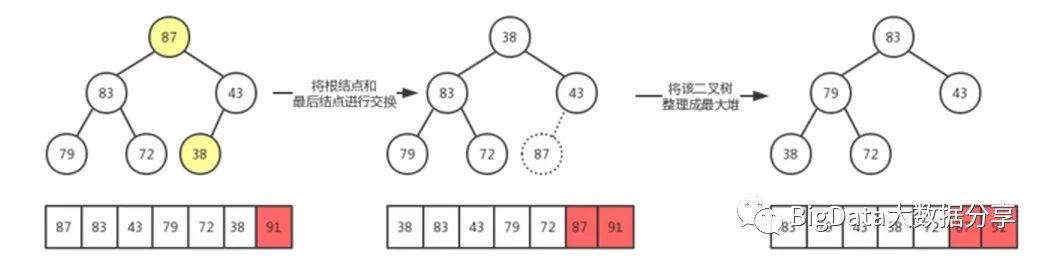
3)、现在我们来确定结点 83 的位置:
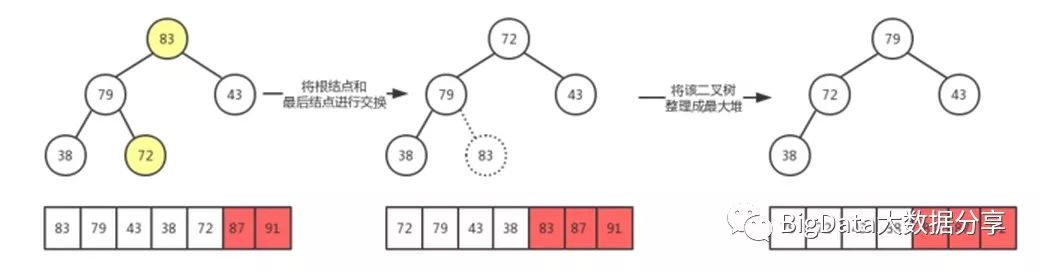
4)、经过上诉步骤就不难理解堆排序的原理所在,最后排序结果如下:
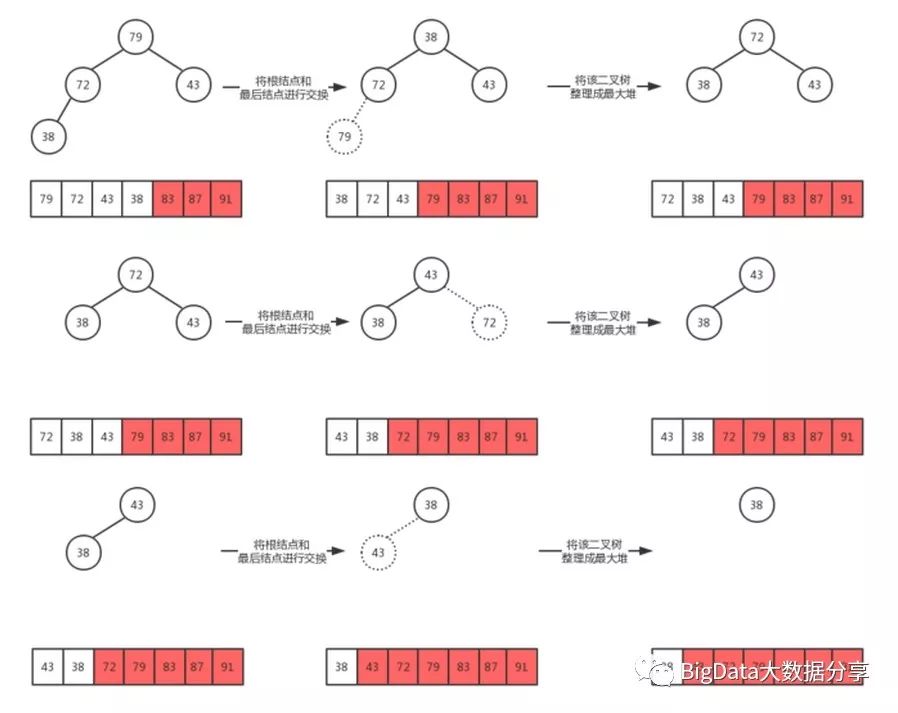
经过上诉多个步骤之后,最终的排序结果如下:
[38、43、72、79、83、87、91]
编码实现
这里需要对上面的代码进行一些修改!因为在排序中,我们的第0个元素是不用去放一个『哨兵』的,我们的元素从原来的第一个位置改为从第0个位置开始放置元素。
这样,数组之间的关系就发生了变化。那么对于任意一个下标为i(1 ≤ i ≤ n)的结点:
(1)、父结点为:(i - 1) / 2(i ≠ 0),若 i = 0,则 i 是根节点。
(2)、左子结点:2i - 1(2i - 1 ≤ n), 若不满足则无左子结点。
(3)、右子结点:2i (2i ≤ n),若不满足则无右子结点
堆排序和归并排序的时间时间复杂度是一样的O(N*LogN)。
总结
在分析完全二叉树的问题的时候,如果完全二叉树采用数组来顺序存储,需要牢记每一个结点和父结点之间的位置关系表示。具体参考上面的最大堆的介绍。

原创文章,欢迎转载,转载请注明原作者和出处。
据说帅哥靓女都关注了↓↓↓
喜欢请将下方小心心点亮
以上是关于最大堆(创建删除插入和堆排序)的主要内容,如果未能解决你的问题,请参考以下文章