堆的基本概念及堆排序

Posted 2021-05-01 取名无力症

Heapsort

Heap

上一篇文章，我们探讨了二叉树，其中我们引入了完全二叉树的概念，而二叉堆就可以看作一个近似的完全二叉树。
最大堆的递归定义为，子节点的值小于父节点的值，最大的元素位于堆顶
而最小堆的递归定义正好相反，子节点的值大于父节点的值，最小元素位于堆顶。
最大堆与最小堆的使用取决于具体场景，像最小堆一般用于构造优先队列。
In the previous article, we talked about the binary tree, in which we introduced the concept of a complete binary tree, and the binary heap can be seen as an approximate complete binary tree.
The recursion of the largest heap is defined as the value of the child node is less than the value of the parent node, and the largest element is at the top of the heap.
The recursive definition of the smallest heap is just the opposite. The value of the child node is greater than the value of the parent node, and the smallest element is at the top of the heap.
The use of the largest heap and the smallest heap depends on the specific scenario, like the smallest heap is generally used to construct the priority queue.

Maintaining the heap property

直接写代码吧!
show the code directly!
伪代码:
pseudocode:

PARENT(i)
    return int(i/2)
LEFT(i)
    return 2i
RIGHT(i)
    return 2i+1
MAX-HEAPIFY(A,i)
    l=left(i)
    r=right(i)
    if l<=A.heap-size and A[l]>A[i] #这里heapsize表示有多少个堆元素储存在堆中
        largest=l
    else largest=i
    if r<=A.heap-size and A[r]>A[largest]
        largest=r
    if largest!=i
        exchange A[i] with A[largst]
        MAX-HEAPIFY(A,largest)

python:

def parent(i):
    return int((i + 1) / 2) - 1
def left(i):
    return 2 * (i + 1) - 1
def right(i):
    return (i + 1) * 2
def MaxHeapify(A, i):
    l = left(i)
    r = right(i)
    if l < len(A) and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r < len(A) and A[r] > A[largest]:
        largest = r
    if largest != i:
        A[i], A[largest] = A[largest], A[i]
        MaxHeapify(A, largest)
A = [16,4,10,14,7,9,3,2,8,1]
MaxHeapify(A,1)

cpp:

#include<cstdio>
#include<algorithm>
int parent(int i)
{
    return ((i + 1) / 2) - 1;
}
int left(int i)
{
    return 2 * (i + 1) - 1;
}
int right(int i)
{
    return (i + 1) * 2;
}
void MaxHeapify(int *A,int i,int len)
{
    int l = left(i);
    int r = right(i);
    int largest;
    if(l<len&&A[l]>A[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }
    if(r<len&&A[r]>A[largest])
    {
        largest = r;
    }
    if(largest!=i)
    {
        std::swap(A[i], A[largest]);
        MaxHeapify(A, largest, len);
    }
}
int main(int argc, char const *argv[])
{
    int A[10] = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1};
    MaxHeapify(A, 1, 10);
    return 0;
}

接下来，我们用这个函数建堆
Now, we use this function to build a heap

Building a heap

我们这里直接看代码进行分析

#include<cstdio>
#include<algorithm>
int parent(int i)
{
    return ((i + 1) / 2) - 1;
}
int left(int i)
{
    return 2 * (i + 1) - 1;
}
int right(int i)
{
    return (i + 1) * 2;
}
void MaxHeapify(int *A,int i,int len)
{
    int l = left(i);
    int r = right(i);
    int largest;
    if(l<len&&A[l]>a[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }
    if(r<len&&A[r]>A[largest])
    {
        largest = r;
    }
    if(largest!=i)
    {
        std::swap(A[i], A[largest]);
        MaxHeapify(A, largest, len);
    }
}
void BuildHeap(int A[],int len)
{
    for (int i = len / 2 - 1; i >= 0; i--)
    {
        MaxHeapify(A, i, len);
    }
}
int main(int argc, char const *argv[])
{
    int A[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    BuildHeap(A, 10);
    return 0;
}

为什么要从A的中间开始并下降到0呢？
因为每次递减，i总是根，这样既减少了运算量，也使每次都能使MaxHeapify发挥作用，同理
Why start from the middle of A and drop to 0?
Because each time it is decreased, i is always the root, which reduces the amount of computation and makes MaxHeapify work every time.

def parent(i):
    return int((i + 1) / 2) - 1
def left(i):
    return 2 * (i + 1) - 1
def right(i):
    return (i + 1) * 2
def MaxHeapify(A, i):
    l = left(i)
    r = right(i)
    if l < len(A) and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r < len(A) and A[r] > A[largest]:
        largest = r
    if largest != i:
        A[i], A[largest] = A[largest], A[i]
        MaxHeapify(A, largest)
def BuildHeap(A):
    length = len(A)
    temp = int(length / 2)
    l=range(temp)
    for i in reversed(l):
        MaxHeapify(A,i)
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
BuildHeap(A)

至于时间复杂度，为啥确界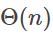是而不是

呢？

我看到过一个很有趣的做法，见于知乎链接

https://www.zhihu.com/question/264693363/answer/291397356

当然咯，如果按插入建堆就是的。

如果以上都能理解，那么接下来，堆排序就十分简单了。
As for time complexity，why the true bound is \(\Theta n\) rather than \(\Theta n\log n\)?
I saw an interesting way in知乎

https://www.zhihu.com/question/264693363/answer/291397356

of course, if you press Insert to build the heap is \(n\log n\).

The heapsort algorithm

def parent(i):
    return int((i + 1) / 2) - 1
def left(i):
    return 2 * (i + 1) - 1
def right(i):
    return (i + 1) * 2
def MaxHeapify(A, i,length):
    l = left(i)
    r = right(i)
    if l < length and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r < length and A[r] > A[largest]:
        largest = r
    if largest != i:
        A[i], A[largest] = A[largest], A[i]
        MaxHeapify(A, largest,length)
def BuildHeap(A,length):
    temp = int(length / 2)
    l=range(temp)
    for i in reversed(l):
        MaxHeapify(A, i,length)
def HeapSort(A):
    BuildHeap(A,len(A))
    length=len(A)
    for i in reversed(range(length)):
        A[0], A[i] = A[i], A[0]
        length = length - 1
        MaxHeapify(A, 0, length)
A = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
HeapSort(A)

#include<cstdio>
#include<algorithm>
int parent(int i)
{
    return ((i + 1) / 2) - 1;
}
int left(int i)
{
    return 2 * (i + 1) - 1;
}
int right(int i)
{
    return (i + 1) * 2;
}
void MaxHeapify(int *A,int i,int len)
{
    int l = left(i);
    int r = right(i);
    int largest;
    if(l<len&&A[l]>A[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }
    if(r<len&&A[r]>A[largest])
    {
        largest = r;
    }
    if(largest!=i)
    {
        std::swap(A[i], A[largest]);
        MaxHeapify(A, largest, len);
    }
}
void BuildHeap(int A[],int len)
{
    for (int i = len / 2 - 1; i >= 0; i--)
    {
        MaxHeapify(A, i, len);
    }

}
void HeapSort(int A[],int len)
{
    BuildHeap(A, 10);
    for (int i = len - 1;i>=0;i--)
    {
        std::swap(A[0], A[i]);
        len = len - 1;
        MaxHeapify(A, 0, len);
    }
}
int main(int argc, char const *argv[])
{
    int A[10] = {10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
    HeapSort(A, 10);
    return 0;
}

这里就是先构建一次二叉堆，堆顶元素为最大值，然后把他和最后一个元素调换，然后维护除最后一个元素的二叉堆，然后继续调换，……
Here is to build a binary heap first, the top element of the heap is the maximum value, then swap him and the last element, then maintain the binary heap except for the last element, and then continue to swap,……