左神直通BAT算法之堆排序
Posted 程序员弹药库
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了左神直通BAT算法之堆排序相关的知识,希望对你有一定的参考价值。
堆排序
什么是堆
堆结构就是将一颗完全二叉树映射到数组中的一种存储方式:
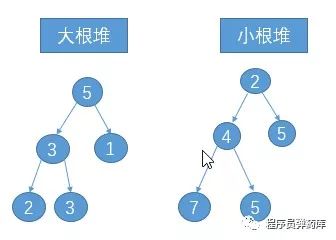
大根堆和小根堆
当堆的每一颗子树(包括树本身)的最大值就是其结点时称为大根堆;相反,当堆的每一颗子树的最小值就是其根结点时称为小根堆。其中大根堆的应用较为广泛,是一种很重要的数据结构。
heapInsert和heapify
大根堆最重要的两个操作就是 heapInsert和 heapify,前者是当一个元素加入到大根堆时应该自底向上与其父结点比较,若大于父结点则交换;后者是当堆中某个结点的数值发生变化时,应不断向下与其孩子结点中的最大值比较,若小于则交换。下面是对应的代码:
//index之前的序列符合大根堆排序,将index位置的元素加入堆结构,但不能破坏大根堆的特性
void heapInsert(int arr[],int index){
while (arr[index] > arr[(index - 1) / 2]) { //当该结点大于父结点时
swap(arr[index], arr[(index - 1) / 2]);
index = (index - 1) / 2; //继续向上比较
}
}
//数组中下标从0到heapSize符合大根堆排序
//index位置的值发生了变化,重新调整堆结构为大根堆
//heapSize指的是数组中符合大根堆排序的范围而不是数组长度,最大为数组长度,最小为0
void heapify(int arr[], int heapSize, int index){
int leftChild = index * 2 + 1;
while (leftChild < heapSize) { //当该结点有左孩子时
int greatOne = leftChild + 1 < heapSize && arr[leftChild + 1] > arr[leftChild] ?
leftChild + 1 : leftChild; //只有当右孩子存在且大于左孩子时,最大值是右孩子,否则是左孩子
greatOne = arr[greatOne] > arr[index] ? greatOne : index;//将父结点与最大孩子结点比较,确定最大值
if (greatOne == index) {
//如果最大值是本身,则不用继续向下比较
break;
}
swap(arr[index], arr[greatOne]);
//next turn下一轮
index = greatOne;
leftChild = index * 2 + 1;
}
}
建立大根堆
void buildBigRootHeap(int arr[],int length){
if (arr == NULL || length <= 1) {
return;
}
for (int i = 0; i < length; ++i) {
heapInsert(arr, i);
}
}
利用heapify排序
前面做了那么多铺垫都是为了建立大根堆,那么如何利用它来排序呢?
对应代码实现如下:
void heapSort(int arr[],int length){
if (arr == NULL || length <= 1) {
return;
}
//先建立大根堆
for (int i = 0; i < length; ++i) {
heapInsert(arr, i);
}
//循环弹出堆顶元素并heapify
int heapSize = length;
swap(arr[0], arr[--heapSize]);//相当于弹出堆顶元素
while (heapSize > 0) {
heapify(arr, heapSize, 0);
swap(arr[0], arr[--heapSize]);
}
}
int main(){
int arr[] = {9,7,1,3,6,8,4,2,5};
heapSort(arr, 9);
travles(arr, 9);
return 0;
}
堆排序的优势在于无论是入堆一个元素 heapInsert还是出堆一个元素之后的 heapify都不是将整个样本遍历一遍( O(n)级别的操作),而是树层次上的遍历( O(logn)级别的操作)。
这样的话堆排序过程中,建立堆的时间复杂度为 O(nlogn),循环弹出堆顶元素并 heapify的时间复杂度为 O(nlogn),整个堆排序的时间复杂度为 O(nlogn),额外空间复杂度为 O(1)
出自:http://www.zhenganwen.top
已获授权
作者是前腾讯员工/现创业公司员工,致力于分享leetcode/剑指offer/算法题解/互联网时事/编程资源,觉得不错关注转发一下。
以上是关于左神直通BAT算法之堆排序的主要内容,如果未能解决你的问题,请参考以下文章