排序算法堆排序

Posted 2021-05-01 程序员思语

无论从事编程的哪一个方向，负责哪块业务或者从事某块岗位，都离不开算法的历练，接触岗位、业务越多，越觉得语言只是工具，而算法和编程解决思路才是根本。
友情提示：阅读本文大概需要 30分钟

前言

堆是一种特殊的树形数据结构，即完全二叉树。堆分为大根堆和小根堆，大根堆为根节点的值大于两个子节点的值；小根堆为根节点的值小于两个子节点的值，同时根节点的两个子树也分别是一个堆。

二叉堆

二叉堆本质上是一种完全二叉树，它分为：最大堆、最小堆。什么是最大堆呢？最大堆任何一个父节点的值，都大于等于它左右孩子节点的值；相对的，最小堆任何一个父节点的值，都小于等于它左右孩子节点的值。

二叉堆的根节点叫做堆顶。最大堆和最小堆的特点，决定了在最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

---

堆的自我调整

对于二叉堆，如下有几种操作：插入节点、删除节点、构建二叉堆。这几种操作都是基于堆的自我调整。下面让我们以最小堆为例，看一看二叉堆是如何进行自我调整的。

1.插入节点

二叉堆的节点插入，插入位置是完全二叉树的最后一个位置。比如

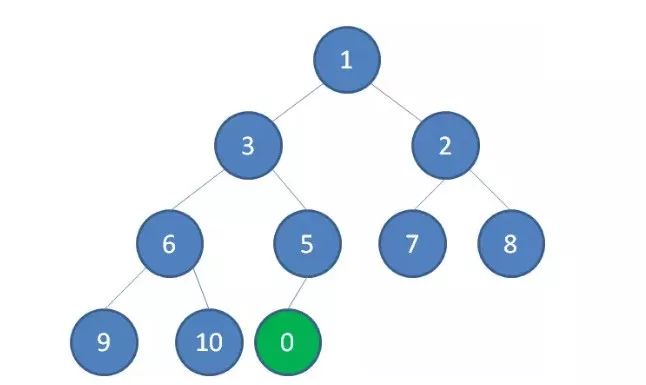
• 1.我们插入一个新节点，值是 0。

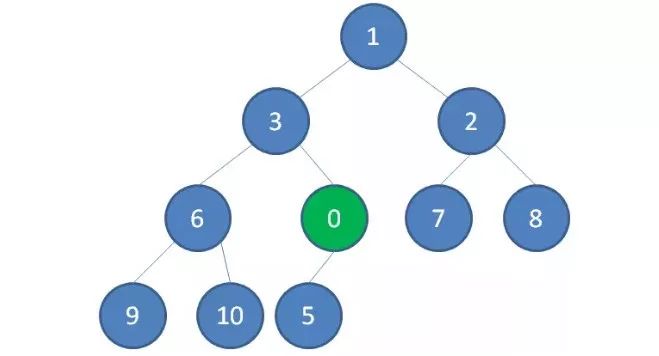
• 2.我们让节点0的它的父节点5做比较，如果0小于5，则让新节点“上浮”，和父节点交换位置。

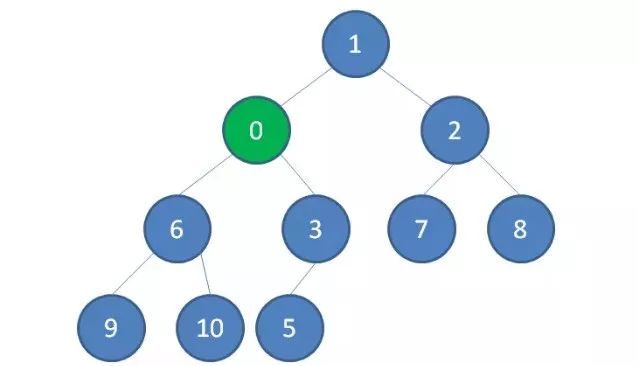
• 3.继续用节点0和父节点3做比较，如果0小于3，则让新节点继续“上浮”。

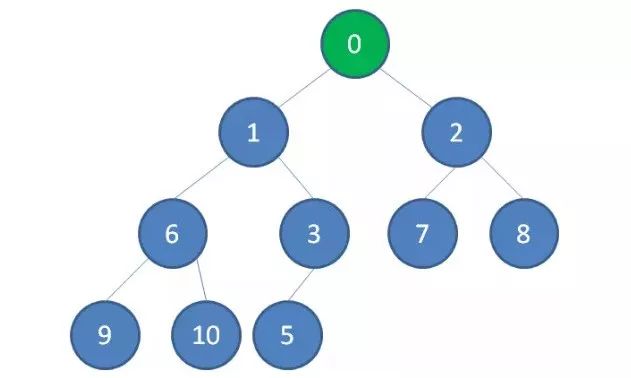
• 4.继续比较，最终让新节点0上浮到了堆顶位置。

  ---

  
  

  
  

2.删除节点

二叉堆的节点删除过程和插入过程正好相反，所删除的是处于堆顶的节点。比如

• 1.我们删除最小堆的堆顶节点1。

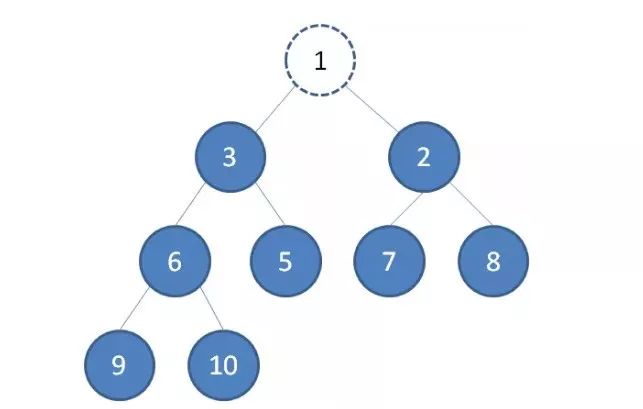
• 2.为了维持完全二叉树的结构，我们把堆的最后一个节点10补到原本堆顶的位置。

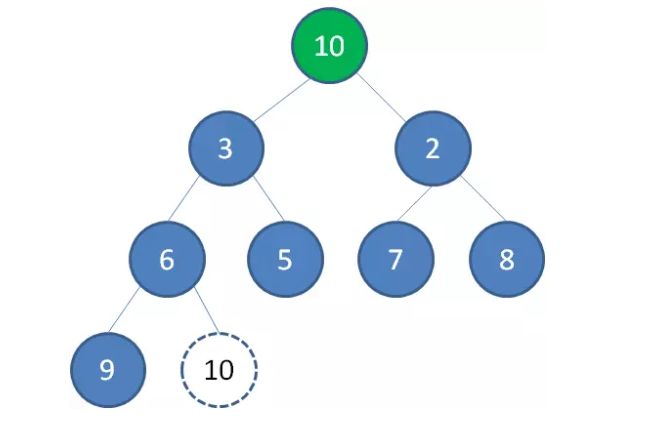
• 3.接下来我们让移动到堆顶的节点10和它的左右孩子进行比较，如果左右孩子中最小的一个（显然是节点2）比节点10小，那么让节点10“下沉”。

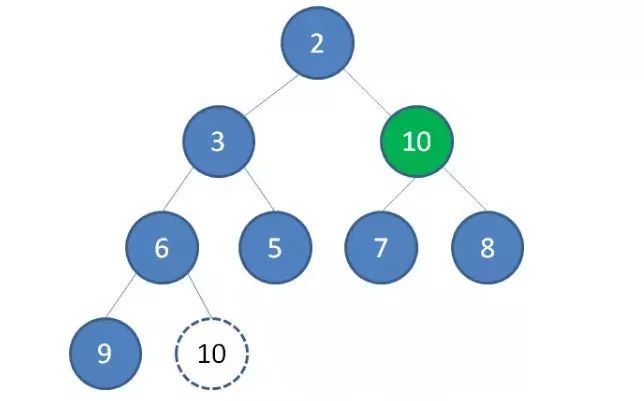
• 4.继续让节点10和它的左右孩子做比较，左右孩子中最小的是节点7，由于10大于7，让节点10继续“下沉”。

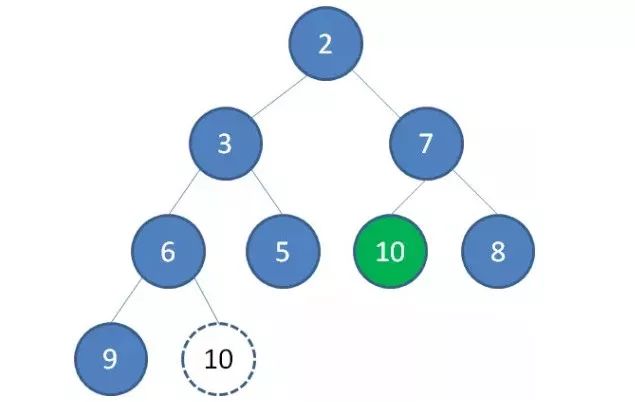
这样一来，二叉堆重新得到了调整。

---

3.构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让所有非叶子节点依次下沉。

我们举一个无序完全二叉树的例子：

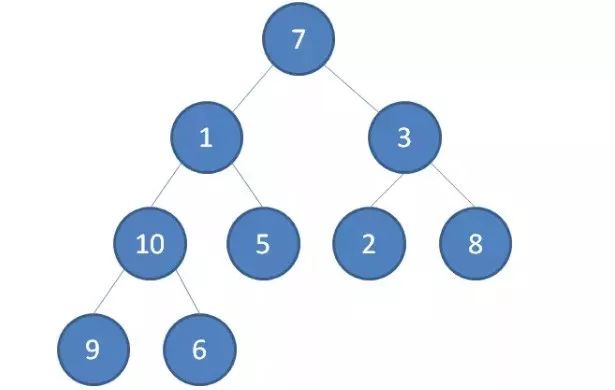
• 1.首先，我们从最后一个非叶子节点开始，也就是从节点10开始。如果节点10大于它左右孩子中最小的一个，则节点10下沉。

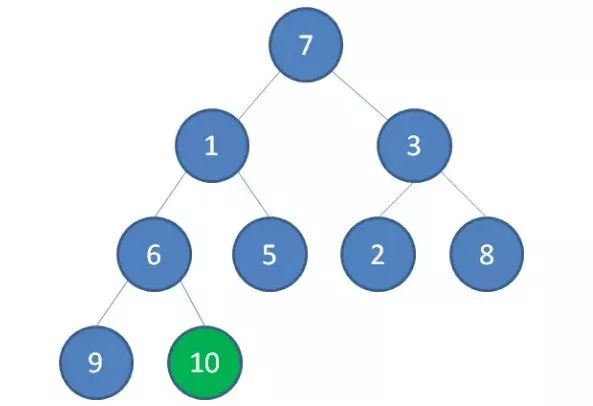
• 2.接下来轮到节点3，如果节点3大于它左右孩子中最小的一个，则节点3下沉。

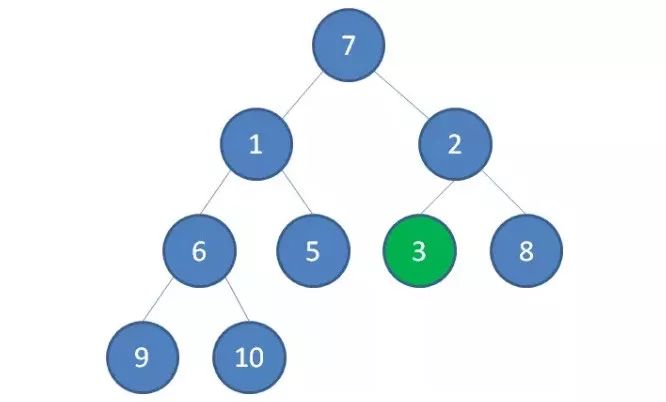
• 3.接下来轮到节点1，如果节点1大于它左右孩子中最小的一个，则节点1下沉。事实上节点1小于它的左右孩子，所以不用改变。接下来轮到节点7，如果节点7大于它左右孩子中最小的一个，则节点7下沉。

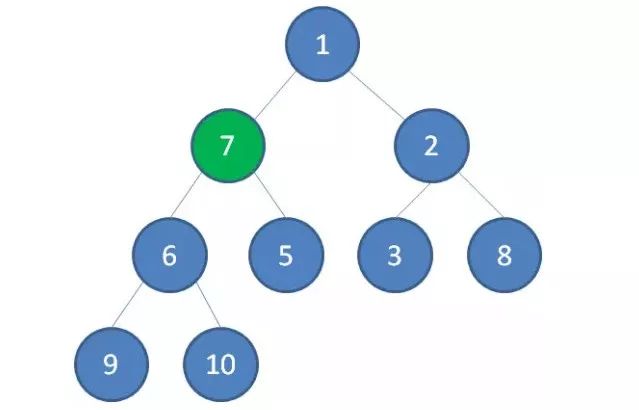
• 4.节点7继续比较，继续下沉。

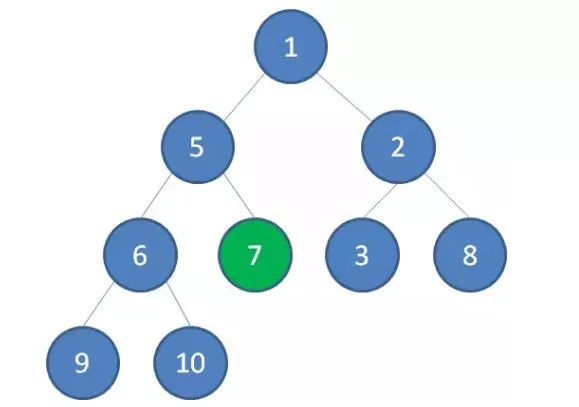
这样一来，一颗无序的完全二叉树就构建成了一个最小堆。

---

注意

二叉堆虽然是一颗完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组当中。
数组中，在没有左右指针的情况下，如果要定位到一个父节点的左孩子和右孩子，可以通过数组下标来计算。假设父节点的下标是parent，则它的左孩子下标就是 2parent+1, 它的右孩子下标就是 2parent+2 。

堆排序

二叉堆和最大堆的特性：①.二叉堆本质上是一种完全二叉树;②.最大堆的堆顶是整个堆中的最大元素。当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

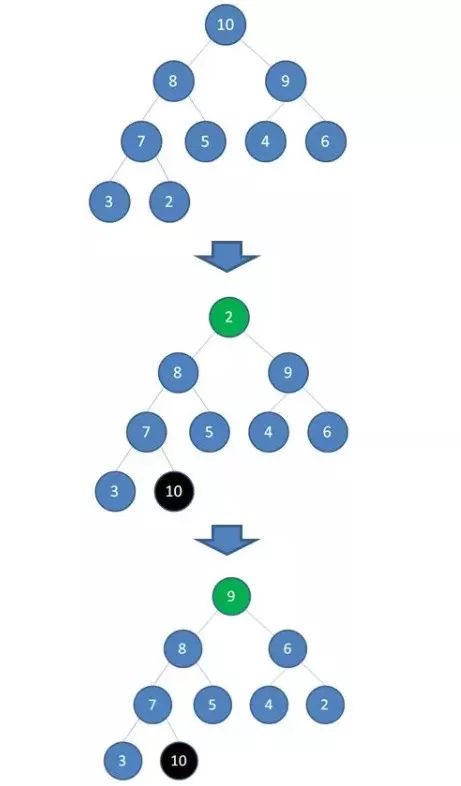
正如上图所示，当我们删除值为10的堆顶节点，经过调节，值为9的新节点就会顶替上来；当我们删除值为9的堆顶节点，经过调节，值为8的新节点就会顶替上来…….

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

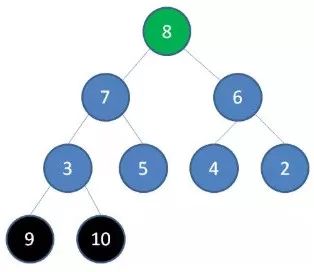
• 1.删除节点9，节点8成为新堆顶：

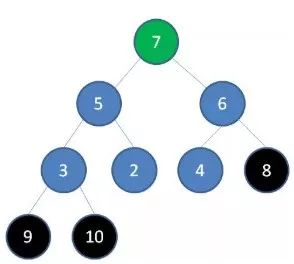
• 2.删除节点8，节点7成为新堆顶：

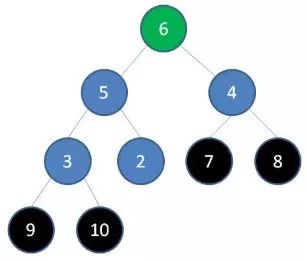
• 3.删除节点7，节点6成为新堆顶：

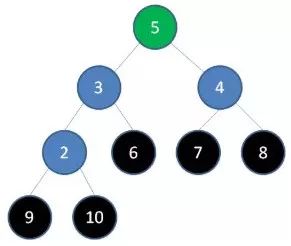
• 4.删除节点6，节点5成为新堆顶：

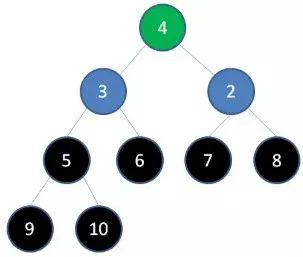
• 5.删除节点5，节点4成为新堆顶：

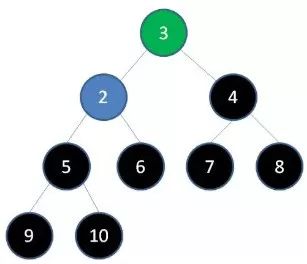
• 6.删除节点4，节点3成为新堆顶：

• 7.删除节点3，节点2成为新堆顶：

到此为止，我们原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

由此，我们可以归纳出堆排序算法的步骤：

• 1. 把无序数组构建成二叉堆。

• 2. 循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

// C++
#include<iostream>
#include<vector>
using namespace std;

// 递归方式构建大根堆(len是arr的长度，index是第一个非叶子节点的下标)
void adjust(vector<int> &arr, int len, int index) {
    int left = 2*index + 1; // index的左子节点
    int right = 2*index + 2;// index的右子节点

    int maxIdx = index;
    if(left<len && arr[left] > arr[maxIdx])     maxIdx = left;
    if(right<len && arr[right] > arr[maxIdx])     maxIdx = right;

    if(maxIdx != index)
    {
        swap(arr[maxIdx], arr[index]);
        adjust(arr, len, maxIdx);
    }

}

// 堆排序
void heapSort(vector<int> &arr, int size) {
    // 构建大根堆（从最后一个非叶子节点向上）
    for(int i=size/2 - 1; i >= 0; i--)
    {
        adjust(arr, size, i);
    }

    // 调整大根堆
    for(int i = size - 1; i >= 1; i--)
    {
        swap(arr[0], arr[i]);           // 将当前最大的放置到数组末尾
        adjust(arr, i, 0);              // 将未完成排序的部分继续进行堆排序
    }
}

int main() {
    vector<int> arr = {8, 1, 14, 3, 21, 5, 7, 10};
    heapSort(arr, arr.size());
    for(int i=0;i<arr.size();i++)
    {
        cout<<arr[i]<<endl;
    }
    return 0;
}

二叉堆的节点下沉调整（downAdjust 方法）是堆排序算法的基础，这个调节操作本身的时间复杂度是多少呢？假设二叉堆总共有n个元素，那么下沉调整的最坏时间复杂度就等同于二叉堆的高度，也就是O（logn）。我们再来回顾一下堆排序算法的步骤：

第一步，把无序数组构建成二叉堆，需要进行n/2次循环。每次循环调用一次 downAdjust 方法，所以第一步的计算规模是  n/2 * logn，时间复杂度 O（nlogn）。

第二步，需要进行n-1次循环。每次循环调用一次 downAdjust 方法，所以第二步的计算规模是 （n-1） * logn ，时间复杂度 O（nlogn）。

两个步骤是并列关系，所以整体的时间复杂度同样是 O（nlogn）。

总结

与堆排序和快速排序相比

相同：堆排序和快速排序的平均时间复杂度都是O(nlogn)，并且都是 不稳定排序。

不同：快速排序的最坏时间复杂度是O(n^2)，而堆排序最坏时间复杂度稳定在O(nlogn)；快速排序的递归和非递归方法空间复杂度都是O(n)，而堆排序的空间复杂度是O(1)。

最后

今天的 排序算法（六）堆排序 就分享到这里，有问题欢迎大家留言，谢谢 ~