GCTT 出品 | 阅读挑战:Go 的堆排序
Posted Go语言中文网
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GCTT 出品 | 阅读挑战:Go 的堆排序相关的知识,希望对你有一定的参考价值。

image
堆排序是一种漂亮的排序算法。它使用一个最大堆对一系列数字或其他定义了顺序关系的元素进行排序。在这篇文章里,我们将深入探究 Go 标准库中堆排序的实现。
最大堆
First a short recap on binary max-heaps. A max-heap is a container that provides its maximum element in O(1) time, adds an element in O(log n), and removes the maximum element in O(log n).
首先来简单重述一下 最大二叉堆。最大堆是一个容器,能在 O(1) 时间内取出最大元素,在 O(log n) 的时间内增加一个元素,删除最大元素也是 O(log n) 时间。
最大堆是近似满二叉树,它的每个节点都大于或等于其子节点。在这篇文章中,我将后者称之为堆特性。
这两个特性一起定义出一个最大堆:
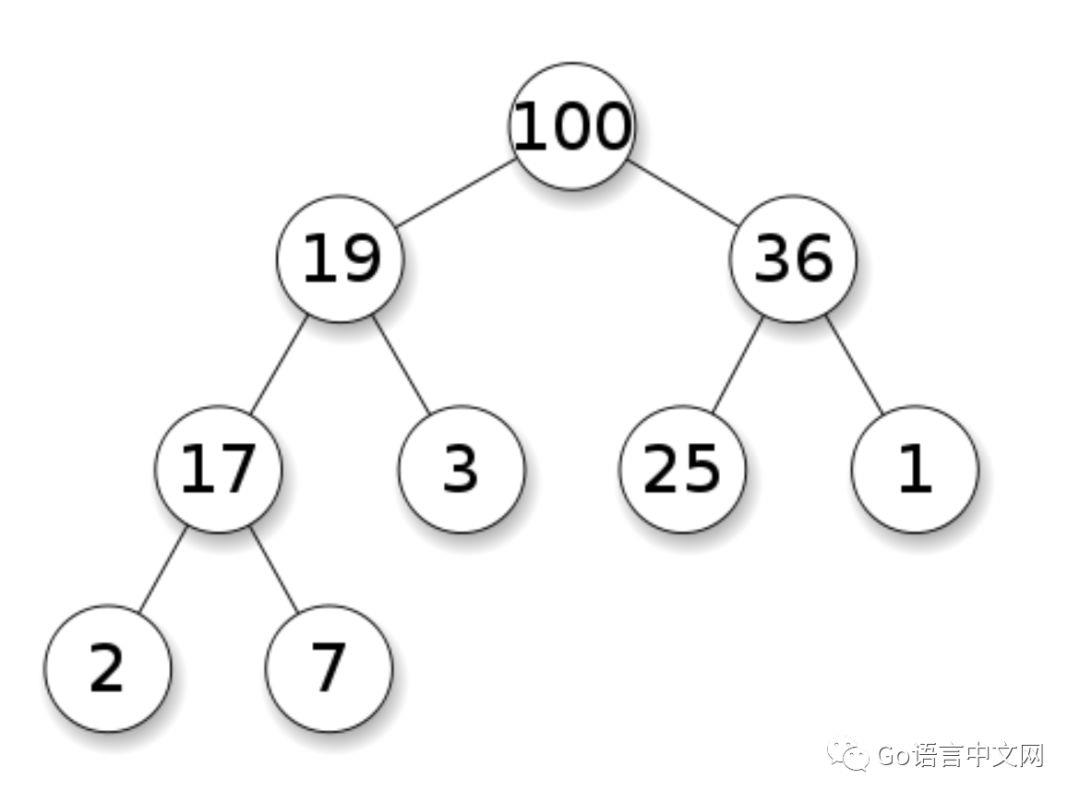
在堆的算法里,最大堆用一个数组来表示。在数组表示中,第 i 个元素的子节点位于 2*i+1 和 2*i+2。下面这个来自维基百科的图解释了数组表示:

构建一个堆
一个数组可以在 O(n) 时间内转换成一个最大堆。很神奇,是不是?算法如下:
将输入数组看作一个堆。它尚未满足堆特性。
从倒数第二层开始对堆上的节点进行遍历 —— 即叶节点上面的一层 —— 直到根节点。
对每个节点,将它向下传送,直到它已经比它的两个子节点都大。向下传送时,总是与较大的子节点进行交换。
就是这样,你做到了!
为什么可行?我将试图用这个大手一挥的证据让你信服(如果想跳过,请随意):
考虑树的一个节点
x。因为我们从后往前遍历堆,当我们到达节点x时,它两边的子树都已经满足了堆特性。如果
x比它的两个子节点都要大,那我们就搞定了。否则,我们将
x与它最大的子节点进行交换。这就让新的根节点就比它的两个子节点都大。如果
x在新的子树上不满足堆特性,上述过程就会一直重复,直到满足或直到它变成叶节点,即它不再有子节点。
这对堆上的每个节点都是成立的,包括根节点。
堆排序算法
现在开始正课 —— 堆排序。
堆排序的工作过程分两个步骤:
使用上面展示的算法,从输入数组构建一个最大堆。这需要 O(n) 的时间。
从堆中弹出元素放到输出数组中,从后往前填充。每次从堆中弹出元素需要 O(log n) 时间,整个容器加起来为 O(n * log n)。
Go 实现的一个很酷的特性,是它使用输入数组来存放输出,因此避免了为输出分配 O(n) 的内存。
堆排序的实现
Go 的排序库支持任何 索引为整数,元素之间有 定义好的顺序关系,并且支持在两个索引之间交换元素的集合。
1type Interface interface {
2 // Len is the number of elements in the collection.
3 Len() int
4 // Less reports whether the element with
5 // index i should sort before the element with index j.
6 Less(i, j int) bool
7 // Swap swaps the elements with indexes i and j.
8 Swap(i, j int)
9}
自然地,任何数字组成的连续容器都可以满足这个接口。
现在让我们来看一下 heapSort 的函数体。
1func heapSort(data Interface, a, b int) {
2 first := a
3 lo := 0
4 hi := b - a
5
6 // Build heap with greatest element at top.
7 for i := (hi - 1) / 2; i >= 0; i-- {
8 siftDown(data, i, hi, first)
9 }
10
11 // Pop elements, largest first, into end of data.
12 for i := hi - 1; i >= 0; i-- {
13 data.Swap(first, first+i)
14 siftDown(data, lo, i, first)
15 }
16}
函数的签名有点晦涩,不过看了前三行就清楚了:
a和b是data中的索引。heapSort(data, a, b)对 data 的半开区间[a, b)进行排序。first是a的一个拷贝。lo和hi是由a-lo标准化的索引,永远从零开始,而hi与输入数组的长度一致。
接下来的代码构建最大堆:
1// Build heap with greatest element at top.
2for i := (hi - 1) / 2; i >= 0; i-- {
3 siftDown(data, i, hi, first)
4}
如我们先前所见,这段代码从叶节点的上一层扫描堆并调用 shiftDown() 将当前元素往下传送直至它满足堆特性。下面我将深入 shiftDown() 的更多细节。
在这一步,data 是一个最大堆。
接下来,我们弹出所有元素来创建一个有序的数组。
1// Pop elements, largest first, into end of data.
2for i := hi - 1; i >= 0; i-- {
3 data.Swap(first, first+i)
4 siftDown(data, lo, i, first)
5}
在这个循环里,i 是堆的最后一个索引。在每个迭代中:
堆的最大元素
first与堆的最后一个元素进行交换。通过将新的
first元素向下传送直至它满足堆特性来恢复堆特性。堆的大小
i减一。
换句话说,我们从后往前填充数组,从最大的元素开始,直到倒数第二小的元素。结果就是将输入数组进行了排序。
维持堆特性
在整篇文章中,我使用 shitDown() 来维持堆特性。让我们来看看它是如何工作的:
1// siftDown implements the heap property on data[lo, hi).
2// first is an offset into the array where the root of the heap lies.
3func siftDown(data Interface, lo, hi, first int) {
4 root := lo
5 for {
6 child := 2*root + 1
7 if child >= hi {
8 break
9 }
10 if child+1 < hi && data.Less(first+child, first+child+1) {
11 child++
12 }
13 if !data.Less(first+root, first+child) {
14 return
15 }
16 data.Swap(first+root, first+child)
17 root = child
18 }
19}
这段程序将 root 位置的元素一直向下传送直到它比它的两个子节点都大。当往下走一级时,这个元素将和它较大的子节点进行交换。这是为了保证新的父节点比它两个子节点都大。
3 与其最大的子节点
10 进行交换
前面的几行计算第一个子节点的索引并确认它存在:
1child := 2*root + 1
2if child >= hi {
3 break
4}
child >= hi 意味着当前的 root 是叶节点,所以算法结束。
接下来,我们选两个子节点中较大的一个。
1if child+1 < hi && data.Less(first+child, first+child+1) {
2 child++
3}
因为任意节点的子节点在数组中都是相邻的,所以 child++ 选择了第二个子节点。
然后,我们检查一下父节点是否确实比子节点小:
1if !data.Less(first+root, first+child) {
2 return
3}
如果父节点比它的最大子节点要大,我们就搞定,所以返回。
最后,如果父节点小于子节点我们就将二者交换并将 root 的值更新准备下一轮迭代。
1data.Swap(first+root, first+child)
2root = child
结论
这是第三篇针对我读到的不熟悉的代码片段进行解释而写的文章。我喜欢这样的体验,因为它教会我如何读代码并就此进行交流。请在下面留下你的评论和反馈。
via: https://blog.bitsrc.io/reading-challenge-heap-sort-in-go-93115239accd
本文由 GCTT 原创编译,Go 中文网 荣誉推出
以上是关于GCTT 出品 | 阅读挑战:Go 的堆排序的主要内容,如果未能解决你的问题,请参考以下文章