算法那些事儿之堆排序
Posted Orange技术那些事儿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法那些事儿之堆排序相关的知识,希望对你有一定的参考价值。
算法和数据结构可能是大多数初级程序员都不喜欢了解的知识,毕竟涉及到很多数学算法,之前曾经看过一些老师讲解的课程,讲解了程序员应该了解的数学知识,如果仔细了解的话,应该会发现,无论什么编程语言都包含了数学概念,而且,越深入学习越需要了解更多的算法和数据结构知识
前言
堆排序作为排序算法里的一种,本身而言不算特别复杂,需要认真理解即可明白,写这篇主要是因为源码学习中涉及到了,而且本身也需要在学习算法和数据结构时做一个总结,故在这里说明堆排序的相关知识
定义
参考维基百科的解释:
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
若以升序排序说明,把阵列转换成最大堆积(Max-Heap Heap),这是一种满足最大堆积性质(Max-Heap Property)的二元树:对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。重复从最大堆积取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆积维持最大堆积性质。
堆排序一定要明白‘堆’这种数据结构的特点,不要死记,理解堆这种数据结构是最重要的
说明
若以升序排列,我们需要使用最大堆来找出其中最大的那个值,因为最大堆性质表明父节点需要大于等于子节点,那么二叉树的根节点一定是这个堆中最大的值,然后将最大值与最后一个节点交换,这样最后一个节点即为最大值。之后最后一个代表的最大值的节点不参与最大堆的排序过程,剩余节点重复这个过程即可得到一个升序的数列
降序排列则需要使用最小堆来找出其中最小的那个值,其他过程同上
通常情况,堆是通过一维数组实现的,以升序排列为例整个实现流程如下:
将排序的数组中所有数按二叉树形式对号入座
从最后一个非叶子节点开始,子节点存在则比较其和其子节点的值的大小,如果其小于子节点中的最大值,则交换节点,其将更新为这个子树中最大值的节点
如果父节点和子节点进行了交换,有可能破坏了子节点堆的特性,则为了满足堆的特性,需要处理子节点使其满足条件,递归执行2直到所有子节点都满足条件
重复第2,3步,循环向前遍历直到根节点
将根节点,即堆顶(现在为数组中第一个值)与最后一个值交换
数组长度减1(排除最后一个已经算出的最大值),重复1-5,直到排序的数组长度为1,则表明排序完成
第一步就是以数组形式表示二叉树,不做任何代码操作,把需要排序的数组部分想象成二叉树
整体上主要分为2部分,一部分在于数组的最大堆化,另一部分在于数组节点交换
举例说明
这里举例说明,执行的过程,比如数组[32, 4, 14, 56, 33, 78],排序过程如下
第一步,将数组以二叉树排列
第二步,找到最后一个非叶子节点14,比较其和其子节点的大小,14小于78,则将78和14交换,继续看交换后节点14位置,没子节点,不用向下验证
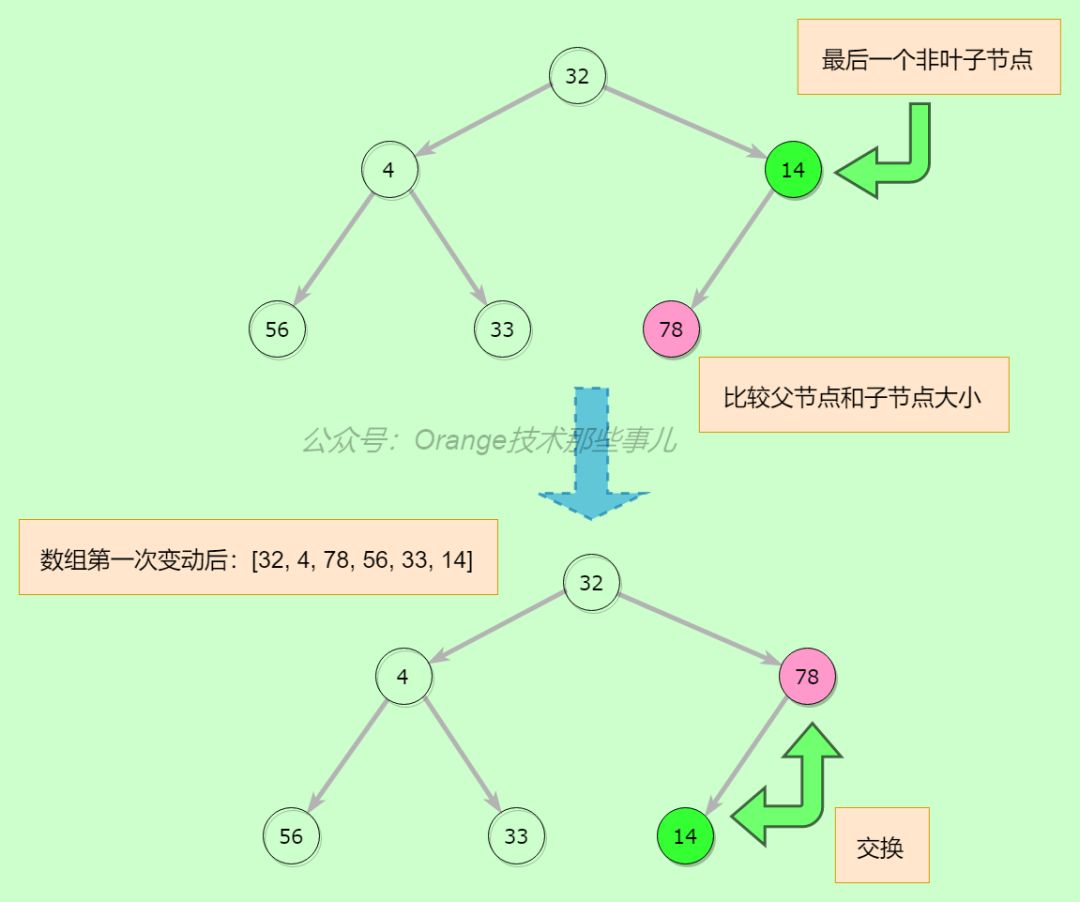
第三步,继续前一个节点4的比较,子节点56最大,交换56和4,继续看交换后节点4的位置,没子节点,不用向下验证
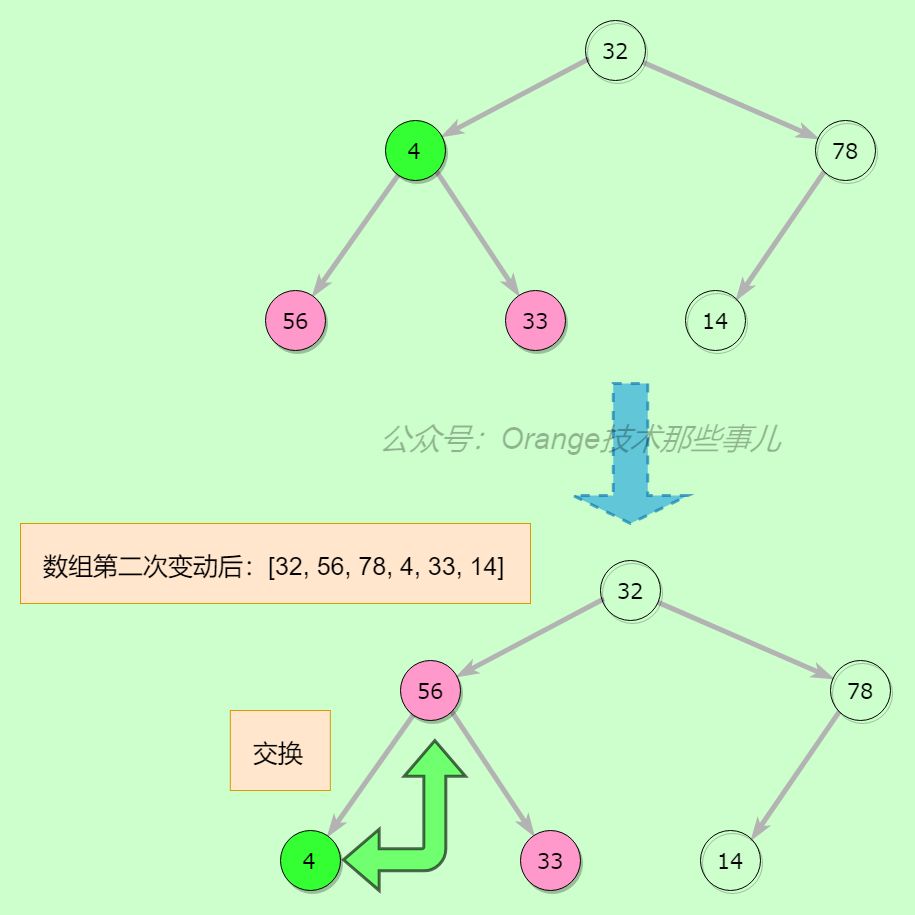
第四步,继续前一个节点32的比较,子节点78最大,交换32和78,继续看交换后32的位置,验证,32大于14,不用交换
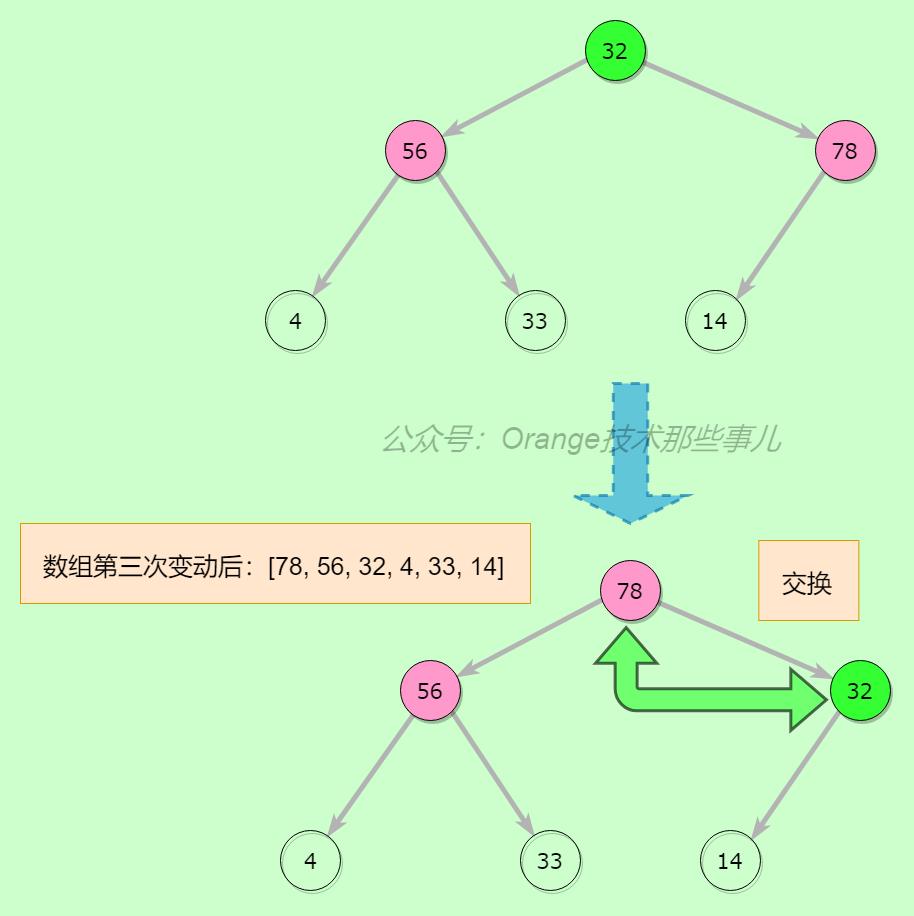
执行完上一步之后,我们可以看出整个堆是平衡的了,数组不是有序的,所以要明白的,我们用最大堆找到的是堆顶,堆顶是这个堆中最大的值,即根节点,数组索引为0的元素,下面要做的就是不断循环这个过程
将堆顶元素78与数组最后一个值交换位置,此时堆顶元素变为14,堆容量减1,我们需要重新平衡整个堆(最后的78不再参与堆平衡)
第五步,继续从最后一个非叶子节点开始平衡,56节点已经平衡,14与56交换,继续看交换后14的位置,33大于14,交换33和14,继续看交换后节点14的位置,无子节点,不用继续向下验证
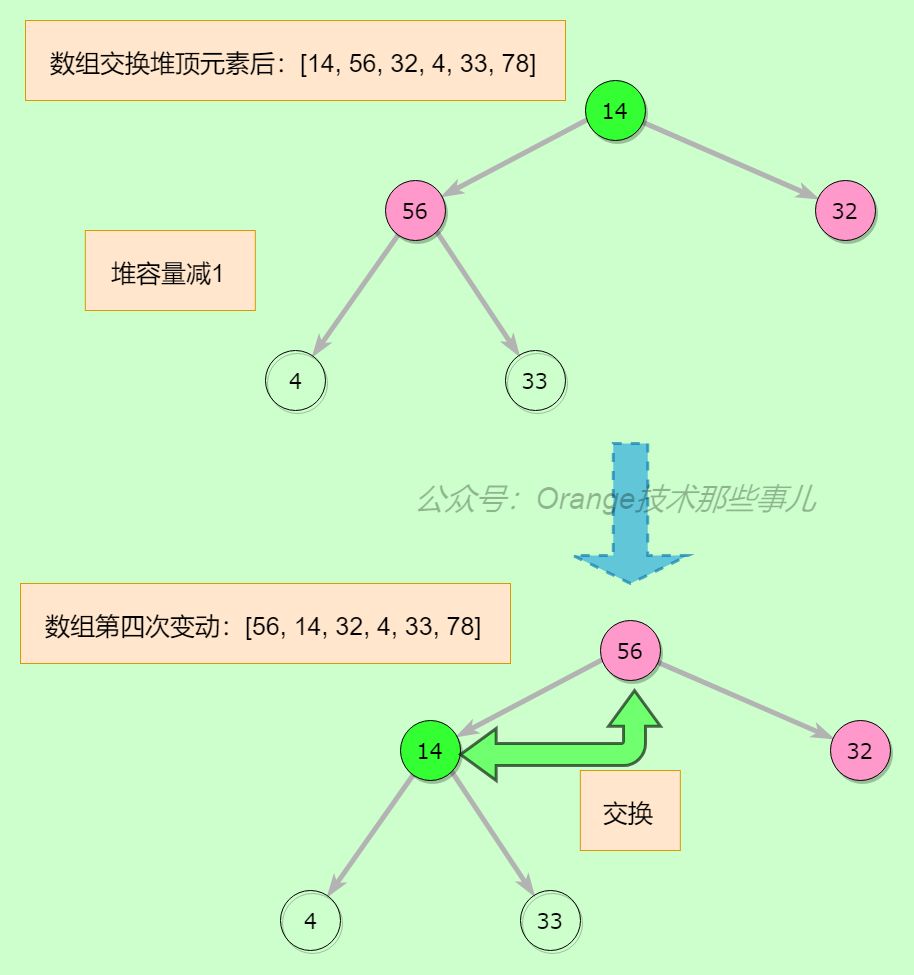
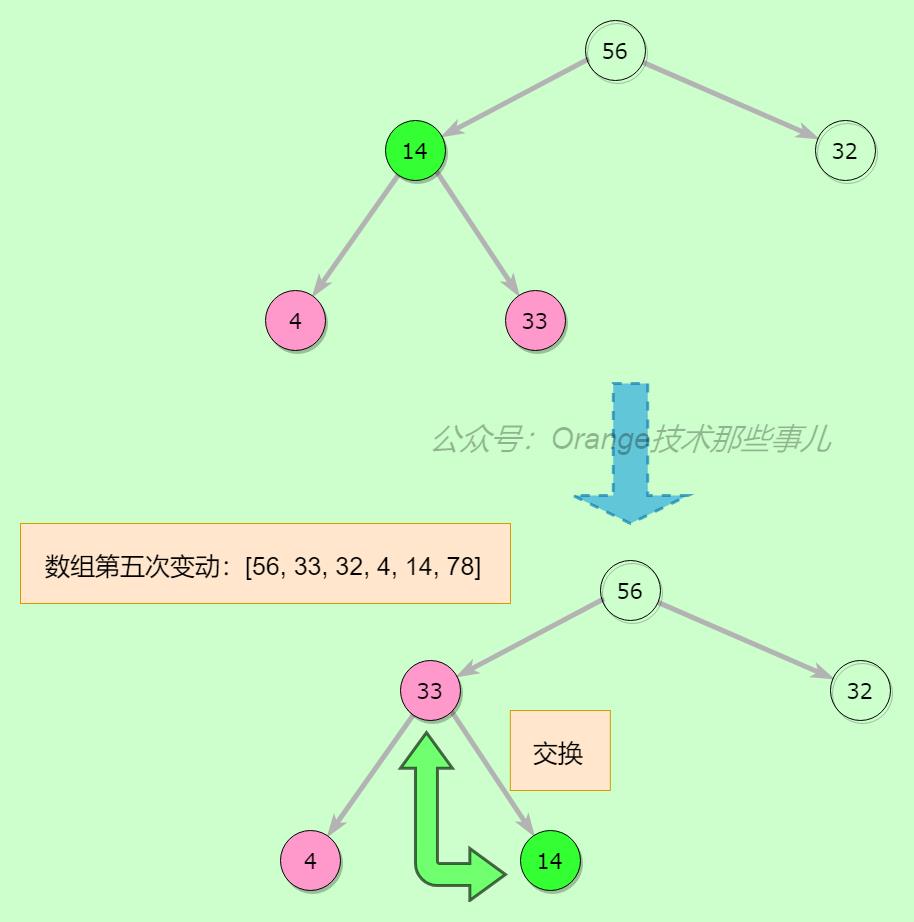
上一步执行完,整个堆又平衡了,堆顶元素交换,堆容量减1再继续平衡
第六步,继续从最后一个非叶子节点开始平衡,33节点已经平衡,14与33交换,继续看交换后14的位置,14已经平衡,不用交换操作了
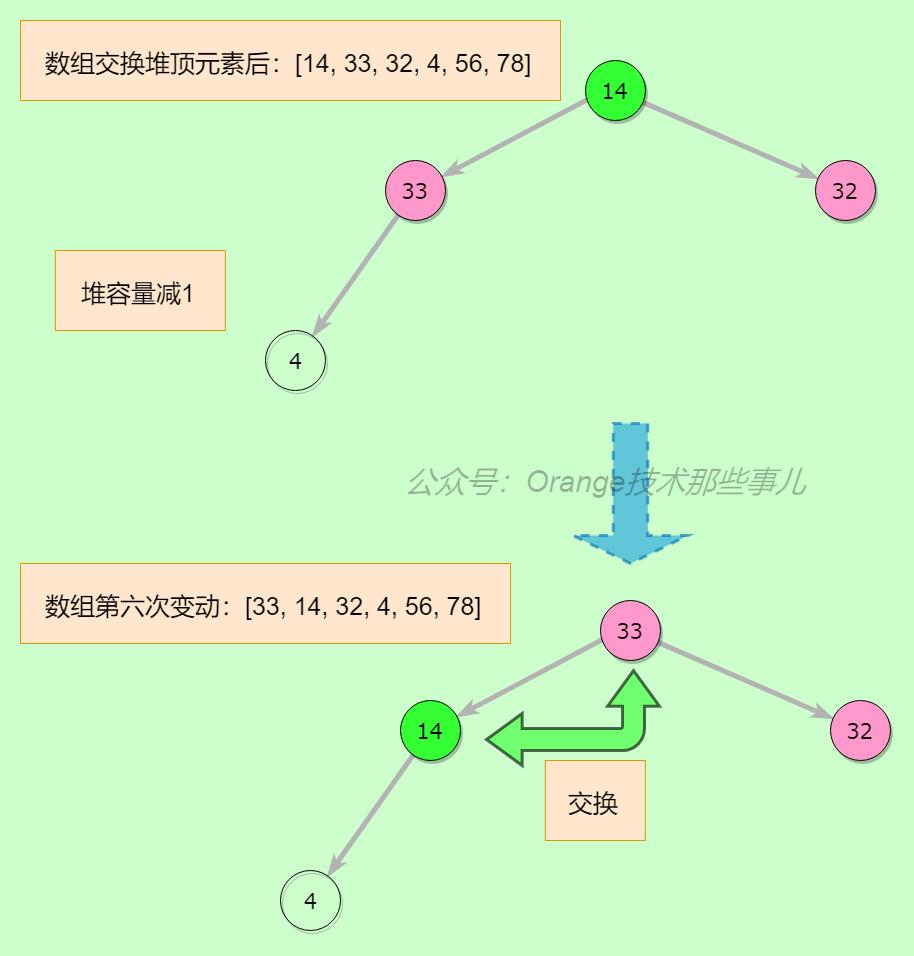
上一步执行完,整个堆又平衡了,堆顶元素交换,堆容量减1再继续平衡
第七步,继续从最后一个非叶子节点开始平衡,4与32交换,继续看交换后4的位置,无子节点,不用交换操作了
上一步执行完,整个堆又平衡了,堆顶元素交换,堆容量减1再继续平衡
第八步,继续从最后一个非叶子节点开始平衡,此时只剩下两个节点4和14,但是不满足堆的特性,我们还要继续,14和4交换,平衡,堆顶元素交换,排序完成
代码实现
public class HeapSort {
/**
* 数组变动次数,只是为了记录
*/
private static int time = 0;
public static void sort(int[] arrays) {
// 记录需要排序的数组长度,已经交换排好的部分需要排除
int heapLength = arrays.length;
// 循环堆化和交换的过程
while (heapLength > 1) {
// 1.将数组最大堆化
maxHeapify(arrays, heapLength);
System.out.println("数组堆化后:"+Arrays.toString(arrays));
// 2.交换堆顶元素和最后一个元素,这样就排好了最后一个元素
swap(arrays, heapLength);
System.out.println("数组交换堆顶元素后:"+Arrays.toString(arrays));
// 每次heapLength需减1
heapLength--;
}
}
private static void maxHeapify(int[] arrays, int heapLength) {
// 从最后一个非叶子节点开始,最后一个非叶子节点 为 (heapLength >>> 1) - 1
for (int i = (heapLength >>> 1) - 1; i >= 0; i--) {
// 保存当前索引位置
int currentIndex = i;
// (currentIndex << 1) + 1 为当前节点左子节点索引
// (currentIndex << 1) + 2 为当前节点右子节点索引
int leftChildIndex = (currentIndex << 1) + 1;
int rightChildIndex = leftChildIndex + 1;
// 子节点中最大值的索引
int maxChildIndex = -1;
// 判断当前节点是否有子节点
while (leftChildIndex <= (heapLength - 1)) {
// 先赋值
maxChildIndex = leftChildIndex;
// 右子节点存在,则找子节点中的最大值
if (rightChildIndex <= (heapLength - 1) && arrays[leftChildIndex] < arrays[rightChildIndex]) {
maxChildIndex = rightChildIndex;
}
if (arrays[maxChildIndex] > arrays[currentIndex]) {
// 和子节点交换当前索引值
int temp = arrays[currentIndex];
arrays[currentIndex] = arrays[maxChildIndex];
arrays[maxChildIndex] = temp;
time++;
System.out.println("数组第" + time + "次变动" + Arrays.toString(arrays));
}
// 继续判断交换后原子节点处是否满足堆的特性,直到当前节点下的局部二叉树完全满足堆的特性
leftChildIndex = (maxChildIndex << 1) + 1;
rightChildIndex = leftChildIndex + 1;
currentIndex = maxChildIndex;
}
}
}
private static void swap(int[] arrays, int heapLength) {
// 将最后一个数据与堆顶数据交换
int temp = arrays[0];
arrays[0] = arrays[heapLength - 1];
arrays[heapLength - 1] = temp;
}
public static void main(String[] args) {
int[] arrays = { 32, 4, 14, 56, 33, 78 };
System.out.println("原数组:" + Arrays.toString(arrays));
HeapSort.sort(arrays);
System.out.println("排序后:" + Arrays.toString(arrays));
}
}
运行结果:
原数组:[32, 4, 14, 56, 33, 78]
数组第1次变动[32, 4, 78, 56, 33, 14]
数组第2次变动[32, 56, 78, 4, 33, 14]
数组第3次变动[78, 56, 32, 4, 33, 14]
数组堆化后:[78, 56, 32, 4, 33, 14]
数组交换堆顶元素后:[14, 56, 32, 4, 33, 78]
数组第4次变动[56, 14, 32, 4, 33, 78]
数组第5次变动[56, 33, 32, 4, 14, 78]
数组堆化后:[56, 33, 32, 4, 14, 78]
数组交换堆顶元素后:[14, 33, 32, 4, 56, 78]
数组第6次变动[33, 14, 32, 4, 56, 78]
数组堆化后:[33, 14, 32, 4, 56, 78]
数组交换堆顶元素后:[4, 14, 32, 33, 56, 78]
数组第7次变动[32, 14, 4, 33, 56, 78]
数组堆化后:[32, 14, 4, 33, 56, 78]
数组交换堆顶元素后:[4, 14, 32, 33, 56, 78]
数组第8次变动[14, 4, 32, 33, 56, 78]
数组堆化后:[14, 4, 32, 33, 56, 78]
数组交换堆顶元素后:[4, 14, 32, 33, 56, 78]
排序后:[4, 14, 32, 33, 56, 78]
整个排序过程中节点变动过程上边也已经打印出来,和之前画的图一一印证,自己可以测试下
按维基百科上的实现如下,本质上相同,读者可以参考下:
public class HeapSort {
/**
* 堆排序数组
*/
private int[] arrays;
/**
* 数组变动次数,只是为了记录
*/
private static int time = 0;
public HeapSort(int[] arrays) {
this.arrays = arrays;
}
public void sort() {
// 1.将数组堆化
// 从第一个非叶子节点length >> 1 - 1开始,叶子节点不需要堆化调整
// maxHeapify 调整index处及其子节点满足堆的特性
int length = arrays.length - 1;
for (int index = arrays.length >> 1 - 1; index >= 0; index--) {
maxHeapify(index, length);
}
// 第一次初始化堆之后的数组:
System.out.println("初始化堆后的数组:" + Arrays.toString(arrays));
// 2.堆化数据排序
// 先将已经堆化的数据堆顶数据(数组索引为0)与堆中最后一个元素交换
// 交换完毕后对剩余节点重新堆化
// 循环执行
for (int i = length; i > 0; i--) {
swap(0, i);
System.out.println("交换堆顶元素后数组:" + Arrays.toString(arrays));
maxHeapify(0, i - 1);
}
}
private void maxHeapify(int index, int length) {
// (index << 1) + 1 为当前节点左子节点索引
// leftChildIndex + 1 为当前节点右子节点索引
int leftChildIndex = (index << 1) + 1;
int rightChildIndex = leftChildIndex + 1;
// 子节点中最大值的索引,默认左子节点
int maxChildIndex = leftChildIndex;
// 左子节点已经超过堆化数组的长度,直接返回
if (leftChildIndex > length) {
return;
}
// 右子节点对应值比左子节点大,则替换maxChildIndex
if (rightChildIndex <= length && arrays[rightChildIndex] > arrays[leftChildIndex]) {
maxChildIndex = rightChildIndex;
}
// 判断是否需要交换
if (arrays[index] < arrays[maxChildIndex]) {
// 交换父子节点
swap(index, maxChildIndex);
// 这里主要是打印日志查看变化过程
time++;
System.out.println("数组第" + time + "次变动" + Arrays.toString(arrays));
// 交换之后对子节点位置进行maxHeapify操作,使其保持堆特性
maxHeapify(maxChildIndex, length);
}
}
private void swap(int a, int b) {
// 数组数据交换
int temp = arrays[b];
arrays[b] = arrays[a];
arrays[a] = temp;
}
public static void main(String[] args) {
int[] arrays = { 32, 4, 14, 56, 33, 78 };
System.out.println("原数组:" + Arrays.toString(arrays));
new HeapSort(arrays).sort();
System.out.println("排序后:" + Arrays.toString(arrays));
}
}
总结
总体而言,堆排序并不是很复杂,也不是很难理解,很多新人可能去死记这个算法,其实并不需要,首先从名字可以看出来最重要的在于‘堆’这个字,当使用这个排序时,我们想一想这个堆的特性,记住这个特点就可以自己动手实现,重要的在于理解其实现的过程
时间复杂度和空间复杂度这里我就不说明了,不过这个复杂度还是需要自己找资料去理解为什么是这个值,毕竟我们用这个算法就是因为某些场景适合,复杂度的分析对我们来说很有必要
以上内容如有问题欢迎指出,笔者验证后将及时修正,谢谢
以上是关于算法那些事儿之堆排序的主要内容,如果未能解决你的问题,请参考以下文章