Leecode位运算与堆排序

Posted 2021-05-01 小虾米的数据分析

位运算

常见的位操作包括：

与 &

或  |

非  |

异或 ^

左移 <<

右移 >>

Leecode 136

这一题本质上就是考位运算的，对于异或操作来说，有：
a ^ a = 0
a ^ 0 = a
a ^ b ^ a = a ^ a ^ b = b
然后这题就解决了。

如下图所示：

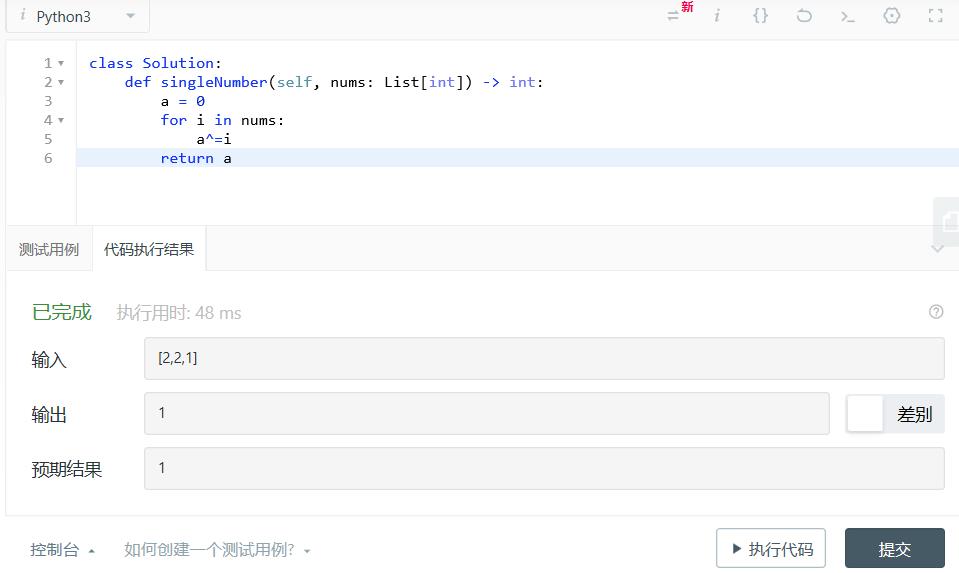
时间复杂度是O(n)，所有num中元素遍历一遍。

空间复杂度是O(1)。

Leecode 260

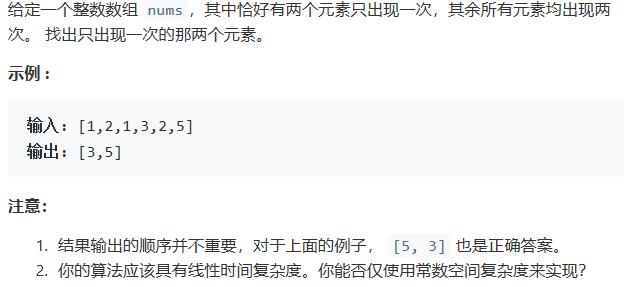
如果仍然用上面位运算的方法，最终得到的是3和5异或的结果。用二进制表示就是：

                      0 0 1 1

                      0 1 0 1

得到的结果是  0 1 1 0

取出来第一位上为1的，表示这两个数在这一位上不同，根据这一位来进行分类后再异或求解。

具体做法如下：

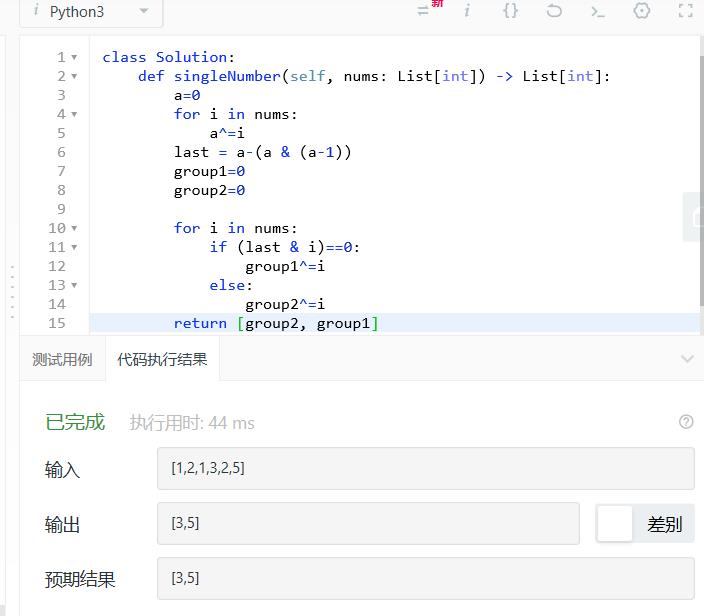
时间复杂度是O(n)。空间复杂度是O(1)。

堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

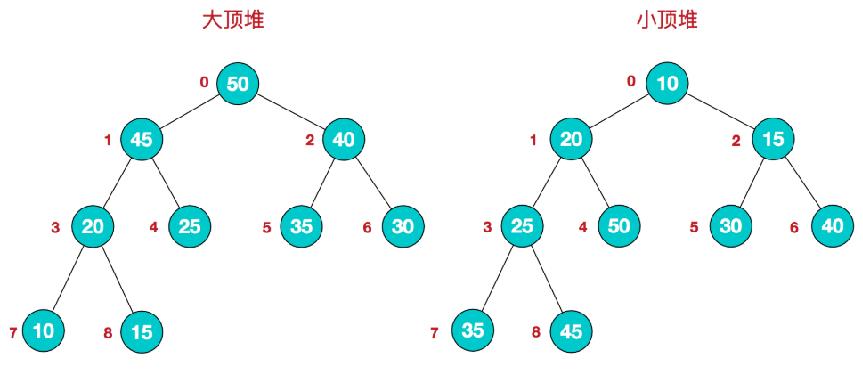
堆不需要用树来存储，可以直接用数组来存，根据完全二叉树的性质，在这个数组中对于当前节点i来说：
左节点为：2i+1
右节点为：2i+2
那么大顶堆有：
arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  
小顶堆有：
arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

堆排序

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

所以为什么大顶堆是升序，而小顶堆是降序，因为大顶堆每次将最大的放到数组末尾，小顶堆也是一样！

举例说明：

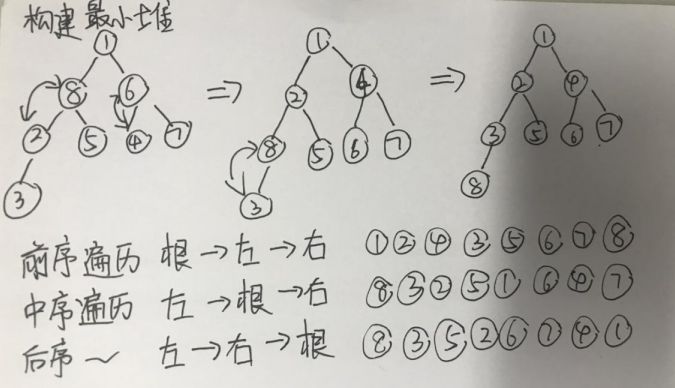
题目：初始序列为1 8 6 2 5 4 7 3的一组数采用堆排序，当建堆(小根堆)完毕时，堆所对应的二叉树中序遍历序列为：( )（英特尔2016软件类研发在线测评）

A、8 3 2 5 1 6 4 7

B、3 2 8 5 1 4 6 7

C、3 8 2 5 1 6 7 4

D、8 2 3 5 1 4 7 6

 

Leecode215. 数组中的第k个最大元素

对于本题来说，我们并不是进行排序，我们是寻找第k大的，所以并不需要排序完，我们进行了k次，就能够找到第K大的元素，所以我们只进行K次。

 

构建大顶堆

：

Python3 完整代码

--------------------------------------------------------------------------

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        return self.heap_sort(nums, k)
   
    def heap_sort(self, nums, k):
        for i in range(len(nums)//2-1, -1, -1):
            self.heap_adjust(nums, i, len(nums))   
        cnt = 0
        for i in range(len(nums)-1, 0, -1):
            self.heap_swap(nums, 0, i)
            cnt+=1
            if cnt == k:
                return nums[i]
            self.heap_adjust(nums, 0, i)
        return nums[0]
   
    def heap_adjust(self, nums, start, length):
        tmp = nums[start]
        k = start*2+1
        while k<length:
            left  = start*2+1
            right = left+1
           
            if right<length and nums[left]<nums[right]:
                k = right
            if nums[k]>tmp:
                nums[start] = nums[k]
                start = k
            else:
                break
            k = k*2+1
        nums[start]=tmp
       
    def heap_swap(self, nums, i, j):
        nums[i],nums[j] = nums[j],nums[i]
        return nums
   
  -------------------------------------------------------------
   

时间复杂度-O(NlogK)，空间复杂度-O(K)。