排序算法专题之堆排序
Posted Python算法之旅
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序算法专题之堆排序相关的知识,希望对你有一定的参考价值。
普通二叉树是不适合使用线性表来存储的,因为会出现大量的闲置空间,但完全二叉树是个例外。使用线性表来存储完全二叉树,不仅不会出现闲置空间,而且还很容易确定孩子结点和双亲结点的位置关系,从而快速对彼此进行定位。
我们可以根据完全二叉树的这个特点,通过反复构造大根堆,来对数组进行排序,这就是堆排序算法。




扫码加入“Python算法之旅”微信群,和斌哥面对面交流,更多资料和更有趣的话题等你一起来分享。
排序算法专题之堆排序
1. 完全二叉树
完全二叉树:除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。
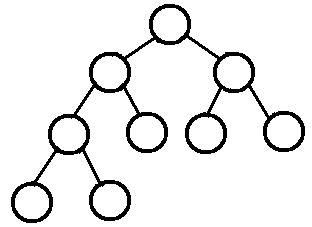
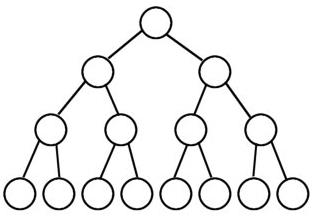
满二叉树:除了叶子结点之外的每一个结点都有两个孩子,每一层都被完全填充。
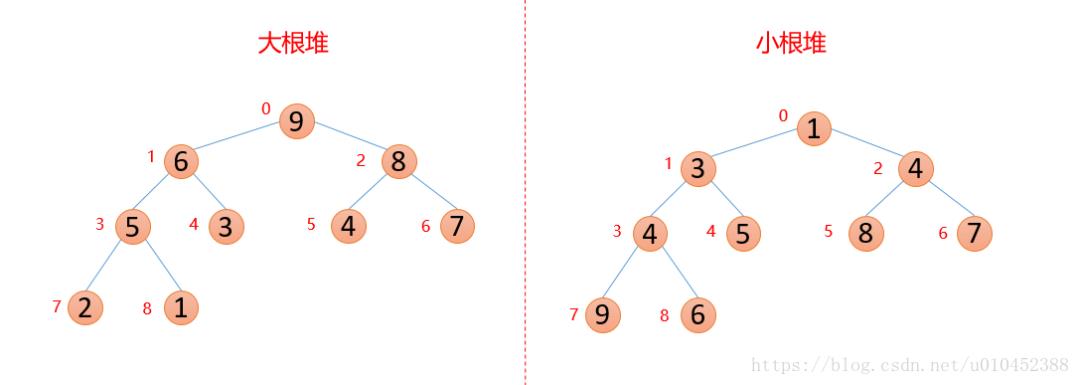
2. 大根堆和小根堆
堆是一棵顺序存储的完全二叉树。
其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为大根堆。
3. 构造大根堆
方法一:通过不断插入新元素,对新元素做向上调整操作,得到新的大根堆。
函数名:create_max_heap(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会将列表改造成大根堆。
def create_max_heap_2(a):
#通过不断插入新元素,对新元素做向上调整操作,将一个普通数组改造成大根堆
for i in range(2, len(a)+1):
sift_up(a, len(a), i)
#向上调整二叉堆的第pos个元素a[pos-1],使其满足大根堆的特征
def sift_up(a, n, pos):
temp = a[pos-1] #第pos个元素的值
parents = pos // 2 #指向双亲结点
while parents > 0:
if a[parents-1] < temp: #通过向下移动双亲结点值的方式,确保双亲大于孩子
a[pos-1] = ①
pos = ②
parents = pos // 2
else:
break
a[pos-1] = ③ #将temp向上调整到适当位置
方法二:通过逆序向下调整非叶子结点,将一个普通数组改造成大根堆。
函数名:create_max_heap(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会将列表改造成大根堆。
def create_max_heap(a):
#通过逆序向下调整非叶子结点,将一个普通数组改造成大根堆
for i in range(len(a)//2, 0, -1):
sift_down(a, len(a), i)
#向下调整二叉堆的第pos个元素a[pos-1],使其满足大根堆的特征
def sift_down(a, n, pos):
temp = a[pos-1] #第pos个元素的值
child = pos * 2 #指向左孩子a[child-1]
while child <= n:
if child < n and a[child-1] < a[child]: #有右孩子,且右孩子更大些,定位其右孩子
child += 1 #指向右孩子
if a[child-1] > temp: #通过向上移动孩子结点值的方式,确保双亲大于孩子
a[pos-1] = ①
pos = ②
child = pos * 2
else:
break
a[pos-1] = ③ #将temp向下调整到适当位置
4. 堆排序
堆排序基本思想:
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
函数名:heap_sort(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会对列表的对象进行升序排序。
def heap_sort(a):
create_max_heap(a) #先构造一个大根堆
for i in range(len(a)-1, 0, -1):
a[0], a[i] = a[i], a[0]
sift_down(① ) #对根结点向下调整,得到长度为i的新大根堆3. 构造大根堆
方法一:通过不断插入新元素,对新元素做向上调整操作,得到新的大根堆。
函数名:create_max_heap(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会将列表改造成大根堆。
def create_max_heap_2(a):
#通过不断插入新元素,对新元素做向上调整操作,将一个普通数组改造成大根堆
for i in range(2, len(a)+1):
sift_up(a, len(a), i)
#向上调整二叉堆的第pos个元素a[pos-1],使其满足大根堆的特征
def sift_up(a, n, pos):
temp = a[pos-1] #第pos个元素的值
parents = pos // 2 #指向双亲结点
while parents > 0:
if a[parents-1] < temp: #通过向下移动双亲结点值的方式,确保双亲大于孩子
a[pos-1] = a[parents-1]
pos = parents
parents = pos // 2
else:
break
a[pos-1] = temp #将temp向上调整到适当位置
方法二:通过逆序向下调整非叶子结点,将一个普通数组改造成大根堆。
函数名:create_max_heap(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会将列表改造成大根堆。
def create_max_heap(a):
#通过逆序向下调整非叶子结点,将一个普通数组改造成大根堆
for i in range(len(a)//2, 0, -1):
sift_down(a, len(a), i)
#向下调整二叉堆的第pos个元素a[pos-1],使其满足大根堆的特征
def sift_down(a, n, pos):
temp = a[pos-1] #第pos个元素的值
child = pos * 2 #指向左孩子a[child-1]
while child <= n:
if child < n and a[child-1] < a[child]: #有右孩子,且右孩子更大些,定位其右孩子
child += 1 #指向右孩子
if a[child-1] > temp: #通过向上移动孩子结点值的方式,确保双亲大于孩子
a[pos-1] = a[child-1]
pos = child
child = pos * 2
else:
break
a[pos-1] = temp #将temp向下调整到适当位置
4. 堆排序
堆排序基本思想:
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
函数名:heap_sort(a)
参数表:a -- 待排序列表。
返回值:该方法没有返回值,但是会对列表的对象进行升序排序。
def heap_sort(a):
create_max_heap(a) #先构造一个大根堆
for i in range(len(a)-1, 0, -1):
a[0], a[i] = a[i], a[0]
sift_down(a, i, 1) #对根结点做向下调整操作,得到长度为i的新大根堆Python排序算法系列文章是我在阅读了大量算法专著以后,尝试用浅陋的语言把自己的理解表达出来。由于本人水平有限,表述中难免出现疏漏甚至错误之处,敬请谅解。
无论是赞同还是反对我的看法,都请你给我留言。如果你有新的想法,千万不要憋在心里,请发出来大家一起讨论。让我们相互学习,共同进步!
需要本文word版的,可以加入“选考VB算法解析”知识星球参与讨论和下载文件,“选考VB算法解析”知识星球汇集了数量众多的同好,更多有趣的话题在这里讨论,更多有用的资料在这里分享。
我们专注选考VB算法,感兴趣就一起来!
相关优秀文章:
以上是关于排序算法专题之堆排序的主要内容,如果未能解决你的问题,请参考以下文章