堆排序(最大堆)

Posted 2021-05-01 Java编程生涯

一、定义和性质

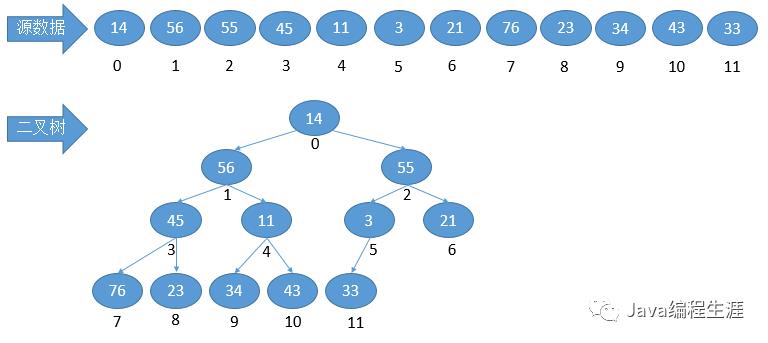
定义：堆是按照完全二叉树的顺序结构存储在一个一维数组中，逻辑存储是完全二叉树，物理存储是数组。

性质：具有完全二叉树的顺序结构特性。

           对于任意的节点，从上往下，父节点都大于左孩子和右孩子。

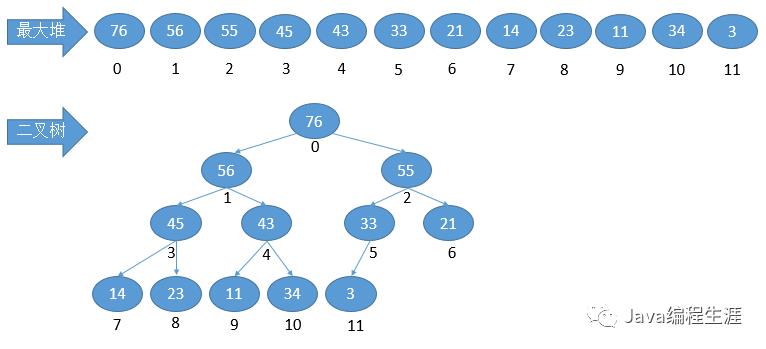
           根节点最大的情况，称为最大堆。

用数组存储二叉堆，堆的顶点下标可以从0开始也可以从1开始。

堆顶下标从0开始：父节点=(i-1)/2、左子节点=2*i+1、右子节点=2*i+2，根节点等于0。

堆顶下标从1开始：父节点=i/2、左子节点=2*i、右子节点=2*i+1，根节点等于1。

调整原理：围绕最后一个叶子节点开始调整，也就是从33开始调整。

源数据图形：

最大堆图形：

二、排序源码

1、初始化

import java.util.Arrays;

/**
 * 堆排序(最大堆)
 * 计算方式: 父节点为(i-1)/2
 *          左子节点为2*i+1
 *          右子节点为2*i+2
 * @author ouyangjun
 */
public class MaxHeap {

    private int[] elementData;
    private int size;

    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

    // 默认初始容量
    public MaxHeap() {
        this(8);
    }

    // 指定初始容量
    public MaxHeap(int initialCapacity) {
        if (initialCapacity > 0) {
            elementData = new int[initialCapacity];
        } else {
        throw new IllegalArgumentException("Illegal Capacity: "+
                                               initialCapacity);
        }
    }

    /**
     * 扩容
     * @param minCapacity
     */
    private void grow(int minCapacity) {
        if (minCapacity - elementData.length > 0) {
            int oldCapacity = elementData.length;
            int newCapacity = oldCapacity + (oldCapacity >> 1);
            if (newCapacity - minCapacity < 0) {
                newCapacity = minCapacity;
            }
            if (newCapacity - MAX_ARRAY_SIZE > 0) {
                if (minCapacity < 0) {
                    throw new OutOfMemoryError(); 
                }
                newCapacity = minCapacity > MAX_ARRAY_SIZE ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;
            }
            elementData = Arrays.copyOf(elementData, newCapacity);
        }
    }

    // 父节点
    private int parent(int n) {
        return (n-1)/2;
    }

    // 左子节点
    private int left(int n) {
        return 2 * n + 1;
    }

    // 右子节点
    private int right(int n) {
        return 2 * n + 2;
    }

}

2、调整最大堆

/**
  * 向上调整为最大堆, 向上调整只需要考虑双亲结点
  * @param array
  */
private void upMaxHeap(int[] array, int length) {

    // 找到最后一个叶子节点的父节点
    int parentIndex = parent(length);
    for (int i = parentIndex; i >= 0; i--) {
        upMaxHeap(array, i, length);
    }
}

private void upMaxHeap(int[] array, int index, int length) {
    // 先把第一个左孩子作为最大值
    int max = left(index);

    while (max < length) {
        if (max + 1 < length && array[max + 1] > array[max]) {
            max += 1;
        }

        if (array[index] >= array[max]) {
            break;
        }

        int t = array[max];
        array[max] = array[index];
        array[index] = t;

        index = max;
        max = left(index);
    }
}

3、添加

// 添加
public void add(int value) {
    // 判断是否需要扩容
    grow(size + 1);

    // 插入元素
    elementData[size++] = value;

    // 调整成最大堆
    upMaxHeap(elementData, size);
}

// 打印
public void print() {
    System.out.print("[");
    for (int i = 0; i < size; i++) {
        System.out.print(elementData[i] + ", ");
    }
    System.out.print("]");
}

4、main方法测试

public static void main(String[] args) {
    MaxHeap heap = new MaxHeap();
    heap.add(14);
    heap.add(56);
    heap.add(55);
    heap.add(45);
    heap.add(11);
    heap.add(3);
    heap.add(21);
    heap.add(76);
    heap.add(23);
    heap.add(34);
    heap.add(43);
    heap.add(33);
    // 打印
    heap.print();

}

未

完

待

续

纸上得来终觉浅，绝知此事要躬行。

--陆游《冬夜读书示子聿》