不基于比较的基数排序原理图解

Posted 2021-05-01 Python与算法社区

主要推送关于对算法的思考以及应用的消息。坚信学会如何思考一个算法比单纯地掌握100个知识点重要100倍。本着严谨和准确的态度，目标是撰写实用和启发性的文章，欢迎您的关注，让我们一起进步吧。

01

—

你会学到什么？

彻底弄明白常用的排序算法的基本思想，算法的时间和空间复杂度，以及如何选择这些排序算法，确定要解决的问题的最佳排序算法，已经总结了，，，。

02

—

讨论的问题是什么？

各种排序算法的基本思想；讨论各种排序算法的时间、空间复杂度；以及算法的稳定性；算法是如何改进的，比如冒泡排序如何改进成了目前最常用的快速排序的，直接选择排序到堆排序的改进，直接插入排序到希尔排序做的优化，归并排序，这些算法都是基于数的比较和移动思想。

下面讨论的基数排序算法，，不基于数的比较和移动思想，而是基于分配式思想。

03

—

相关的概念和理论

在讨论时假定关键码为数值型，这只是为了讨论的方便，基数排序应用的场景更可能是非数值型。

关键码位数

待排序序列中最大数的位数，例如序列 [2, 10, 8, 234]，关键码为：0,1,2,3,4,8，关键码位数 d 为6 。如果关键码是数值型的那么上限为 10个。

radix

关键码的取值范围，例如序列 [2, 10, 8, 234]，按照从右数的顺序第一位d1=1时的关键码的取值为 4,8,0,2，即范围为0~8 。

记录数

待排序的个数

桶

基数排序中，桶的编号为关键码的取值。若关键码为数值型，则桶的编号为0~9，共10个不同的桶。

分配

将记录按照某位（比如从右往左数第1位）将记录分配到编号为0~10的桶中的过程。比如 [2, 10, 8, 234]第一次分配（第一次分配定义为按照从右往左数的第1位）后，桶0中有10，桶2中有2，桶4中有234，桶8中8，其他桶，比如1,3,5,6,7,9桶中都没有记录。

收集

分配后需要对桶中的记录再串起来，这个过程叫做收集。比如，上面的序列收集后的结果为（按照从桶0到桶9的顺序收集）10, 2，234，8 。

稳定排序

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序后，这些记录的相对次序保持不变，即在原序列中 ri=rj， ri 在 rj 之前，而在排序后的序列中，ri 仍在 rj 之前，则称这种排序算法是稳定的；否则称为不稳定的。

04

—

基数排序思想

基数排序（radix sort），属于“分配式排序”（distribution sort）。

基数排序算法先要求计算出待排序序列的最大位数，将记录切割成不同的数字，按照最高位优先或者最低位优先的规则遍历（请看下面的注释）；

每次遍历中：

1. 分配。首先要将待排序序列中的当前位上的数字找到对应的桶；

2. 收集。分配后需要对桶中的记录再串起来，形成一个新的排序序列，供下一次分配用。

直至遍历完成，得到排序好的序列。

最高位优先 (Most Significant Digit first)法，简称MSD法：先按key = 1 排序分组，再对各组按k = 2 排序分成子组，对后面的关键码继续这样的排序分组，直到按最右位关键码 k = d对各子组排序后。

最低位优先 (Least Significant Digit first)法，简称LSD法：先从k = d开始排序，再对k = d-1进行排序，依次重复，直到对k = 1排序后便得到一个有序序列。

05

—

例子

假定待排序的序列为 22, 33, 43, 55, 14, 28, 65, 39, 81, 33, 100 。

假定按照LSD法，即最低位优先原则，对以上序列进行非降序排序。

显然，这个序列的最大关键码位数为3 。

第一次分配如下图所示，22的最低位为2，所以被分配到桶2中，33的最低位为3，所以被分配到桶3中，43的最低位为3，所以被分配到桶3中，依次类推，100的最低位为0，所以被分配到桶0中。

可以看出，桶7和桶8都没有被分配记录，所以在图中没有画出。

然后进行采集操作，采集的过程就是串联的过程，如上图所示，经过这次采集得到新序列为 100, 81, 22, 33, 43, 33, 14, 55, 65, 28, 39 。

接下来，对新序列进行第二次分配和采集，即按照从最右侧开始的第二位的顺序分配，如下图所示，此时得到的新序列为 100， 14， 22， 28，33, 33，39， 43， 55， 65， 81  。

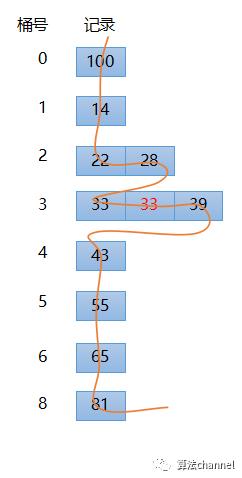
接下来，对最新的序列进行第三次分配和采集，即按照从最右侧开始的第三位的顺序分配，如下图所示，因为一共就只有一个数100是3位数，所以其他的数都依次被分配到桶0中，桶1中含有100 。

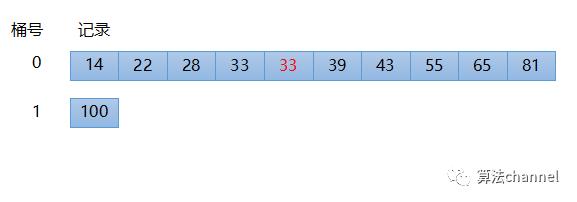
最后再将这些数采集起来，如下图所示，此时得到的序列为 14， 22， 28，33, 33，39， 43， 55， 65， 81， 100 。可以看到100的空间位置从位置0直接挪动到最后。

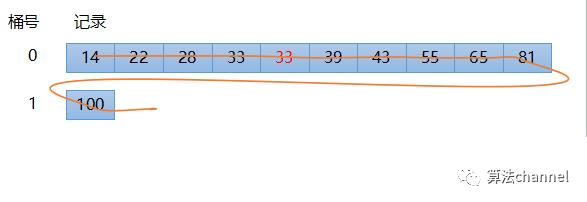
至此在这个序列中，关键码数已经等于3，也就是说算法已经结束，我们得到了最终的排序好的非降序序列。

再想想基数排序，因为桶的顺序已经按照0~9顺序，按照位拆分后，每位都相当于有一个权重的大小，从最低位到最高位，权重越来越大。

可以看到相等码33的顺序没有发生改变，并且这并不是巧合，所以说基数排序是稳定的排序算法。

因为每个桶内的元素个数是未知的，所以需要借助链表结构来实施分配时向桶内仍记录的过程。

06

—

算法评价

借助桶编号（键）经过多次分配和采集，最终得到一个有序序列，在这个算法排序过程中，没有经过任何记录的比较，因此基数排序是很独特的排序算法。

待排序列为n个记录，d个关键码，关键码的取值范围为radix，其中，一趟分配

时间复杂度为 O(n)，一趟收集时间复杂度为O(radix)，共进行d趟分配和收集，所以链式基数排序的时间复杂度为 O(d · (n+radix) ) 。

注意这不是说这个时间复杂度一定优于O(n·log(n))，因为 d 的大小一般会受到 n 的影响。 

采用链表或线性数组存储n个记录，自然地每个记录在每趟分配的时候需要临时申请一个内存空间记录下来，此时需要的空间复杂度为O(n)；并且，每次分配时，每个桶中可能含有多条记录，每个桶再形成一个链表，再占用额外的内存空间 。

07

—

特殊性

很多书上对基数排序的阐述都是针对数值排序，包括我们上面的举的那个例子，也是针对数值排序的，但是仔细想想数值的大小是已知的，如果再将数值按位拆分再排序，有时候是没有必要的。而算法的目的是找到最佳解决问题的方案，而不是把简单的事搞的更复杂。

基数排序主要的应用在哪里呢？ 目前未得到很好的验证，等以后有了想法再来补充。

08

—

总结

借助桶编号（键）经过多次分配和采集，最终得到一个有序序列，基数排序算法独树一帜，不像之前总结的排序算法，比如，，，等，实质上都要基于数的比较和移动。

基数排序的缺点是不呈现时空的局部性，因为在按位对每个数进行排序的过程中，一个数的位置可能发生巨大的变化，所以不能充分利用现代机器缓存提供的优势。

同时基数排序不具有原地排序的特点，占用一定的内存空间，当内存容量比较宝贵的时候，还是有待商榷。

另外，基数排序的应用场景有待考证。