每日一算法|基数排序---第十一天

Posted 2021-05-01 江小湖资源分享平台

基数排序

算法

原理

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

基数相对于前面的排序稍微复杂些，原理与桶排序类似，可以分为高位优先和低位优先。我们这里讲低位优先，高位一样的理解就好。

基数排序适合对那些位数差别比较大的数组适用性会好些。以整数排序为例，主要思想是将整数按位数划分，准备 10 个桶，代表 0 - 9，根据整数个位数字的数值将元素放入对应的桶中，之后按照输入赋值到原序列中，依次对十位、百位等进行同样的操作，最终就完成了排序的操作。

我们要找出最大值，判断它是多少位的我们就循环多少次。

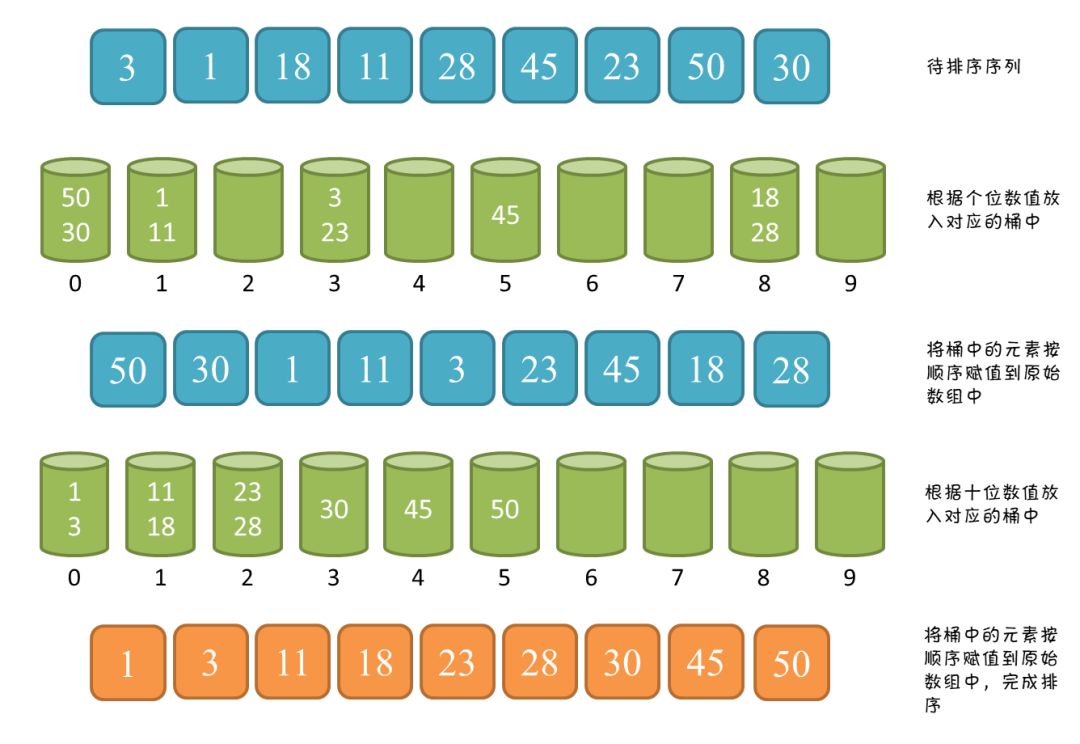
接下来举例说明一下，假设有一组数据{3,1,18,11,28,45,23,50,30}，最大位数为两位，所以只要循环两次就行了。

第一步：准备0~9的10个空桶（分配空间），把上面的数据按个位分别放到对应的空桶（空间）中，放完后，将空桶中的数据按顺序放回原来的数组中去，这样第一趟就完成了。

第二步：按十位把数组放到对应空桶（空间）中，十位没有的按0来算；全部放好后再按顺序放回到原来数组中，此时，数列排序完毕。

如果还有更多位数的数，按上面的方法依次把位数往前推就好。

总结一下：

1.找最大值，判断位数。

2.位数=循环次数

3.分配空间

4.使用二维数组存储元素在桶中的位置：一个是余数位，一个是在在桶中第几个位置。

C语言

#include<stdio.h>
 
#define Max_ 10      //数组个数
#define RADIX_10 10    //整形排序
#define KEYNUM_31 10     //关键字个数，这里为整形位数
 
// 打印结果
void Show(int  arr[], int n)
{
    int i;
    for ( i=0; i<n; i++ )
        printf("%d  ", arr[i]);
    printf("\n");
}
 
// 找到num的从低到高的第pos位的数据
int GetNumInPos(int num,int pos)
{
    int temp = 1;
    for (int i = 0; i < pos - 1; i++)
        temp *= 10;
    
    return (num / temp) % 10;
}
 
 
//基数排序  pDataArray 无序数组；iDataNum为无序数据个数
void RadixSort(int* pDataArray, int iDataNum)
{
    int *radixArrays[RADIX_10];    //分别为0~9的序列空间
    for (int i = 0; i < 10; i++)
    {
        radixArrays[i] = (int *)malloc(sizeof(int) * (iDataNum + 1));
        radixArrays[i][0] = 0;    //index为0处记录这组数据的个数
    }
    
    for (int pos = 1; pos <= KEYNUM_31; pos++)    //从个位开始到31位
    {
        for (int i = 0; i < iDataNum; i++)    //分配过程
        {
            int num = GetNumInPos(pDataArray[i], pos);
            int index = ++radixArrays[num][0];
            radixArrays[num][index] = pDataArray[i];
        }
        
        for (int i = 0, j =0; i < RADIX_10; i++)    //收集
        {
            for (int k = 1; k <= radixArrays[i][0]; k++)
                pDataArray[j++] = radixArrays[i][k];
            radixArrays[i][0] = 0;    //复位
        }
    }
}
 
int main()
{   //测试数据
    int arr_test[Max_] = { 3,1,18,11,28,45,23,50,30 };
    //排序前数组序列
    Show( arr_test, Max_ );
    RadixSort( arr_test, Max_);
    //排序后数组序列
    Show( arr_test, Max_ );
    return 0;
}

Java

// 基数排序
public static void radixSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
    
// 计算最大位数
public static int maxbits(int[] arr) {
    int max = Integer.MIN_VALUE;
    for (int i = 0; i < arr.length; i++) {
        max = Math.max(max, arr[i]);
    }
    int res = 0;
    while (max != 0) {
        res++;
        max /= 10;
    }
    return res;
}

// 基数排序
public static void radixSort(int[] arr, int begin, int end, int digit) {
    final int radix = 10;
    int i = 0, j = 0;
    int[] count = new int[radix];
    int[] bucket = new int[end - begin + 1];
    // 依次遍历每个位数
    for (int d = 1; d <= digit; d++) {
        for (i = 0; i < radix; i++) {
            count[i] = 0;
        }
            
        // 统计数量
        for (i = begin; i <= end; i++) {
            j = getDigit(arr[i], d);
            count[j]++;
        }
            
        // 计算位置
        for (i = 1; i < radix; i++) {
            count[i] = count[i] + count[i - 1];
        }
            
        // 记录到对应位置
        for (i = end; i >= begin; i--) {
            j = getDigit(arr[i], d);
            bucket[count[j] - 1] = arr[i];
            count[j]--;
        }
        for (i = begin, j = 0; i <= end; i++, j++) {
            arr[i] = bucket[j];
        }
    }
}

// 获取位数数值
public static int getDigit(int x, int d) {
    return ((x / ((int) Math.pow(10, d - 1))) % 10);
}

Python

def RadixSort(a):
    i = 0                                             #初始为个位排序
    n = 1                                           #最小的位数置为1（包含0）
    max_num = max(a)                       #得到带排序数组中最大数
    while max_num > 10**n:              #得到最大数是几位数
        n += 1
    while i < n:
        bucket = {}                             #用字典构建桶
        for x in range(10):
            bucket.setdefault(x, [])    #将每个桶置空
        for x in a:                               #对每一位进行排序
            radix =int((x / (10**i)) % 10)   #得到每位的基数
            bucket[radix].append(x) #将对应的数组元素加入到相应位基数的桶中
        j = 0
        for k in range(10):
            if len(bucket[k]) != 0:       #若桶不为空
                for y in bucket[k]:         #将该桶中每个元素
                    a[j] = y                       #放回到数组中
                    j += 1
        i += 1

if __name__ == '__main__':
    a = [3,1,18,11,28,45,23,50,30]
    print("Before sorting...")
    print("---------------------------------------------------------------")
    print(a)
    print("---------------------------------------------------------------")
    RadixSort(a)
    print("After sorting...")
    print("---------------------------------------------------------------")
    print(a)
    print("---------------------------------------------------------------")

总结：排序算法到这里就讲完了，总共十大排序算法，当然还有一些其他的排序算法，这里就不发了。之后会做一个总结，对比一下10大经典排序算法各个方面的区别、优劣等。

         再之后的算法，也是一些比较经典的算法，还有蓝桥杯的一些试题解析（当然，看得懂就发，看不懂就算了（手动狗头.jpg））。