BokehMe: When Neural Rendering Meets Classical Rendering
Posted spearhead_cai
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BokehMe: When Neural Rendering Meets Classical Rendering相关的知识,希望对你有一定的参考价值。
论文地址:https://openaccess.thecvf.com/content/CVPR2022/papers/Peng_BokehMe_When_Neural_Rendering_Meets_Classical_Rendering_CVPR_2022_paper.pdf
代码地址:https://github.com/JuewenPeng/BokehMe

摘要
我们提出了 BokehMe,这是一个混合的虚化渲染框架,将神经渲染器与经典的物理驱动渲染器结合在一起。给定单个图像和可能不完美的视差图,BokehMe 可以生成具有可调节的模糊大小、焦平面和光圈形状的高分辨率照片般逼真的虚化效果。为此,我们分析了经典的基于散射的方法的误差,并推导出计算误差图的公式。基于这个公式,我们通过基于散射的方法实现了经典渲染器,并提出了一种两阶段神经渲染器来修复经典渲染器中的错误区域。神经渲染器采用动态多尺度方案来有效处理任意模糊大小,并经过训练以处理不完美的视差输入。实验表明,我们的方法在具有预测视差的合成图像数据和真实图像数据上都优于以前的方法。进一步进行用户研究以验证我们方法的优势。
1. 介绍
虚化(bokeh)效果指的是镜头在照片中呈现焦外模糊的方式,如下图 1 所示。通过不同的镜头设计和配置,可以创造各种虚化风格。例如,光圈可以控制虚化球的形状。经典渲染方法[6,20,31,40]可以通过控制模糊核的形状和大小来轻易改变虚化的风格。但是它们的缺点是在深度不连续处会有伪影。神经渲染方法[11,25,32]通过从图像统计中学习来处理这个问题,不过它们的问题是很难模拟真实的虚化球并且仅能产生训练数据中的虚化风格。另外,之前的神经渲染方法缺乏在高分辨率图片上产生大模糊大小的机制,原因是神经网络固定的感受野以及受限于训练数据的模糊大小。

为了实现没有伪影以及高度可控的虚化效果,我们提出了一个新的混合框架,命名为 BokehMe,它通过融合经典渲染器和神经渲染器的结果来充分利用各自的优点,如下图 2 。我们将基于散射的方法[31]作为我们的经典渲染器。为了确定这种方法可能在哪个区域渲染出明显的边界伪影,我们对镜头系统进行了建模,并对基于散射的渲染和真实渲染之间的误差进行了综合分析。求导出一个软但紧密的误差图,可以用于识别带有边界伪影的区域。采用这个误差图将伪影区域替换为神经渲染的结果,我们可以保留经典渲染器的虚化风格而又不会出现明显的视觉伪影。对于神经渲染器,为了打破模糊大小限制,我们将其分解为两个子网络:自适应渲染网络(ARNet)和迭代上采样网络(IUNet)。 在 ARNet 中,我们自适应地调整输入图像的大小并生成低分辨率的虚化图像。 然后,IUNet 则是基于初始的高分辨率输入图像迭代引导的对低分辨率虚化图像进行上采样。 因此,我们的神经渲染器可以处理任意大的模糊大小。

本文的主要贡献总结如下:
- 我们提出了一个结合一个经典渲染器和一个神经渲染器的新框架,从而实现逼真的和高度可控的虚化渲染;
- 我们分析了镜头系统然后提出了一个误差图公式来有效的融合经典渲染和神经渲染;
- 我们提出了一个两阶段的神经渲染器,它采用自适应调整大小以及迭代上采样方法来对高分辨率图片处理任意的模糊大小,并且它对可能不完美的视差输入比较鲁棒;
另外,由于在可控虚化渲染领域缺乏测试数据,我们贡献了一个新的 benchmark:BLB,由Blender 2.93 [5]合成,与EBB400一起,从 EBB! [11]中处理所得。 由于虚化效果的评估具有主观性,因此我们还对 iPhone 12 拍摄的图像进行了用户研究。大量结果表明,BokehMe 可以渲染出逼真的图像并保持虚化风格的多样性。
2. 相关工作
经典渲染器。经典渲染可以分为两类:对象空间方法和图像空间方法。对象空间方法[1,16,33,39]基于光线追踪可以渲染精确的结果,但大部分都非常耗时而且需要完整的 3D 场景信息,因此并不实用。相比之下,图像空间方法[3,4,10,29,38]仅需要一张图片和对应的深度图,这都非常容易实现。最近这几年,越来越多的方法[6,20,23,27,28,31,34,40]结合了不同的模块,比如深度估计,语义分割以及经典渲染,来构建一个自动渲染的系统。为了防止背景颜色渗入前景,大多数方法根据估计的深度图将图像分解为多个层,并从后向前执行渲染。
尽管经典渲染是灵活的,但这种范式在深度不连续处存在伪影,尤其是当焦平面以背景为目标时。
神经渲染器。为了提高效率和避免边界伪影,最近也有很多工作采用神经网络来模拟渲染处理。比如,Nalbach 等人[21]和 Xiao 等人[35] 采用清晰图片和对应完美的深度图来训练网络实现虚化效果。通过对 OpenGL 着色器和 Unity 引擎 [30] 创建的合成数据进行训练,可以有效地缓解边界伪影。 然而,在现实世界中并不总是很容易获得完美的深度图。 王等人 [32] 因此提出了一种自动渲染系统,包括深度预测、镜头模糊和引导上采样,以从单个图像生成高分辨率景深 (DoF) 图像。 此外,最近还研究了编码器-解码器网络 [9,11–13,25],它以端到端的方式将全焦点图像映射到浅景深图像。 与上述方法不同,Xu 等人[37]专注于全自动肖像渲染。 他们使用循环过滤器 [18] 来近似基于条件随机场的渲染方法,并实现显着的速度提升。
然而,神经渲染的主要问题是缺乏控制能力。对一个训练好的神经网络,虚化风格无法改变并且模糊范围也是有限的。另外,网络产生的虚化球是不真实的,因为网络会倾向于学习简单的模糊效果。
3. BokehMe:一个混合的渲染框架
如下图 3 所示,我们的框架通过输入一张清晰图片 I,一张视差图 D 以及由两个渲染器:经典渲染器和神经渲染器控制的参数生成一张虚化图片 B。他们的渲染结果基于一个误差图 E 进行融合,该误差图 E 从经典渲染器中识别出潜在的错误区域。控制参数包括模糊参数 K、重聚焦视差 d f d_f df、伽马值 γ 和一些关于散景风格的参数,例如光圈形状 . 具体而言,K反映了整个图像的模糊量。 df 确定焦平面的视差(反深度)。 γ,用于伽马校正,控制虚化球的亮度和显着性。

3.1 经典渲染器和误差分析
经典渲染器。我们期望经典渲染器在深度连续区域渲染真实的虚化效果。在对比了不同的方法后,我们发现基于散射的逐像素渲染方法[23,31]在深度不连续处也会有严重的渗色伪影,但在这些区域的误差相对较小。该方法的核心思想是将每个像素分散到其相邻区域,它们之间的距离小于像素的模糊半径。 如 [31, 38] 中所讨论的,给定像素的视差 d,其模糊半径可以通过下式计算:

我们采用 CuPy 包来实现算法,这可以实现显著的并行速度提升(参考补充材料)。由于从场景辐照度到图像强度的转换是非线性的 [38],因此在渲染之前和之后应用了额外的伽马校正 [17]。
镜头系统。为了理解为什么基于散射的方法会导致深度不连续处的误差,我们建模了一个虚拟透镜系统。 对于空间中存在两个对象的简单场景(图 4),我们在深度不连续处推导出 8 个渲染案例(此处显示了 2 个案例,而其他案例显示在补充材料中)。 以中心像素(黑点)为例,只有红色的梯度前景平面上的相邻像素和蓝色的梯度背景平面上的相邻像素才能传递到中心像素。 显然,基于散射的渲染与真实渲染不同。

初始的误差图。我们的目标是获得一个错误图来识别经典渲染器错误渲染的区域。 稍后,我们将训练一个神经网络来预测本节中制定的误差图。 让 E∗ 表示目标误差图。 由于只有深度边界的散射半径内的区域可能与真实渲染有显着差异,因此 E* 可以保守地表示为深度边界的空间变膨胀,膨胀大小取决于最大模糊半径 位于深度边界两侧的像素。 以图 4 中的场景为例,E∗ 的第 i 个元素可以定义为

其中 α i \\alpha_i αi 可以看作是 E i ∗ E^*_i Ei∗ 的一个变量, i ′ i^' i′ 是另一个深度平面的第 i 个像素最近像素的索引。 l i i ′ l_ii^' lii′ 是两个像素的距离。 r i r_i ri 和 r i ′ r_i^' ri′ 是对应像素的模糊核半径。
改进的误差图。考虑到经典渲染器在深度连续区域中可以生成可控虚化风格的高质量结果的事实,我们希望适当地缩小和软化初始误差图,以在融合边界保留更多来自经典渲染器的散景结果并且没有明显的伪影。
通过补充材料中显示的理论和数值分析,我们得出对于每个像素,基于散射的渲染结果与真实渲染结果之间的色差为
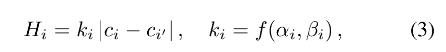
其中 c i c_i ci 和 c i ′ c_i^' ci′ 是渲染前第 i 个像素和第 i ′ i^' i′ 个像素的颜色。 k i k_i ki 是两个变量 α i , β i \\alpha_i, \\beta_i αi,βi 的函数,其中 α i \\alpha_i αi 的定义如公式(2)所示,而 β i \\beta_i βi 的定义如下:
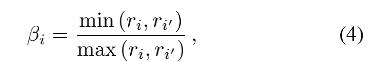
它表示两个像素中更小的和更大的模糊核半径的比例。。 k i k_i ki 随重新聚焦的视差、正在处理的像素和深度边界之间的最短距离而变化。 为清楚起见,我们假设 | c i − c i ′ c_i- c_i^' ci−ci′ | = 1 并在图 5 的前两列中绘制 Hi 的图形。基于观察到 Hi 随着 α i , β i \\alpha_i, \\beta_i αi,βi 的增加而减小,我们启发式地重写了方程 2为:
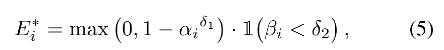
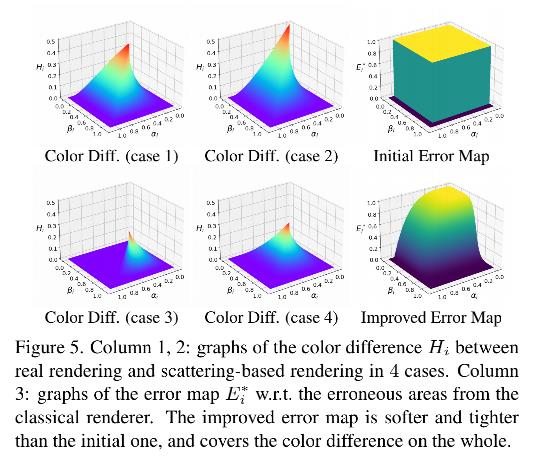
其中 δ 1 , δ 2 \\delta_1, \\delta_2 δ1,δ2 是两个超参数。当设置 δ 1 = ∞ , δ 2 = 1 \\delta_1=\\infty, \\delta_2=1 δ1=∞,δ2=1 的时候,该公式等于公式 2。请注意,在我们的实现中,我们将第二个指标函数项替换为平滑项,即 0.5 +0.5 tanh (10 ( δ 2 − β i \\delta_2 - \\beta_i δ2−βi))。 在比较了使用不同超参数训练的模型(在补充材料中)之后,我们根据经验设置 δ1 = 4 和 δ2 = 2/3。我们在图 5 的最后一列还展示了初始 E i ∗ E^*_i Ei∗(等式 2)和改进后的 E i ∗ E^*_i Ei∗ 的图 (Eq. 5) 。注意,当 0 ≤ βi ≤ 1 时,如果 βi > 1,我们定义 E i ∗ E^*_i Ei∗ = 0。可以观察到改进后的 E i ∗ E^*_i Ei∗比最初的要更软更紧密,仍然覆盖了色差较大的区域。 另一个实际示例如图 6 所示。

3.2 神经渲染器和模型训练
为了处理在深度不连续处的渲染问题和解决模糊范围的限制问题,我们提出了一个包含两个子网络的神经渲染器:ARNet 和 IUNet(如图 7 所示)。为了简化神经渲染器的输入,我们基于公式 1 定义了一个带符号的散焦图(defocus map)S:
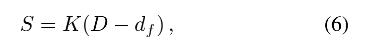
它对深度关系和空间变化模糊半径的信息进行编码。 为了匹配经典渲染器中的伽马校正,我们使用一个填充了归一化伽马值的贴图作为附加输入。
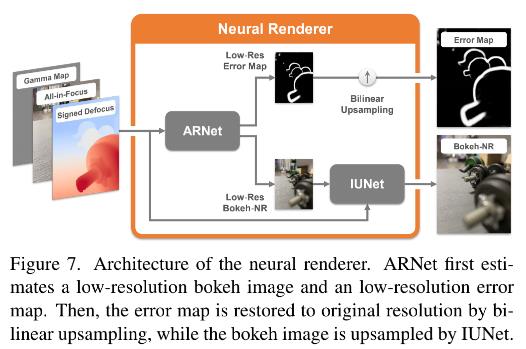
ARNet自适应调整输入图片的大小,然后输出一个误差图和低分辨率的虚化图 B n r l r B_nr^lr Bnrlr,如图 8 所示。自适应调整层包含两个步骤,第一步是计算下采样的比例因子:
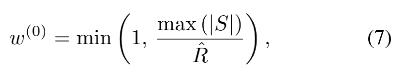
其中max(|S|) 表示整张图的最大模糊半径。 R ^ \\hatR R^ 则是我们给网络设置的最大模糊半径。第二步则是对所有图片进行下采样然后根据 w ( 0 ) w^(0) w(0) 的比例减小带符号散焦图的数值范围。网络的中间部分是轻量级和可替换的。 在这项工作中,我们使用与 DeepFocus(快速版本)[35] 相同的架构。

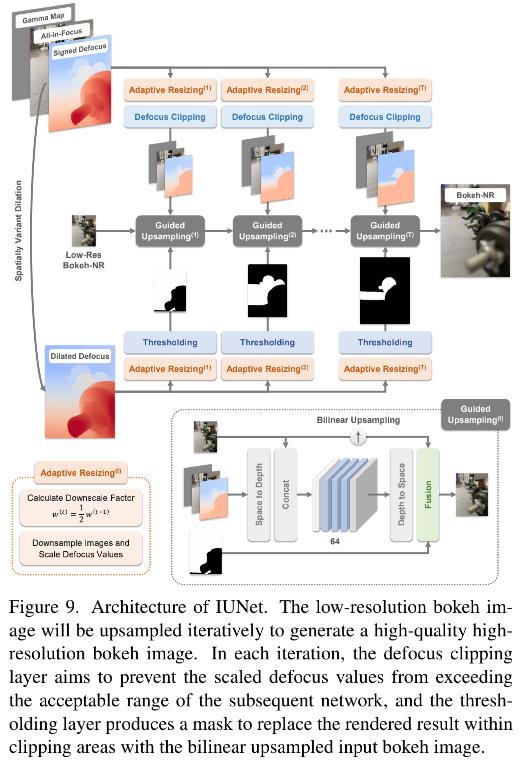
IUNet 对低分辨率的虚化图 B n r l r B_nr^lr Bnrlr 采用 2 作为比例因子进行迭代地上采样到原始输入分辨率,如图 9 所示。为了避免直接双线性上采样引起的对焦区域周围的模糊性,我们使用原始的高分辨率输入作为指导图。在每次迭代中,将其大小调整为输入虚化图像分辨率的两倍。 为了匹配迭代过程中不断增加的模糊大小,我们还需要动态调整散焦图的值。 具体来说,我们再次使用自适应调整层,每次迭代的缩小因子 t 设置为
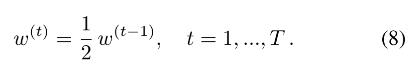
然而,随着迭代的进行,缩放后的散焦值可能会超出神经网络的可接受范围[ − R ^ , R ^ -\\hatR, \\hatR −R^,R^]。幸运的是,直接双线性上采样引起的模糊对于虚化模糊量大的区域并不明显。因此,我们可以只细化散焦值在该范围内的区域。为此,我们首先对超出范围的散焦值进行clip,以确保后续网络可以正常工作而不会崩溃。然后,我们对扩张的散焦图 S d S^d Sd 进行阈值化以生成一个蒙版,该蒙版表示没有散焦裁剪的有效渲染区域。在这些区域中,我们使用网络的输出,而对于其余区域,我们使用双线性上采样后的输入散景图像。在这里,我们使用 S d S^d Sd 代替 S,因为散焦裁剪造成的负面影响会在渲染过程中扩散。 S d S^d Sd的详细计算在补充材料中。总体而言,随着迭代次数的增加,虚化图像的分辨率会更高,但网络细化的有效区域会变小。换句话说,焦平面附近的区域将被细化更多次。
最后,遵循 alpha 融合[19,36],我们采用预测的误差图 E 来融合经典渲染器的虚化结果 B c r B_cr Bcr和神经渲染器的虚化结果 B n r B_nr Bnr:

损失函数。我们分别训练 ARNet 和 IUNet。当训练 ARNet 的时候,自适应调整层并不会使用。B 是 B c r B_cr Bcr 和 B n r l r B_nr^lr Bnrlr以上是关于BokehMe: When Neural Rendering Meets Classical Rendering的主要内容,如果未能解决你的问题,请参考以下文章