攻不下dfs不参加比赛

Posted 2023-02-02 肥学

标题

• 为什么练dfs
• 题目
• 总结

为什么练dfs

相信学过数据结构的朋友都知道dfs（深度优先搜索）是里面相当重要的一种搜索算法，可能直接说大家感受不到有条件的大家可以去看看一些算法比赛。这些比赛中每一届或多或少都会牵扯到dfs，可能提到dfs大家都知道但是我们为了避免眼高手低有的东西看着自己很明白就是写不出来。为了避免这种尴尬我们这几天乘着这个活动练练，好了我们话不多说开始肥学。

题目

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

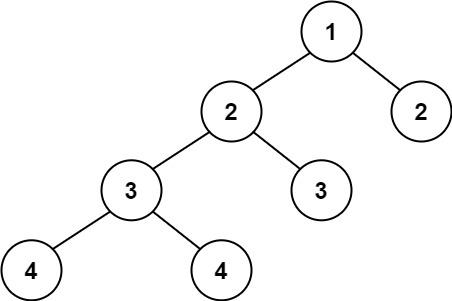
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

思路：其实这次是上次找最大深度的一个延申，也就是有一个函数可以计算每个节点左右子树的高度然后有了计算节点高度的函数，即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 11，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。

/**
 * Definition for a binary tree node.
 * public class TreeNode 
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() 
 *     TreeNode(int val)  this.val = val; 
 *     TreeNode(int val, TreeNode left, TreeNode right) 
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     
 * 
 */
class Solution 
    public boolean isBalanced(TreeNode root) 
        if (root == null) 
            return true;
         else 
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        
    

    public int height(TreeNode root) //计算每个节点的高度
        if (root == null) 
            return 0;
         else 
            return Math.max(height(root.left), height(root.right)) + 1;
        
    

总结

时间复杂度：O(n^2)，其中 nn 是二叉树中的节点个数。
最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 O(n)。

空间复杂度：O(n)，其中 nn 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 nn。